Контрольна робота з теми "Площі многокутників", 8 клас
Про матеріал
Контрольна робота складаєтся з 2х варіантів, в кожному з яких по 5 завдань на перевірку вмінь знаходити площі трикутника, паралелограма, ромба і трапеції. Перегляд файлу
1 варіант
- Знайти площу паралелограма, сторона якого дорівнює 12 см, а висота, проведена до неї, – 7 см.
- Знайти площу рівнобедреного трикутника, бічна сторона якого дорівнює 15 см, а а висота, проведена до основи, – 9 см.
-
Знайти площу ромба, сторона якого дорівнює
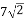 см, а один з кутів – 135.
см, а один з кутів – 135.
- Знайти площу паралелограма, сторони якого дорівнюють 25 см і 7 см, а одна з діагоналей перпендикулярна до його сторони.
- Знайти площу трапеції, основи якої дорівнюють 7 см і 9 см, а бічна сторона довжиною 6 см утворює з більшою основою кут 45.
1 варіант
- Знайти площу паралелограма, сторона якого дорівнює 12 см, а висота, проведена до неї, – 7 см.
- Знайти площу рівнобедреного трикутника, бічна сторона якого дорівнює 15 см, а а висота, проведена до основи, – 9 см.
-
Знайти площу ромба, сторона якого дорівнює
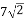 см, а один з кутів – 135.
см, а один з кутів – 135.
- Знайти площу паралелограма, сторони якого дорівнюють 25 см і 7 см, а одна з діагоналей перпендикулярна до його сторони.
- Знайти площу трапеції, основи якої дорівнюють 7 см і 9 см, а бічна сторона довжиною 6 см утворює з більшою основою кут 45.
1 варіант
- Знайти площу паралелограма, сторона якого дорівнює 12 см, а висота, проведена до неї, – 7 см.
- Знайти площу рівнобедреного трикутника, бічна сторона якого дорівнює 15 см, а а висота, проведена до основи, – 9 см.
-
Знайти площу ромба, сторона якого дорівнює
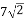 см, а один з кутів – 135.
см, а один з кутів – 135.
- Знайти площу паралелограма, сторони якого дорівнюють 25 см і 7 см, а одна з діагоналей перпендикулярна до його сторони.
- Знайти площу трапеції, основи якої дорівнюють 7 см і 9 см, а бічна сторона довжиною 6 см утворює з більшою основою кут 45.
2 варіант
- Основи трапеції дорівнюють 8 см і 4 см, а її висота – 3 см. Знайти площу трапеції.
- Основа рівнобедреного трикутника дорівнює 16 см, а бічна сторона – 17 см. Знайти площу трикутника.
-
Знайти площу ромба, сторона якого дорівнює
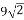 см, а один з кутів – 45.
см, а один з кутів – 45.
- Кут між висотами паралелограма, проведеними з вершини тупого кута, дорівнює 60. Знайти площу паралелограма, якщо його сторони 8 см і 14 см.
-
Знайти площу трапеції, основи якої дорівнюють 8 см і 14 см, а діагональ довжиною
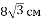 утворює з більшою основою кут 30.
утворює з більшою основою кут 30.
2 варіант
- Основи трапеції дорівнюють 8 см і 4 см, а її висота – 3 см. Знайти площу трапеції.
- Основа рівнобедреного трикутника дорівнює 16 см, а бічна сторона – 17 см. Знайти площу трикутника.
-
Знайти площу ромба, сторона якого дорівнює
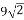 см, а один з кутів – 45.
см, а один з кутів – 45.
- Кут між висотами паралелограма, проведеними з вершини тупого кута, дорівнює 60. Знайти площу паралелограма, якщо його сторони 8 см і 14 см.
-
Знайти площу трапеції, основи якої дорівнюють 8 см і 14 см, а діагональ довжиною
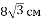 утворює з більшою основою кут 30.
утворює з більшою основою кут 30.
2 варіант
- Основи трапеції дорівнюють 8 см і 4 см, а її висота – 3 см. Знайти площу трапеції.
- Основа рівнобедреного трикутника дорівнює 16 см, а бічна сторона – 17 см. Знайти площу трикутника.
-
Знайти площу ромба, сторона якого дорівнює
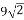 см, а один з кутів – 45.
см, а один з кутів – 45.
- Кут між висотами паралелограма, проведеними з вершини тупого кута, дорівнює 60. Знайти площу паралелограма, якщо його сторони 8 см і 14 см.
-
Знайти площу трапеції, основи якої дорівнюють 8 см і 14 см, а діагональ довжиною
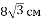 утворює з більшою основою кут 30.
утворює з більшою основою кут 30.
Середня оцінка розробки
Оцінки та відгуки
-
Дякую
docx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
