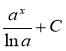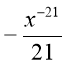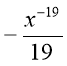Тема уроку: Правила знаходження первісних.

Мета уроку: повторення таблиці первісних;  формування знань учнів про правила знаходження первісних, формування умінь у знаходженні первісних для даних функцій, користуючись правилами знаходження первісних; розвивати навики самоконтролю,інтерес до предмету, пам'ять, увагу; виховувати волю та наполегливість для досягнення кінцевого результату при виконанні завдань, самостійність, уміння розраховувати час.

Очікувані результати: учні повинні вміти знаходити первісні за допомогою таблиці первісних  та правил знаходження первісних; виділяти первісну, яка задовольняє задану умову.

Обладнання: мультимедійний комплект; ноутбук, екран.

Наочність: презентації Power Point.

Тип уроку:  засвоєння нових знань ( урок з використанням комп’ютера та інтерактивних технологій навчання).

 

Хід уроку

1. Організаційний момент.
2. Актуалізація опорних знань учнів:

 

Доброго дня, шановні учні!

          Я вас вітаю!!!  Сьогодні ми розглянемо нову тему.

Для того,щоб згадати про що йшла мова на попередніх уроках - я пропоную розглянути ребус.  Яке ж слово тут  заблукало? Чекаю відповіді!!!

 

 

 

 

 

 

 

 

 

 

 

 

 

3.    Мотивація начальної діяльності

 

Знайти первісні  F(x) для функції  у= f(x)

Ваше завдання: розв’язати та знайти правильну відповідь (заштрихувати правильну відповідь жовтим кольором);

Записати  у відповідь ту букву,яка відповідає вірному розв’язку (набір відповідей знаходиться у табличках).

 

 

 

1) f(x)=х^п, n≠-1

	A	К	Я	Г
1	nxn+1  +C	nxn-1  +C

 

 

 

 

2) f(x)=Cosx

	A	Л	В	Н
2	-  Cosx +C	- Sinx+C	tgx +C	Sinx+C

 

 

 

3) f(x)=

	Н	С	В	Г
3	LnIxI+C	Ln +C	+C	- LnIxI+C

4 ) f(x)=

	С	А	В	Г
4	–ctgx + C	tgx+C	-tgx+C	sinх

 

5) f(x)= e^x    

	А	Б	В	Г
5	ax +C	-ex +C	ex +C	-ax +C

6) f(x)= 

	Ш	Б	У	Г
6	+C	+C	2+C	-2+C

7) f(x)=  a^x       

	A	Л	В	Р
7	ax  Lna+C	LnIxI+C	ах  +C

8) f(x)= k(стала)

	С	Б	Г	Д
8	0+c	1+c	kx+c	X+c

 

9) f(x)= sin х

	Е	Б	В	А
9	-  Cosx +c	-sin х+c	Cosx +c	tgx+C

 

10)f (x)=8 х⁷

	A	М	Т	П
10	56x6	+C	X8+C	+C

 

11) )f (x)=x^-20

	Я	Б	Н	Г
11	-20x-19+C	+C	+C	+C

 

12)Для функції  f(x)= 5 e^x  знайти первісну F, графік якої проходить через точку A(0;0).

	A	і	у	Г
12	5 ex  +2	5 ex  + с	5 ex  +5	5 ex  + С

 

ВІДПОВІДЬ: інтегрування

                        яннавургетні

 

 

 

 

4. Сприймання і осмислення нового матеріалу. (матеріал подається у вигляді презентації).  (додаток презентація1 «Правила знаходження первісних»)

Нагадаємо, що операція знаходження похідної для заданої функції називається диференціюванням. Обернена операція зна­ходження первісних для даної функції називається інтегруван­ням.

Правила інтегрування можна також одержати за допомогою правил диференціювання.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Висновок

Ми опрацювали новий матеріал. Записали основні формули в зошит.

Розглянули приклади, записані після  кожного правила. Зробили короткий запис цих вправ в зошит.

Зараз ви застосуєте вивчені правила до розв'язування вправ. Ви отримаєте для закріплення вправи, які необхідно розв'язати самостійно.

 

5. Формування умінь знаходити первісні для функцій, користуючись правилами знаходження первісних (додаток 2 тести)

1. Знайдіть загальний вигляд первісних F для функцій  f. (використовуйте правила 1-3).

Розв'язання цих вправ записуйте в зошиті.

 Результати розв'язку шукайте у листі з відповідями: кожному прикладу відповідає певна відповідь. Відповіді ви мусите  записати у вигляді послідовності чисел. Я повинна отримати закодований результат. Приклад:68451…

Бажаю успіхів в нелегкій справі: підніматися на  вершину Знань!

 

а) f(x) = 2х⁵ - 5х²;    (1б)

б) f(x)= + ;      (2б)

в) f(x) = sin4;       (1б)

г) f(x)=(2x-5)⁷                (2б)                                 

д) f(x) = е^4х+7                  (1 б)

е) f(x) =10^3х-1 - 2cos 6x;      (2 б)

ж)f(x) = 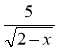+        (3 б)

Відповіді:1) F (x)=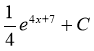;  2)F (x)= -10 ;

3);      4) F (x)= -10 ;

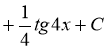5) F (x)=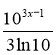- 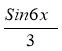+С;    6) F (x)= 3ln |x|- +C;

7) F (x)=4e^x+7 + с;    8) F (x)= -;

9) F (x)= -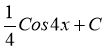;   10) F (x)=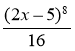+С;

11) F (x)=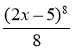+С;    12) F (x)=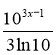+ +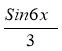С;  

13) .

а)3;  б)6;  в)9;  г)10;  д)1;  е)5;  є)4

Відповідь:3 6 9 10 1 5 4

 

6. Підведення підсумків уроку.

7. Домашнє завдання: п.25-правила,№25.6; №25.7