Завдання для практичної роботи: Аналітична геометрія (пряма лінія на площині)
АНАЛІТИЧНА ГЕОМЕТРІЯ НА ПЛОЩИНІ
Практичне заняття
Застосування рівнянь прямих до дослідження їх взаємного розташування, знаходження кута між ними. Застосування властивостей кривих другого порядку до розв’язування прикладних задач.
Мета. Знати рівняння прямої у різних формах, еліпса, гіперболи, параболи, вміти застосовувати їх до розв’язування задач, будувати криві другого порядку за їх рівняннями та визначати їх властивості.
Теоретичні відомості
|
Відстань
Координати точки
При
|
Завдання 1
-
Визначити відстань між точками
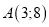 і
і 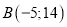 .
.
-
Довести, що трикутник з вершинами
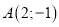 ,
, 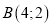 ,
, 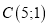 рівнобедрений.
рівнобедрений.
-
Дано вершини трикутника
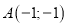 ,
, 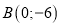 і
і 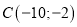 . Знайти довжину медіани, проведеної з вершини А.
. Знайти довжину медіани, проведеної з вершини А.
-
Серединою відрізка
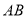 є точка
є точка 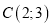 . Визначити координати точки
. Визначити координати точки 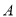 , якщо
, якщо 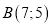 .
.
Теоретичні відомості
Рівняння прямої
Якщо відомі кутові коефіцієнти двох прямих Умовою паралельності двох прямих є рівність їх кутових коефіцієнтів
Умовою перпендикулярності двох прямих є співвідношення
Відстань від точки
|
Завдання 8
Дано координати вершин трикутника ![]() . Знайти:
. Знайти:
- довжину сторони АВ;
- рівняння сторін АВ іВС;
- внутрішній кут В;
- рівняння медіани АЕ;
- рівняння і довжину висоти СD;
-
рівняння прямої, яка проходить через точку
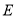 паралельно стороні
паралельно стороні 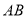 .
.
1) ![]()
2)![]()


про публікацію авторської розробки
Додати розробку
