Презентація "Визначений інтеграл. Формула Ньютона-Лейбніца"
Про матеріал
Математика, 11 клас, рівень стандарт
Презентація містить теоретичний матеріал, історичні довідки про вчених та літературне обрамлення. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку







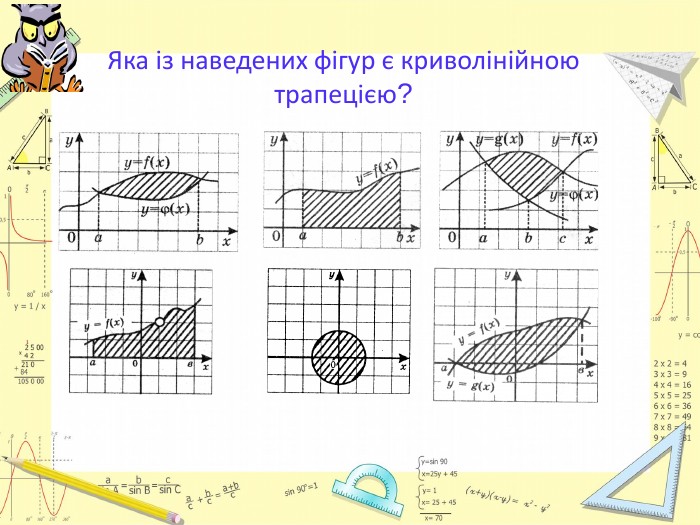
![Означення: Криволінійною трапецією називається фігура, обмежена графіком неперервної функції y=f(x), яка не змінює знак на відрізку[a; b], прямими x=a, x=b і відрізком [a; b]. Криволінійна трапеція Означення: Криволінійною трапецією називається фігура, обмежена графіком неперервної функції y=f(x), яка не змінює знак на відрізку[a; b], прямими x=a, x=b і відрізком [a; b]. Криволінійна трапеція](/uploads/files/143840/272687/296638_images/8.jpg)
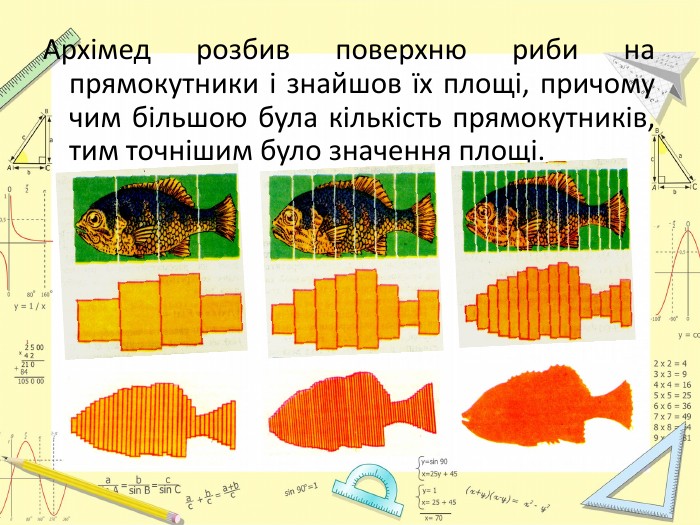
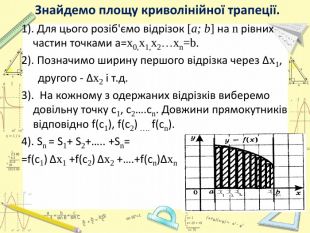
![Знайдемо площу криволінійної трапеції. 1). Для цього розіб'ємо відрізок [a; b] на n рівних частин точками а=x0,x1,x2…xn=b. 2). Позначимо ширину першого відрізка через ∆x1, другого - ∆x2 і т.д. 3). На кожному з одержаних відрізків виберемо довільну точку с1, с2….сn. Довжини прямокутників відповідно f(с1), f(с2) …. f(сn).4). Sn = S1+ S2+….. +Sn= =f(с1) ∆x1 +f(с2) ∆x2 +….+f(сn)∆xn Знайдемо площу криволінійної трапеції. 1). Для цього розіб'ємо відрізок [a; b] на n рівних частин точками а=x0,x1,x2…xn=b. 2). Позначимо ширину першого відрізка через ∆x1, другого - ∆x2 і т.д. 3). На кожному з одержаних відрізків виберемо довільну точку с1, с2….сn. Довжини прямокутників відповідно f(с1), f(с2) …. f(сn).4). Sn = S1+ S2+….. +Sn= =f(с1) ∆x1 +f(с2) ∆x2 +….+f(сn)∆xn](/uploads/files/143840/272687/296638_images/10.jpg)

![Формула Ньютона - Лейбніца Це і є формула Ньютона – Лейбніца, яка показує, що значення визначеного інтеграла на відрізку [a; b] дорівнює різниці значень первісної підінтегральної функції, коли x=b i х=a. Різницю F(b) - F(a) позначають . Тому попередню рівність можна записати так: Формула Ньютона - Лейбніца Це і є формула Ньютона – Лейбніца, яка показує, що значення визначеного інтеграла на відрізку [a; b] дорівнює різниці значень первісної підінтегральної функції, коли x=b i х=a. Різницю F(b) - F(a) позначають . Тому попередню рівність можна записати так:](/uploads/files/143840/272687/296638_images/12.jpg)
![Обчислення площ плоских фігур. Отже, , якщо f(x) ≠0 для всіх x є [а;b], являє собою площу криволінійної трапеції обмеженої лініями: у = f(x), x = а, х = b, y = 0. Це – геометричний зміст інтегралу. Обчислення площ плоских фігур. Отже, , якщо f(x) ≠0 для всіх x є [а;b], являє собою площу криволінійної трапеції обмеженої лініями: у = f(x), x = а, х = b, y = 0. Це – геометричний зміст інтегралу.](/uploads/files/143840/272687/296638_images/13.jpg)


















-

Харченко Ірина Вікторівна
16.01.2024 в 21:33
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Корнієнко Світлана Анатоліївна
30.11.2023 в 12:14
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Новомлинська Дар'я Сергіївна
27.11.2023 в 18:53
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Пузик Олена
24.04.2023 в 08:59
Дякую за презентацію, за оригінальну подачу матеріалу
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ковтун Ганна Олександрівна
31.01.2023 в 22:48
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Самойленко Наталя Миколаївна
17.11.2022 в 12:43
Дякую за чудову, оригінальну презентацію.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Nevirkovets Larysa
10.11.2022 в 18:42
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 4 відгука