Урок+ Презентація "Квадратична функція"

Тема: Квадратична  функція, її  властивості  і  графік

Мета:            навчальна: узагальнення  та  закріплення  знань  учнів; відпрацювання  навичок  розв’язання тестових  завдань; відпрацювання  алгоритму  побудови графіка  квадратичної  функціївиявлення  рівня  сформованості знань, умінь  та  навичок  учнів  з теми;                            розвиваюча: сприяти  розвитку  умінь  виявляти  суттєві  властивості       квадратичної  функції, порівнювати, узагальнювати; розвивати комунікативні зв’язки, інформаційну  грамотність, логіку;

         виховна: стимулювати  учнів до  самооцінки  освітньої  діяльності

через  самопізнання, самовизначення  та  самореалізацію.

        Завдання уроку: повторити властивості  квадратичної  функції,                                систематизувати  знання з  побудови графіка  квадратичної  функції; здійснити  контроль  та оцінити  знання  учнів; застосувати методи  самоконтролю та взаємоконтролю; побудувати  графіки  даної              функції і  розглянути  їхні              властивості.

       Очікувані  результати: учні  повинні  виявити   рівень  сформованості  знань, компетентність  під  час побудови  графіків  квадратичної функції, виявлення властивостей квадратичної функції,  розв’язання тестових  завдань  з теми.

       Тип  уроку: узагальнення  та  систематизація  вивченого  матеріалу.

       Вид уроку: урок-презентація.

       Обладнання: дошка, зошити, проектор, презентація, дидактичний  матеріал, роздавальний  матеріал(картки).

                                          Хід  уроку

1. Організаційний  етап.

      Привітання, створення  сприятливих  умов  до  проведення  уроку, позитивного  настрою  в  класі.

      Слово вчителя.                                                                                                                                                                                                                                                                                               Доброго  ранку,    діти!   Я  рада   вас   бачити    сьогодні   на   уроці   і    дуже  сподіваюсь на  колективну  плідну  роботу.   Є хороше  прислів’я   «Доки не впріти, доти не вміти».   Особливо  воно  стосується  математики, щоб добре   засвоїти  та  систематизувати  вивчений  матеріал.

       Отже, починаємо  працювати. Відкрийте  зошити, запишіть  дату  і  сьогоднішню тему уроку (слайд1) «Квадратична функція, її  властивості і  графік» (Далі  вчитель  дає  інформацію  про мету та  хід  уроку, диференційовану  роботу  та  оцінювання  ЗУН  учнів. Ознайомлення  з  листом  оцінювання  та  його  заповнення) (додаток 1)

      2.  Мотивація уроку.

      Слово  вчителя.

      Іноді говорять, алгебра  тримається  на  чотирьох  китах : число, рівняння, тотожність  і  функція. (слайд 2)

      Дайте  визначення  функції.    

      Учень. Якщо кожному значенню змінної х з деякої множини відповідає єдине значення змінної у, то таку залежність називають функціональною залежністю, або функцією. При цьому змінну х називають незалежною змінною або аргументом, змінну у - залежною змінною або функцією від аргументу. (слайд 3)

     Учитель. Правильна  відповідь. Сьогодні  наш  урок - урок-презентація. Перед  вами   (слайд 4-7)  зображені  автомобільна  фара, проектор, телескоп, параболічна  антена.  Як  усі  ці  предмети  пов’язані  з  квадратичною  функцією? Щоб  дізнатися  відповіді, треба відпрацювати  усі  представлені  номінації нашого уроку. Результати  не  забувайте  вносити  до  листа  оцінювання.

3. Актуалізація уроку.

Номінація №1 «Паспорт  квадратичної  функції». (слайд 8)

     По  ключовим  словам  треба  охарактеризувати  квадратичну  функцію.

Питання 1 до  учнів. Дайте  означення  квадратичної  функції. (слайд 9)

Відповідь  учня. Функція виду у = ах²+bх+с, де а, b, c –  деякі  числа, а≠0, 

х –  незалежна змінна, називається квадратичною функцією.

Питання 2 до  учнів. Як  називається  графік  квадратичної  функції? Наведіть приклади. (слайд 10)

Відповідь  учня.    Графіком квадратичної функції  є парабола,  вітки якої  направлені   вгору (якщо а>0)  або   вниз (якщо  а<0).

Питання 3 до  учнів. Як  обчислити  координати  вершини  параболи?  (слайд 11)

Відповідь  учня.  Для того, щоб знайти вершину параболи, необхідно скористатись наступними формулами

 (m;n) – координати вершини параболи               m= - n= -

Питання 4 до  учнів.   Вісь  симетрії  параболи та її рівняння. (слайд 12)

Відповідь  учня.   Так як квадратична функція парна функція, то її графік буде симетричний відносно вісі симетрії. Вісь симетрії проходить через вершину параболи. Рівняння      у = m

Питання 5 до  учнів. Як залежать нулі функції від дискримінанта?

                                        (слайд 13-16)

Відповідь  учня. Якщо D>0 ,то ми будемо мати 2 дійсних-різних корені

 

Якщо D=0, то ми матимемо 2 дійсних-рівних корені

 

Якщо D<0, то дійсних коренів квадратний тричлен не матиме,  графік функції не перетинає вісь 0х в жодній точці

Питання 6 до  учнів. Назвіть  властивості  квадратичної  функції   

                         у = -х²-6х-8, користуючись  даними. (слайд 17,18)

Відповідь  учня.  у>0 на  проміжку  (-4;-2);

                               у<0 на проміжку  (-∞;-4);(-2;+∞);

                              функція  зростає  на   проміжку (-∞;-3];

                              функція   спадає   на   проміжку [-3;+∞);

                              найбільше значення функції  дорівнює 1, при х=-3 

     4.  Застосування знань, умінь і навичок.         

Номінація №2  «Крізь  історію  до  знань». (слайд 19)

         Цікаво  дізнатися, з  чого  все  почалося?  Де  історичне  коріння  квадратичної  функції? Діти, зараз  ви  отримаєте  картки  із  завданнями (додаток 2), які  ви  повинні  розв’язати. Одне  із  завдань  історичне. З початку відповідаємо на перше питання в картці. Потім учні з картками 1 та 2 виходять до дошки, виконують друге завдання і т. д.

Картка №1

1. Цей  науковець  довив, що  якщо  швидкість  тіла 11,16 км/сек. (друга  космічна  швидкість), то його траєкторією є парабола. (Ньютон) (слайд 20,21)

2. При  яких значеннях а функція y=ax²+5 має  нулі? (слайд 28)  

    а) а>0;                         б) а≠0;                   в) а<0                           

Картка №2

1. Який науковець, інженер і механік, за давне грецькою легендою, з допомогою величезних дзеркал спалив римські кораблі? (Архімед)

 (слайд 22,23)

2. Знайдіть   проміжок спадання функції  y = (x-2)²+2 (слайд 28) 

    а) (- ∞; 1,5];                  б) (-∞ ; 3];          в) (-∞ ; 2)              

Картка №3

1. У 3 ст.  до н. е. він  вперше назвав цю криву параболою. (Аполлоній) (слайд 24,25)

2. Записати рівняння  параболи, яку  отримали з параболи  y=x² із   зсувом  вздовж вісі ОХ на 2 одиниці вліво  і  вздовж вісі  ОУ на 1 одиницю  вниз. (слайд 29)             

 а) y = (x-2)²-1;             б) у = (x+2)²-1;           в) y = (x-2)²+1         

Картка №4

1. Великий астроном, механік  і фізик довив, що траєкторією руху  снаряда  є парабола. (Галілей) (слайд 26,27)

2. Установіть, яка з точок А(1;-5),  В(4;9), С(-4;11) належить  графіку функції

 y=3(x-1)²-5   (слайд 29)                  А(1;-5)

Картка №5

1. Великий астроном, механік  і фізик довив, що траєкторією руху  снаряда  є парабола. (Галілей) (слайд 26,27)

2. Графіком квадратичної функції  є  парабола  з вершиною  в точці  А(0;1),    вітки направлені  вгору. Задайте цю функцію формулою.               (слайд 30)                           

  а) y = -x²+1;               б) y = x²-1;                    в) y = x²+1            

Картка №6

1. У 3 ст.  до н. е. він  вперше назвав цю криву параболою. (Аполлоній) (слайд 24,25)

2. Знайдіть   проміжок зростання функції y = (x-2)²+2    (слайд 30)

   а) (2;+∞);                  б) (-∞ ; 3];                         в) (-∞ ; 2)             

Картка №7

1. Який науковець, інженер і механік, за давне грецькою легендою, з допомогою величезних дзеркал спалив римські кораблі? (Архімед)

(слайд 22,23)

2. При  яких значеннях а функція y=ax²-6 не має нулів? (слайд 31)

 а) а>0;                            б) а≠0;                             в) а<0           

Картка №8

1. . Цей  науковець  довив, що  якщо  швидкість  тіла 11,16 км/сек. (друга  космічна  швидкість), то його траєкторією є парабола. (Ньютон) (слайд 20,21)

2. З’ясувати, скільки нулів має функція  y = -2x²+8x-6?  (слайд 31)

                      2 нуля

       Не  забувайте  заповнювати  лист  оцінювання і перевіряти правильні відповіді.

Номінація  №3 «Книга  книгою, а  мозком  рухай». (слайд 32)

Форма  проведення  тестова. Будьте уважні при виконанні завдань.

(Учитель роздає картки з тестами) (додаток 3,4,5)

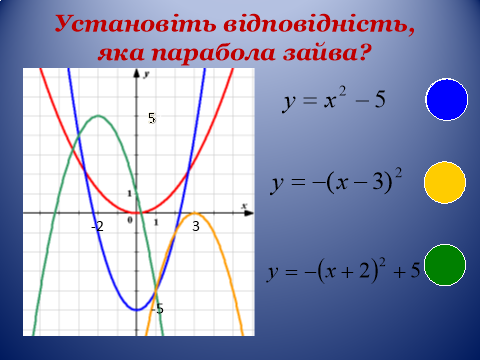
1) Установіть  відповідність:  якій  функції  відповідає  графік? Яка  парабола  зайва? (додаток 3)  (слайд 33)

2) Для  кожної з  функцій, графіки  яких  зображені, виберіть  відповідну  умову  та  зробіть  позначку  «+». (додаток 4,5)  (слайд 34,35)

Виконайте  взаємоперевірку, звертаючись  до  відповідей  на  слайдах. Позначте  кількість  зароблених  балів  у  листі  оцінювання.

Номінація № 4 «Графомани». (слайд 36)

        Кожен  з  учнів  одержує  своє  власне  завдання, будує  графік  функції, визначає  її  властивості. У кінці уроку я зберу зошити і перевірю виконання ваших робіт. А потім результат внесу до листів оцінювання.

у = x²+2;  у = (х-3)²+8;    у = (х-9)²;   у = -х²;  у = -(х+6)²+5;    у = -(х-10)²-1;    

   у = - x²-3;      у = х²  (додаток 6) (слайд 37)

Номінація № 5 «Від  теорії  до  практики  в житті».  (слайд 38)

      Ви на минулому уроці отримали  завдання  зробити  коротку  доповідь  про  властивості  параболи, про   їх  використання  в прожекторах, ліхтарях,  локаторах, телескопах. Світло  автомобільних  фар  також  нагадує  параболу.

Це  і  буде  відповіддю  на  поставлене  питання  на  початку  уроку.

      Хто підготував доповідь в друковому  варіанті здайте на перевірку, той отримає бали у номінації №5. Бали я поставлю вам у листі оцінювання.

         5. Підсумки  уроку.

        Слово  вчителя.

      Нарешті  можна  підвести  підсумки  нашої  роботи. Протягом  уроку  ви  виявили  задовільний  рівень  сформованості  знань, компетентність  під  час побудови  графіків  квадратичної               функції, виявлення  властивостей  квадратичної  функції,  розв’язання тестових  завдань  з теми.

Перевірте, будь  ласка, чи   заповнили ви свої  листи  оцінювання і здайте разом з зошитами. На наступному уроці я оголошу ваші результати.

      Ми досягли поставленої  мети  і тепер  ви  готові до  контрольної   роботи.

      6. Рефлексія.

Слово  вчителя. 

      Парабола  має цікаві  властивості, які  широко використовуються в техніці. На вісі симетрії параболи є  точка, яку називають  фокусом параболи. У параболи y=x² фокусом є точка  з координатами (0;). Якщо  в точці знаходиться джерело світла, то всі відображені від  параболи  промені йдуть паралельно вісі  параболи. Якщо  направити  на параболу пучок світлових променів, паралельних вісі симетрії, то після відображення  від  цієї   параболи, усі промені  пройдуть  через фокус.

     Ці  властивості використовуються  при  виготовленні  прожекторів, ліхтарів, локаторів, фар машин. При створенні таких  технічних  приладів  використовується параболоїд  обертання. Поверхню  такого параболоїда можна отримати, якщо параболу обертати  навколо  її  вісі.

       Пропоную вам переглянути коротке відео.

      7. Домашнє  завдання. (слайд 39) (творчого  характеру) з  коментуванням  учителя.

        Скласти  картки  з  цікавими  задачами  з  даної  теми.

       Дякую  за позитивний  настрій  та  відповідальне  ставлення  до  роботи  в  колективі. Бажаю  вам  і  надалі  успіхів  у  навчанні. До  побачення, на  все  добре!(сайд 40)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТОК 1

                                              Лист  оцінювання                                   П.І.  учня    ___________________________________________

 

Номінація	Кількість  балів	Загальна кількість балів  за номінацію
№1	По  1 балу
№2	5  балів
№3	По  1 балу
№4	5  балів
№5	5  балів
УСЬОГО   БАЛІВ
ОЦІНКА

 

«10-12» - 20  і  більше  балів,

«7-9» - від  15 до 19 балів,

«4-6» - від  10 до 14 балів,

«1-3» - менше 10 балів

 

 

 

 

 

 

 

 

 

ДОДАТОК 2

 

Картка №1

1. Цей  науковець  довив, що  якщо  швидкість  тіла 11,16 км/сек. (друга  космічна  швидкість), то його траєкторією є парабола. 

2. При  яких значеннях а функція y=ax²+5 має  нулі?    

    а) а>0;                         б) а≠0;                      в) а0

Картка №2

1.               Який науковець, інженер і механік, за давне грецькою легендою, з допомогою величезних дзеркал спалив римські кораблі?  

2. Знайдіть   проміжок спадання функції  y = (x-2)²+2     

  а) (- ∞; 1,5];              б) (-∞; 3];                     в) (-∞; 2)              

Картка №3

1. У 3 ст.  до н. е. він  вперше назвав цю криву параболою.  

2. Записати рівняння  параболи, яку  отримали з параболи  y=x² із   зсувом  вздовж вісі ОХ на 2 одиниці вліво  і  вздовж вісі  ОУ на 1 одиницю  вниз.

 а) y = (x-2)²-1;                   б) у = (x+2)²-1;                                 в) y = (x-2)²+1         

Картка №4

1. Великий астроном, механік  і фізик довив, що траєкторією руху  снаряда  є парабола. 

2. Установіть, яка з точок А(1;-5),  В(4;9), С(-4;11) належить  графіку функції

 y=3(x-1)²-5    

Картка №5

1. Великий астроном, механік  і фізик довив, що траєкторією руху  снаряда  є парабола. (Галілей) (слайд 26,27)

2. Графіком квадратичної функції  є  парабола  з вершиною  в точці  А(0;1),    вітки направлені  вгору. Задайте цю функцію формулою.                                           

  а) y = -x²+1;               б) y = x²-1;              в) y=x²+1 

 

Картка №6

1. У 3 ст.  до н. е. він  вперше назвав цю криву параболою.  

2. Знайдіть   проміжок зростання функції y = (x-2)²+2     

а) (2;+ ∞);                       б) (-∞ ; 3];                               в) (-∞ ; 2)            

Картка №7

1. Який науковець, інженер і механік, за давне грецькою легендою, з допомогою величезних дзеркал спалив римські кораблі? 

2. При  яких значеннях а функція y=ax²-6 не має нулів?  

 а) а>0;                            б) а≠0;                            в) а<0

Картка №8

1. . Цей  науковець  довив, що  якщо  швидкість  тіла 11,16 км/сек. (друга  космічна  швидкість), то його траєкторією є парабола. 

2. З’ясувати, скільки нулів має функція  y = -2x²+8x-6?   

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТОК 3

 

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТОК 4

Тест №1

D>0;a<0
D<0;a>0
D<0;a<0
D=0;a>0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТОК 5

Тест №2

 

(-∞;∞)
(-1;0)
х≠-1
Нет значений х

 

 

 

 

 

 

 

 

 

 

 

ДОДАТОК 6

Графомани

у = x²+2;  

 

 у = (х-3)²+8;   

 

у = (х-9)²; 

 

 у = -х²;

 

  у = -(х+6)²+5;

 

  у = -(х-10)²-1;    

 

у = - x²-3;    

 

 у = х²