Урок.Презентація. "Перша і друга ознака рівності трикутників"
Про матеріал
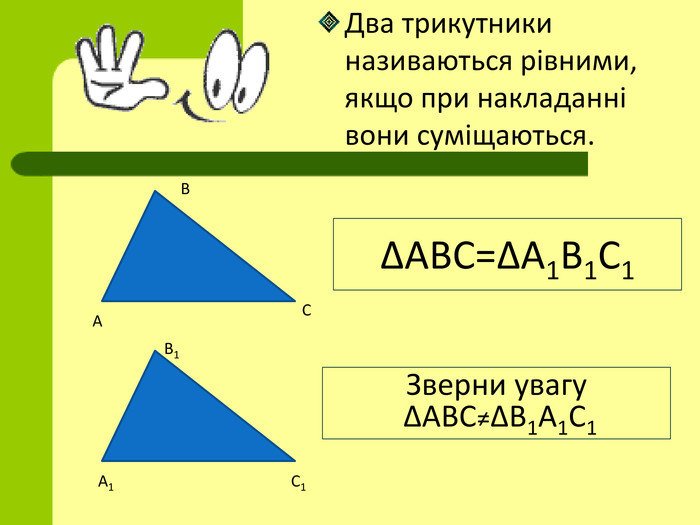
Тема: Перша і друга ознаки рівності трикутників.
Мета: формування в учнів знань про першу та другу ознаку рівності трикутників, формування уміння застосовувати першу і другу ознаку рівності трикутників до розв'язання задач.
Обладнання:інтерактивна дошка, Комп'ютерна презентація за програмою PоwerPoint, косинець,лінійка, транспортир, картки за правильну відповідь.
Тип уроку: Засвоєння новихзнань і вмінь.
Клас:7
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку

































-

Вигоднер Діана Ісаківна
09.11.2023 в 17:19
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Благонадєждіна Олена Євгенівна
19.10.2023 в 10:54
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Левадній Сергій Павлович
15.01.2023 в 15:51
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Худик Галина Михайлівна
30.11.2022 в 18:04
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Овчар Олена Анатоліївна
02.12.2021 в 07:49
Дякую)
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Svetlana
22.11.2021 в 20:29
Загальна:
4.0
Структурованість
4.0
Оригінальність викладу
4.0
Відповідність темі
4.0
-

Семенова Катерина Андріївна
10.11.2021 в 00:45
Презентація відмінна! Дуже дякую за таку роботу!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Миленина Татьяна
22.10.2019 в 22:42
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 5 відгуків