Урок+Презентація по темі "Розв’язування задач на прогресії, у тому числі прикладного змісту. "(алгебра 9 клас)

Методична розробка уроку алгебра 9 клас (за новою програмою )

Урок № 51

ТЕМА  УРОКУ.  Розв’язування  задач на прогресії, у тому числі  приклад-ного змісту.

МЕТА УРОКУ:

Навчальна: Узагальнити знання про прогресії, показати практичне застосування теми на прикладах задач із життя; переконати учнів у єдності теорії  і  практики.

Розвиваюча: розвивати вміння учнів створювати математичні моделі до розв'язування задач; пізнавальний інтерес учнів, уміння застосовувати  знання на практиці, сприяти творчому розвитку учнів.

Виховна: Виховувати  інтерес до предмету, старанність, відповідальність перед товаришами, вміння  працювати в групах,  взаємодіяти з однокласниками під  час підготовки до уроку. Виховувати почуття патріотизму та любові до рідної землі.

Обладнання:  комп’ютерна презентація, картки для кольорової рефлексії, мультимедійний проектор.

ТИП УРОКУ: урок  узагальнення і систематизації знань з теми «Прогресії».

Структура уроку:

Етап	Кількість хвилин
І. Організація класу до уроку	2 хв.
ІІ. Актуалізація опорних знань	5 хв.
ІІІ. Мотивація начальної діяльності	3 хв.
IV. Формулювання теми та мети уроку	2 хв.
V. Розв’язування задач прикладного змісту	10 хв.
VI. Фізкультхвилинка	2 хв.
VII. Розв’язування задач прикладного змісту	15 хв.
VIIІ. Підсумок уроку	5 хв.
ІX. Домашня робота	1 хв.

ХІД УРОКУ.
І. Організація класу до уроку
Перевірки наявності та готовності учнів до уроку. Створення позитивного настрою для проведення уроку.

Рада вас бачити. Нас чекає сьогодні багато роботи. Дуже хочу, аби наш урок був вдалим. Посміхніться та побажайте в думках своїм однокласникам, собі й мені успіхів. 

Для того, щоб впоратися на уроці з завданнями, будьте старанними і слухняними. (Слайд1)

          Девіз уроку:

Математику слід вивчати в школі ще й із тією метою, щоб одержані тут знання були достатні для звичайних потреб у житті!

М. І. Лобачевський

Ми починаємо урок, а на уроці ми…(Слайд 2)

Уважні!

Розумні!

Організовані!

Кмітливі!

Я  бажаю всім нам активності, плідної співпраці та досягнення поставленої мети. Тож давайте не гаяти часу.

ІІ. Актуалізація опорних знань

1. А повторення   основних  понять  теми ми здійснимо , розгадавши кросворд (Слайд 3)

Кросворд по темі «Послідовності»

1п

о

с

л

і

д

о

в

н

і

с

т

ь

2р

е

к

у

р

е

н

т

н

и

й

3п

о

п

е

р

е

д

н

і

й

4п

р

о

г

р

е

с

5ф

о

р

м

у

л

а

6ч

л

е

н

и

7с

п

а

д

н

а

8р

і

з

н

и

ц

я

9м

р

і

ї

По горизонталі:

1.Сукупність елементів, об’єднаних за певною ознакою і розміщених в           певному порядку.

2. Один із способів задання послідовностей.

3.Як називають член послідовності, що передує даному?

4.Рух вперед, поступове вдосконалення.

5.Правило, записане за допомогою рівності

6.Числа, що задають послідовність.

7. Вид послідовності.

8.Число d; або одна із арифметичних дій математики.

9.Думка про щось бажане.

По вертикалі: 1. Прогресії

2. На кожній парті завдання  «Математичне лото».(Слайд  4)

Повторення  вивченого  матеріалу теми  «Прогресії »пропоную зробити, склавши «математичне  лото». (Робота в парах)

 

Таблиці для математичного лото

 

Характеристична властивість арифметичної прогресії	Формула суми n-перших членів геометричної прогресії	Характеристична властивість геометричної прогресії
Формула n-го члена арифметичної прогресії	Формула cуми n-перших членів арифметичної прогресії	Формула n-го члена геометричної прогресії

 

 

 

 

Правильність виконання  перевіряємо за таблицею

 

Арифметична прогресія	Означення	Геометрична прогресія
=	Характеристична властивість	=
+d(n-1)	Формула n - ого члена	=
= , =	Формула суми  n перших членів	=

 

III. Мотивація навчальної діяльності

"Прогресія", "прогрес", "прогресивний" - слова одного кореня. Прогресія - це послідовність, побудована за таким законом, який дає змогу продовжувати її необмежено, тобто рухатися вперед. (Слайд 5)

Прогресія - явище без перебільшення, унікальне. Історія виникнення прогресії сягає глибини віків.

Підсумовуванням арифметичних і геометричних прогресій та складанням відповідних задач займалися багато любителів математики протягом багатьох століть. В розвиток теорії про прогресіях внесли вчені Архімед, Піфагор та його учні, французькі математики Леонард Фібоначчі і Баше де Мезіріак, німецькі математики М. Штіфель, Н. Шюке, і К. Гаусс.

Найдавнішою задачею на прогресії є задача про розподіл хліба, записана в Єгипетському папірусі Ринда, яка відноситься до III ст. до н. е.

Перші задачі на прогресії пов'язані із запитами господарського життя і суспільної практики (розподіл спадщини, одержання винагороди), із спостережень над явищами природи, з досліджень суспільно-економічних явищ. Так, у вавилонських текстах розповідається про те, що збільшення освітленої частини місячного диска протягом перших п'яти днів відбувається за законом геометричної прогресії зі знаменником 2, у наступні 10 днів - за законом арифметичної прогресії з різницею 16. Широкий інтерес вавілонян до астрономії робить зрозумілим виникнення цієї задачі.

Тривале життя прогресій зумовлене не тільки їх цікавими математичними властивостями, а й широким застосуванням в інших науках. На сьогоднішньому уроці ми і будемо розв’язувати задачі на прогресії, , які ілюструють використання прогресій за межами математики . А ще послухаємо ваші повідомлення, які ви готували вдома,  про застосування прогресій у різних сферах людської діяльності.

IV. Розв'язування задач прикладного змісту (Повідомлення учнів з розв’язуванням відповідних темі задач підручника Алгебра: підруч. для 9 кл. загальноосвіт. навч. Закладів/А.Г. Мерзляк, В.Б.Полонський, М.С. Якір. – Х. : Гімназія, 2017. – 272 с.)

1.              Прогресії в  історії.  Ми живемо в третьому тисячолітті, та історичні факти,  які відкриваються дослідниками, як відлуння древніх епох не втрачають своєї актуальності. Як не згадати  папірус Ринда, датований 2000 роком до н.е., як джерело цікавих задач. І в підручнику алгебри міститься ця задача.(Слайд 6)

Задача 17.17. (Стародавня єгипетська задача) Сто мір хліба треба розділити між п’ятьма людьми так, щоб другий отримав на стільки ж більше від першого, на скільки третій отримав більше за другого, четвертий більше за третього та п’ятий більше за четвертого. Окрім того, двоє перших повинні отримати в 7 разів менше, ніж троє останніх. Скільки треба дати кожному?(Учні записують розв’язання задачі в зошиті)

Розв’язання

Кількість хліба, яку отримав кожний з 5-ти людей, складає арифметичну прогресію, сума 5-ти членів якої за умовою дорівнює 100.  5

Маємо рівняння : ;

Перші двоє людей отримали ( ) мір  хліба, а троє останніх – () мір , що за умовою у 7 разів більше, ніж перших двоє.

Маємо рівняння:

7( )=

Складаємо систему:

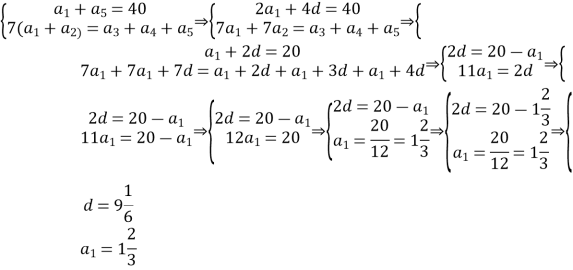
Отже, перша людина отримає мір хліба, друга – мір, третя –  20  мір, четверта - 29 мір, п’ята - 38.

Відповідь: 20, 2938

У цьому ж папірусі знаходимо задачу про нагородження винахідника шахів.  Наші історики знайшли, що цей папірус переписаний з того, який належав третьому тисячоліттю до н.е.

А ще дуже цікавою, на нашу думку, є легенда про Карла Фрідріха Гаусса, що придумав розв’язання задачі у віці 5 років.

   Задача. Про Карла Гауса. (Слайд 7)

Задача ця є непроста:

Ну як зробити швидко

Від одного і аж до ста

Усно  додати  числа?

П'ять перших пар ти поєднай

І ключ  до розв'язку  тримай!

1+100 = ? 2+99=? 3+98=?

4+97= ? 5+96 =?

Давно один мудрець сказав,

Отримать  результати, доволі просто,

Треба лиш початок  ряду і кінець

Залежністю   зв’язати.

 

Розв'язання:

1+100=101;   2+99=101; 3+98=101;   4+97=101; 5+96=101...

Таких сум є 50, тому або:

1; 2; 3; 4;... - арифметична  прогресія, де , тому .

V. Фізкультхвилинка (Слайд 8) 

VI. Розв'язування задач прикладного змісту

2.               Прогресії в біології. Багатьом здається, що математика, це така наука, яка не має жодного зв’язку з природою, тваринним світом.(Слайд 9)

Англійський соціолог  Т. Мальтус та творець теорії походження видів Чарльз Дарвін вважали, що всі організми в природі мають тенденцію розмножуватися в геометричній прогресії. При цьому кожний вид теоретично має безмежні можливості  збільшувати чисельність особин.

Розглянемо, наприклад, квітку маку. «Достигла маківка повна крихітних зернинок» - К. Ліней. Підрахували, що вона містить більше 3000 зернинок. Що звідси випливає? Те, що коли б навколо нашої макової рослини була б достатня площа відповідної землі, кожна зернинка, яка впала, проросла б, і наступного літа на цьому місці виросло б вже 3000 маків.

Кожна з 3000 рослин дасть не менше однієї маківки, яка містить по 3000 нових рослин і т.д.   

1 рік -3000;

2 рік 30003000=9 000 000;

3 рік 90000003000=27 000 000 000;

І т.д. (Демонструють плакати).

На п’ятому році макам стане тісно на земній кулі, оскільки число рослин дорівнюватиме  243 000 000 000 000 000.

Поверхня ж усієї суші, тобто материків та островів земної кулі, становить лише 135 мільйонів кв.км., приблизно  в 2000 разів менше, ніж виросло б рослин  маку.

Чому ж у дійсності ми не спостерігаємо такого надзвичайно швидкого розмноження?

- Тому що величезна  кількість насіння гине не проростаючи!

Це правильно не тільки для рослин, а й для тварин, комах.

Розглянемо для прикладу, як швидко розмножується усім відома кімнатна муха. Нехай кожна кімнатна муха відкладає 120 яєць і нехай протягом літа встигає з’явитися 7 поколінь мух, половина з яких – самиці. За літо при безперешкодному розмноженні могли б протягом одного літа народитися від однієї пари така величезна кількість, що, вишикувавши їх у пряму лінію, одна  біля одної, всі ці мухи простяглися б на відстань, яка у 18 разів більша, ніж відстань від Землі до Сонця ( тобто близько, як від Землі до далекої планети Уран).

Як відомо, у Австралії не існувало кролів, коли цей материк було відкрито європейцями. Кріль завезений туди наприкінці XVIII століття, і оскільки там немає хижаків, які живляться кролями (умови близькі до теоретичних), то розмноження пішло надзвичайно швидким темпом, що завдало страшенної  шкоди сільському господарству. На боротьбу з цим лихом було кинуто величезні кошти.

Інтенсивне розмноження бактерій в геометричній прогресії широко застосовується в харчовій промисловості, у фармакології, в медицині.

Задача 19.12. Бактерія, потрапляючи в сприятливе середовище, наприкінці двадцятої хвилини ділиться на дві бактерії, кожна з яких наприкінці наступних
20 хв ділиться знову на дві й т.д. Скільки бактерій утвориться з однієї бактерії протягом доби?

Розв’язання

Кількість бактерій зростає за геометричною прогресією:

1, 2, 4, 8, 16, ..., у якої - число  поділів бактерії протягом доби , т.т 24 год.

Отже, кількість бактерій, що утворюється з однієї бактерії  протягом доби дорівнює сумі 72 перших членів геометричної прогресії

 (бактерій).

Відповідь: бактерій.

3.               Прогресії у фізиці. Ми переконалися, що прогресії застосовуються не тільки в математиці. Прогресії виражають закони деяких фізичних явищ. Наприклад, за законом геометричної прогресії здійснюється поділ нейтронів при ядерній ланцюговій реакції.

     У фізиці є таке поняття як «рівноприскорений рух». Якщо кажуть, що тіло рухається рівноприскорено, то це означає, що відстань, яку воно проходить за кожну наступну одиницю часу збільшується на одну й ту саму величину. Тоді як при рівномірному русі тіло за кожну одиницю часу проходить однакову відстань. Рух також може бути і рівносповільненим. Відрізки шляху за рівноприскореного руху утворюють арифметичну прогресію.(Слайд 10)

Задача 17.34. Під час вільного падіння тіло за першу секунду проходить 4,9 м, а за кожну наступну – на 9,8 м більше , ніж за попередню, якщо не враховувати опір повітря. Знайдіть час падіння тіла з висоти 490 м (опором повітря знехтувати).

Розв’язання

 

Маємо арифметичну прогресію перший член якої дорівнює 4,9, різниця -  9,8, а сума n  перших членів дорівнює 490. Розв’язання задачі зводиться до визначення n.

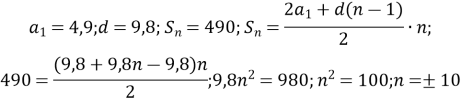
n= -10 – не задовольняє умову задачі;

n=10 с – час падіння тіла.

Відповідь: 10 с

4. Прогресії у  банківській справі (Слайд 11)

Існує думка, що разом з винаходом колеса створення банків стало одним з найважливіших винаходів людства.  Перший банк був заснований у Венеції 1171 року. З того часу банківська система розширюється і вдосконалюється.

     Комерційні банки виконують дві основні функції:

• зберігають грошові вклади;
• надають кредити (позики).

Якщо помістити до банку грошовий вклад, то банк виплачує вкладнику деяку суму грошей за те, що користується його капіталом для надання позик. Причому розмір вкладу зростає за законом геометричної прогресії.

Задача 18.17. Вкладник поклав до банку 5000 грн. під 8% річних. Скільки грошей буде на його рахунку через три роки?

Розв’язання

Нехай а₀ – початковий капітал вкладника, тобто a₀=5000 грн. Позначимо а₁, а₂, а₃ – кількість грошей на рахунку  відповідно в кінці першого, другого та третього року. Послідовність а₀, а₁, а₂, а₃ є геометричною прогресією , знаменник якої дорівнює 108%=1,08, n=4.

Тоді , а₃ =

Відповідь: 6298,56 грн.

В сучасних ринкових умовах ми   повинні бути компетентними у фінансових питаннях, і тому фінансова освіченість особистості, як ніколи, на першому місці.

Задача. Уявіть, що вам деяка фірма пропонує свої послуги. Щодня ви можете брати у фірми по 100 грн. Але за перший день ви зобов'язані заплатити фірмі 1к, за другий - 2к, за третій - 4к. і т. д. Чи укладете ви з цією фірмою договір не менш ніж на 20 днів за таких умов?

Розв'язання:

Від фірми отримуємо - 2000 грн,  а повинні будемо заплатити за це суму, що дорівнює 8го для геометричної прогресії, де . Тобто:

1048575(коп.)=10485грн. 75к

Вчитель робить зауваження, що в сучасних ринкових умовах учні повинні бути компетентними у фінансових питаннях, і тому освіченість особистості, як ніколи, на першому місці.

VIІ. Підсумок уроку. (Слайд 12) 

Учитель . Наш урок підходить до кінця, я думаю, що кожен із вас ще раз переконався у практичному застосуванні прогресій у різних сферах людської діяльності. І доцільними,  на мою думку, будуть ці віршовані рядки.

           Прогрес - це рух вперед , зростання,

          Як Україні зараз він потрібний.

          Прогресії - його сестриці рідні.

          Це школа, математика, навчання.

          І кожен з вас, нехай як  аксіому, знає:

          Без математики на ноги нам не стати.

          То ж хай лунає лозунг наш крилатий

          Прогресу без прогресій не буває!

Інтерактивна вправа «Інтерв’ю»

Я хочу, щоб кожен з вас пояснив, чому вважає за потрібне вміти розв’язувати задачі на застосування прогресій.

Учні висловлюють свої міркування .

Рефлексія.

 Обери (за бажанням) і допиши незакінчене речення.  (Слайд 13)

• Я дізнався …
• Я був здивований тим, що ….
• Я знайшов підтвердження тому, що …
• Мені сподобалось …..
• Я був розчарований тим, що …
• У мене з’явилось бажання …
• Урок мені дав для життя…

Оцінювання учнів

VIIІ. Домашнє завдання.

Повторити §3 п.  16 – 17(формули, правила), виконати Завдання № 4 «Перевірте себе» (№№ 11 - 16) с. 194. (Слайд 14)