Урок "Пропорція. Основна властивість пропорції"

Тема уроку. Пропорція. Основна властивість пропорції

Мета уроку:

Формування компетентностей:

предметна компетентність:  ввести поняття пропорції та її членів, навчити учнів читати пропорції, знаходити невідомий член пропорції, застосовуючи основну властивість пропорції; розвивати вміння працювати з підручником, опрацьовувати математичні тексти; розвивати культуру усних і письмових обчислень.

Спілкування державною мовою: грамотно висловлюватися рідною мовою, розуміти, пояснювати і перетворювати тексти математичних задач.

Математична компетентність:  виробити вміння пропорцію під час розв’язування типових завдань.

Уміння вчитися впродовж життя: контролювати та оцінювати результати своєї навчальної діяльності.

Тип уроку: вивчення нового матеріалу.

Хід уроку

1. Організаційний момент.

МАТЕМАТИКА

 Важка, цікава, легка, непотрібна, весела, незрозуміла, захоплююча, потрібна, нецікава, зрозуміла.

Якою для вас є математика? Оберіть потрібні слова.

Яке слово головне  в цьому переліку? (Потрібна)

2. Актуалізація знань.

Відома актриса Фаіна Раневська говорила: «Людина більше хвилюється про свою зовнішність, але не про свій мозок». Дійсно, людський мозок постійно потребує тренування. Але як же змусити свій мозок працювати? У цьому нам допоможе математика, її різноманітні й цікаві завдання. Тож будемо тренувати мозок?

Гра: «Мозковий штурм»

•       1. Яку назву ми можемо дати записам 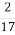  або 2 : 17?
•       2. Що називається відношенням двох чисел?
•       3. На що вказує відношення?
•       4. Як називаються члени відношення?
•       5. Як зміниться відношення, якщо його попередній і наступний члени збільшити у 12 раз?
•       6. У скільки разів 6 га більше за 2 га?
•       7. Яку частину метра складають  7см?
•       8. Яку частину метра складають 7 дм?
•       9. Чому дорівнює відношення чисел 40 до 10?
•       10. Чому дорівнює відношення чисел 10 до 40?
•       11. Відношення числа х до 8 дорівнює 2. Чому дорівнює х?
•       12. Відношення числа 27 до числа y дорівнює 9. Чому дорівнює y?

3. Мотивація навчальної діяльності

Тато купив 1,5 кг бананів за 39 грн, а  мама — 2 кг мандаринів за 52 грн. Що дорожче: банани чи мандарини?

39:1,5=52:2

Властивості таких рівностей і будемо вивчати.

4. Оголошення теми та мети уроку.

Сьогодні на уроці ми вивчимо:

•         Означення пропорції;
•         Елементи пропорції;
•         Основну  властивість пропорції.

А також навчимося

   застосовувати вивчені властивості для виконання вправ.

Слово «пропорція» походить від латинського «proportio», що означає співрозмірність, тобто має правильне співвідношення між частинами і цілими.

Першими відношення та пропорції вивчали давньогрецькі математики. 2500 років тому у Греції існувала математична школа, послідовники якої називали себе Піфагорійцями тому, що засновником цієї школи був Піфагор. Зараз  ми продовжимо вивчати відкриття піфагорійців. Серед них є вчення про пропорції, яке застосовується майже в усіх галузях людської діяльності.

5. Сприймання та усвідомлення нового матеріалу.

Чи є серед записаних відношень рівні?

Запишемо відповідні рівності.

Рівність двох відношень називають пропорцією.

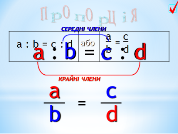Читаємо записані пропорції.

Визначаємо крайні і середні члени пропорції

Чи завжди потрібно знаходити значення кожного відношення, щоб перевірити чи правильна пропорція?

 Давайте спробуємо провести невелике дослідження.

Виберіть будь-яку пропорцію та заповніть таблицю:

Який висновок можна зробити?

В цьому й полягає основна властивість пропорції.

Добуток крайніх членів пропорції дорівнює добутку її середніх членів.

Чи з будь-яких чотирьох чисел можна утворити пропорцію?

Як це можна перевірити?

Утворіть (якщо можливо) правильні пропорції з чисел  1, 3, 5, 15

Висновок: Якщо поміняти місцями крайні або середні члени правильної пропорції, то одержимо правильні пропорції

Що робити, коли один із членів пропорції невідомий?

Щоб знайти невідомий крайній член пропорції, треба добуток середніх членів поділити на відомий крайній член.

Щоб знайти невідомий середній член пропорції, треба добуток крайніх членів поділити на відомий середній член.

Знайдіть невідомий член пропорції (по рядах)

Навіщо потрібні пропорції? Вони потрібні для розвʼязування багатьох прикладних задач. На наступних уроках ми дізнаємося, що пропорції потрібні і біологам, і кулінарам, і бухгалтерам, і служителям мистецтва, і звичайним, простим людям.

Задача. З 2 т макулатури можна одержати 1,5 т чистого паперу. Школярі зібрали 28 т макулатури. Скільки чистого паперу можна одержати з макулатури, зібраної школярами?

6. Первинне закріплення знань

№605, № 607

7. Підбиття підсумків уроку.

•      Як ви вважаєте, слово «пропорція» суто математичне, чи його можна використовувати в інших галузях? (відповіді учнів).
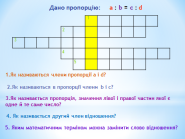
•      Пропорція має багато спільного з музикою, архітектурою, і навіть з природою.  А що саме, нам допоможе розібратися кросворд.
•      Дана пропорція:         a : b = c: d
•      1.Як називаються члени пропорції а і d. (крайні)
•      2.Як називаються в пропорції члени  b і c. (середні)
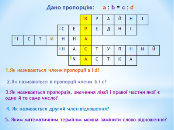•      3.Як називається пропорція, значення лівої і правої частин якої є одне й те саме число. (істинна)
•      4. Як називається другий член відношення. (наступний)
•      5. Яким математичним терміном можна замінити слово відношення. (частка)

Ми знайшли відповідь – краса. Отже природа і пропорція – це краса. Продовжіть моє речення: «Краса – це математика, краса – це музика, краса –це архітектура, краса – це закон природи, краса – це життя…

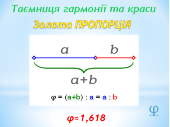
Чому ми захоплені, коли слухаємо музику, читаємо вірші, розглядаємо витвори архітектури, живопису, дивимося на павутинку, на розташування насіння соняшника? Бо все це створено за законами краси. Виявляється, що кришталик людського ока найкраще сприймає предмети, розміри яких перебувають у певному відношенні, яке називають золотим перерізом. Золотий переріз – гармонічна пропорція.

Число фі, є вкрай складним. У наш час воно розраховане із точністю до трильйона цифр після коми, тим не менше, це ще не кінець.

Відео.

7.Домашнє завдання.

п.20,

№ 606, 608 (дві задачі за вибором),

* перевірити, чи є ваша кімната «золотим» прямокутником