Урок "Пропорція. Основна властивість пропорції"

Тема уроку: Пропорція. Основна властивість пропорції

Мета:

 навчальна:  Ввести поняття пропорції, вивести основну властивість пропорції, формувати вміння й навички застосування її до розв'язування вправ; розглянути приклади використання пропорції у практичному житті

розвивальна: Розвивати в учнів творчі здібності, пізнавальний інтерес, інформаційні компетенції, логічно викладати думку, вміння застосовувати основну властивість пропорції для розв’язання рівнянь, формувати навички взаємоконтролю і самоконтролю.

виховна: Виховувати інтерес до предмету, працьовитість, наполегливість, охайність ведення записів, вміння об'єктивно оцінювати результати індивідуальної роботи.

Обладнання: підручник, зошит

Тип уроку: засвоєння нових знань.

Хід уроку

І. Організаційний момент:

Привітання, перевірка присутності учнів та підготовки класу до уроку.

Перевірка домашнього завдання (фронтальна,  відповісти на запитання, які виникли в учнів при його виконанні).

ІІ. Актуалізація опорних знань.

З поняттям відношення ми вже знайомі. А чи добре ви їх засвоїли, ми зараз дізнаємось.

Усне опитування

1. Що називають відношенням двох чисел? (Частку двох чисел або звичайний дріб називають ВІДНОШЕННЯМ цих чисел)

2. Яка основна властивість відношення? (відношення двох чисел не зміниться, якщо кожне із чисел відношення помножити або поділити на одне й те саме число, відмінне від нуля)

3. Що нам показує відношення? (Відношення показує, у скільки разів перше число більше за друге або яку частину перше число складає від другого)

4. Що означає запис: а > b  та  а < b ? (Якщо а > b, відношення показує, у скільки разів перше число більше за друге.

Якщо а < b, відношення показує,  яку частку перше число складає від другого).

5. Як знайти відношення двох величин, виміряних тією самою одиницею вимірювання? (потрібно знайти відношення їх числових значень, значення відношення однойменних величин є числом без найменування, наприклад: 5 км до 15 км дорівнює 5:15 = )

6. Як знайти відношення однорідних величин, виражених різними одиницями вимірювання? (потрібно спочатку перейти до однієї одиниці вимірювання , а потім знайти відношення їх числових значень)

7. Чи існує відношення різнойменних величин? ( Відношення різнойменних величин – це величина, значення якої залежить від вибору одиниць вимірювання величин, що є членами відношення.

Наприклад, швидкість – це відношення пройденої відстані до часу.

          5 км : 60 хв = 5 км : 1 год = 5 км/год                

8. Які відношення називають оберненими? (наприклад, відношення 7 до 2 і 2 до 7, називають  взаємно оберненими).

ІІІ. Сприйняття і усвідомлення нового матеріалу.

1. Формулювання проблеми у формі проблемного завдання.

Перед учнями ставиться завдання, виконання якого приведе до досягнення запланованих результатів.

З’ясуй, які з відношень рівні.

16 : 8;  15 : 5;  4,5 : 9;  1 : ;   2 : 1;   10 : 20.

2. Запишемо рівні відношення у вигляді рівності.

16 : 8 = 2 : 1;

4,5 : 9 = 10 : 20.

Одержані рівності називають пропорціями.

І ми почнемо вивчати одну із найцікавіших тем математики.

Запишемо в зошитах тему нашого уроку « Пропорція. Основна властивість пропорції»

3. Пояснення нового матеріалу

Розглянемо ще приклад

Відношення  12 : 3 та 20 : 5

12 : 3 = 4;

20 : 5 = 4

Іх частки однакові, тому можемо записати:

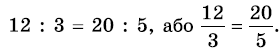
Рівність двох відношень називають пропорцією

Записують:    a : b = c : d             або             =

Читають: «Відношення а до b дорівнює відношенню с до d» або

«а так відноситься до b, як с відноситься до d».

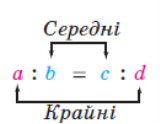
       Числа а і d називають крайніми членами пропорції,

         а числа b і с – середніми членами пропорції

Одну проблему ми з вами вирішили: дали означення пропорції.

     Яка наступна проблема?

Яку властивість мають пропорції?

Для вирішення цієї проблеми, пропоную вам

1) Знайти добуток крайніх членів пропорції;

2) Знайти добуток середніх членів пропорції.

10 : 4 = 50 : 20

Зробіть висновок: Добуток крайніх членів пропорції дорівнює добутку її середніх

членів:

Продовжимо наші дослідження

Чи порушиться пропорція, якщо ми поміняємо місцями крайні члени? Середні члени?

Дана пропорция 18 : 6 = 24 : 21,

1) Поміняйте місцями крайні члени пропорції. Чи буде нова пропорція вірною?

2) Поміняйте місцями середні члени пропорції. Чи буде нова пропорція вірною?

3) Поміняйте місцями крайні і середні члени пропорції. Чи буде нова пропорція

вірною?

В першому і другому випадку одержемо вірну пропорцію.

Висновок: середні члени або крайні члени пропорції можна міняти місцями

     Яка наступна проблема?

Знайти невідомий член пропорції.

1)      x : 28 = 3 : 12

2)        30 : y = 5 : 8.

Розв’язування

1) x : 28 = 3 : 12

 12 • x = 28 • 3

x =   = 7

2)  30 : y = 5 : 8

5 • y = 30 • 8

y =   = 48

Правила знаходження невідомого члена пропорції

1. Щоб знайти невідомий крайній член пропорції, треба добуток її середніх членів поділити на відомий крайній член пропорції.

2. Щоб знайти невідомий середній член пропорції, треба добуток її крайніх членів  поділити на відомий середній член пропорції.

Фізкультхвилинка

Встаньте, діти, посміхніться,

Землі нашій поклоніться

За щасливий день вчорашній.

І до сонця потягніться.

В різні боки нахиліться.

Веретеном покрутіться.

Раз присядьте, два присядьте.

ІІІ. Закріплення і осмислення нового матеріалу.

Вивчення пропорції має велике значення для практики. Пропорція застосовуються при виконанні різних розрахунків, що мають своїм завданням розподіл величин. 

Наприклад, за допомогою пропорції можна вирішити чимало

практичних задач у різних  галузях – медицині, кулінарії, будівництві, дизайні, сільському  господарстві тощо. А щоб краще дізнатися, як і де застосувати пропорції,  розглянемо з вами невеличкі відомості про практичне застосування пропорції у нашому житті. Та розв’яжемо декілька задач

Категорія «Кулінарія»

У кулінарії без пропорції не обійтися. Для приготування страв потрібно робити розрахунки. Наприклад, без обчислень не обійтись під час консервування плодів, приготування смачного варення, випіканні тортів, тістечок, складання меню для поживного харчування з наявних продуктів. Іноді в процесі готування деяких страв дозволяється один продукт заміняти іншим. Але одразу постає питання: яку ж кількість нового продукту треба взяти? Дати відповідь допомагають пропорції.

Задача 1.

У кулінарії допускається заміна 50г риби на 45г рибних консервів у томаті. Скільки потрібно консервів для заміни 7,5кг риби?

Розв’язування

Риба        консерва

50г      –        45г

7,5кг     –      х кг

50 : 7,5 = 45 : х

Х = 6,75

Відповідь: 6,75 кг

Категорія «Медицина»

В медичній практиці лікарі стежать за тим, скільки і коли потрібно давати ліків хворому. В правильних дозах ліки дають ефект, у менших – це некорисно, а в більших – приносить шкоду. При виготовленні ліків також дотримуються пропорції.

Задача 2.

У 100 грамах чорної смородини міститься приблизно 0,25 грама вітаміну С. Скільки грамів чорної смородини потрібно з’їсти людині за день, якщо одна добова доза вітаміну С складає 0,05 грама?

Розв’язування

Нехай х г чорної смородини потрібно з’їсти людині за день.

Запишемо коротко умову задачі у такому вигляді:

  Вітамін С           Смородина       

      0,25 г        –    100 г  

               0,05 г        –   х г      

0,25 : 0,05 = 100 : х

0,25 • х = 0,05 • 100

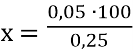= 20

Відповідь: 20 г чорної смородини потрібно з’їсти за 1 день

Категорія «Сільське господарство»

У господарствах, що спеціалізуються на вирощуванні великої рогатої худоби, доводиться складати раціони харчування тварин. Буває трапляється так, що один корм уже закінчився і треба замінити його іншим. Як це зробити, щоб не порушити раціону харчування? Для розв’яжемо задачу.

Задача 3.

При відгодівлі великої рогатої худоби 33 кг вівса дозволяється замінити 1,5 кг карбаміду (сечовина). Скільки потрібно карбаміду, щоб замінити 1210 кг вівса?

Нехай х кг – карбаміду потрібно взяти, щоб замінити 1210 кг вівса.

Розв’язування

Запишемо коротко умову задачі у такому вигляді:

  Карбамід           Овес       

             1,5 кг    –     33 кг

                х кг      –    1210 кг

Запишемо пропорцію  

1,5 : х = 33 : 1210

Х = 55(кг)

Відповідь: 55 кг  карбаміду міститься в 1210 кг вівса.

 Також не обійтися без пропорції в сільському господарстві при посівах полів. Потрібно знати і вміти як визначити кількість насіння, міндобрив, пального, щоб засіяти певну кількість гектарів поля.

Задача 4.

З 1,6 га землі, що становить 8% площі всього поля, зібрали 48 ц пшениці.

Скільки пшениці зібрали з усього поля, якщо врожайність на всьому полі однакова?

Розв’язування

8%       -  48 ц

100%     -  х ц

Запишемо пропорцію  

8 : 100 = 48 : х

Х = 600(ц)

Відповідь: 600 ц.

Категорія «Швейне виробництво»

 На швейному виробництві також потрібна пропорція. Потрібно вміти правильно визначати кількість тканими, щоб пошити плаття чи костюм.

Щоб краще зрозуміти, як це зробити, розв’яжемо задачу.

Задача 5.

На пошиття 14 однакових костюмів витратили 49 м тканини.

Скільки таких костюмів можна пошити з 84 м цієї тканини?

Розв’язування

Нехай х костюмів можна пошити з 84 м тканини.

Запишемо коротко умову задачі у такому вигляді:

Тканина  Костюми

49 м   –  14 шт

84 м   –   х шт

Записуємо пропорцію:

49 : 84 = 14 : х

Х = 24

Відповідь: 24 костюми пошили з 84 м тканини

Категорія «Фінанси»

 Без пропорції неможливо обійтися у фінансовій сфері. Потрібно вміти правильно розрахувати свої заощадження, щоб вони приносили вам прибуток. Ось для прикладу вам така задача.

Задача 6.

Клієнт банку поклав на депозит 3000 грн. Через рік він отримав прибуток у сумі 450 грн. Під  який  відсоток  поклав  гроші  клієнт до банку?

Розв’язування         

Поклав   -  3000 грн  - 100%
Отримав -  450 грн  -  х % 

3 000 : 450 = 100 : х

Х = 15

Відповідь: 15%

Задача 1. Вкладник поклав до банку 1000 грн, а через рік одержав

1180 грн. скільки відсотків річних сплачує банк?

 Задача 2. У кулінарії допускається заміна 50 г риби на 45 г рибних консервів у томаті. Скільки потрібно консервів для заміни 7,5 кг риби.

 Задача 3. З 0,3 т свіжих яблук виходить 57 кг сушених. Скільки можна одержати сушених яблук з 2,1 т свіжих?

 Задача 4. Для виготовлення 6 однакових приладів потрібно 14 кг металу. Скільки металу потрібно для виготовлення 15 таких самих приладів?

ІV. Підбиття підсумків уроку та оцінювання.

1. Що таке пропорція?
2. У пропорції m : n = p : k  назви крайні члени, середні члени
3. Сформулюй основну властивість пропорції
4. Які перестановки членів пропорції можна виконувати?

V. Повідомлення домашнього завдання: за підручником О.С. Істер.

  Математика: Підручник для 6 класу закладів загальної освіти

(у 2-х частинах) – К.: Ґенеза, 2023.

Опрацювати § 16, ст. 130 – 133.

Виконати: № 587, 589, 591.

VІ. Рефлексія

                Чи сподобався вам урок?

             Що не сподобилась на уроці?

             Що нового дізнався?

             Що найбільше запам’яталось?

На полях зошита намалюйте смайлик, який відповідає вашому настрою на кінець уроку.