Урок "Прямокутна система координат на площині. Відстань між двома точками із заданими координатами"

ДЕКАРТОВІ КООРДИНАТИ НА ПЛОЩИНІ.

УРОК ГЕОМЕТРІЇ В 9 КЛАСІ

 

Тема уроку. Прямокутна система координат на площині. Відстань між двома точками із заданими координатами.

Мета уроку:

дидактична: допомогти повторити, узагальнити та систематизувати набуті в попередніх класах знання учнів, ознайомитись учням із знаходженням відстані між двома точками із заданими координатами;

розвивальна: стимулювати розвиток уявлень учнів про методи геометрії та сферу застосувань сучасних інформаційних технологій;

виховна: сприяти вихованню в учнів акуратності геометричних побудов як елемента математичної культури.

Обладнання уроку: конспект, таблиця «Декартові координати та вектори на площині», комп’ютери, пакет динамічної геометрії DG, тестове середовище Є.А. Шестопалова TestW2, роздаткові матеріали «Очікувані результати», «Математичний диктант», «Чи правильно, що…», «Домашнє завдання», «Бонус»

Тип уроку: урок засвоєння знань, умінь і навичок.

Очікувані результати:

• учень описує прямокутну систему координат;
• учень записує і доводить формулу відстані між двома точками;
• учень застосовує вивчену формулу до розв’язування задач.

 

ХІД УРОКУ.

 

І. Організаційний момент (1 хв)

• Вітання, знайомство;
• Що потрібно на уроці(лінійка, олівець, гума, червона ручка)

 

ІІ. Актуалізація опорних знань (математичний диктант, max=3 бали, 3 хв)

1. Скільки осей зазвичай зображають на координатній площині? (2)
2. Вісь ОХ називають віссю … (абсцис)
3. Друга координата точки називається … (ординатою точки)
4. Початок координат – це точка з координатами … (0;0)
5. У якій чверті лежить точка з координатами (5;-100)? (IV)
6. Точка з координатами (5;0) віддалена від початку координат на відстань … (5)

Взаємоперевірка (ключ написано на дошці, 3 хв)

Розгляд апеляцій

 

ІІІ. Мотивація навчальної діяльності(1 хв)

Як знайти відстань від точки, що не лежить ні на одній з осей, до початку координат? Між двома точками із заданими координатами?

 

IV. Повідомлення теми і мети уроку(1 хв)

 

V. Очікувані результати учнів (на розданих бланках кожен учень записує, що він очікує від уроку, який бал він прагне і реально може отримати; 2 хв)

 

VI. План вивчення нового матеріалу

1. Розповідь про Рене (Картезія) Декарта (2 хв)

Народився в Лае (Турень) у 1596 році. Навчався в єзуїтській колегії в Ла-Флеш (провінція Анжу), потім вивчав медицину та право. Закінчив університет в Пуатьє у 1616 році. У 1618 році познайомився з Й. Бекманом, під впливом якого зацікавився математикою та фізикою. У 1637 році написав математичний трактат «Геометрія», в якому були закладені основи аналітичної геометрії. Він стверджував, що єдиним загальним методом математики є алгебраїчний. У своїх працях від він ввів метод ортогональних координат, узагальнив поняття про координатну площину. Найвідоміший його вислів – «Я мислю – отже, я існую!»

2. Прямокутна система координат. (2 хв)

Нехай задано деяку площину, наприклад, площина дошки. Проведемо у ній дві взаємно перпендикулярні прямі-осі. Точку перетину осей називають початком координат. Вона має координати (0;0). Така система координат називається прямокутною або декартовою.

Кожній точці на координатній площині можна поставити у відповідність єдину впорядковану пару чисел, і навпаки. Ця пара чисел називається координатами точки у даний системі координат.

Осі розбивають координатну площину на чотири необмежені області, які прийнято називати чвертями.

Повернемось до поставленої проблеми: яким чином можна визначити відстань від точки до початку координат?

 

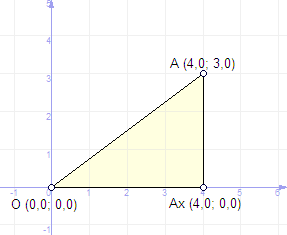Задача 1. (колективно у групах, 3+3 хв)

 

Дано: А(4;3)

Знайти: ОА.

 

Розв’язання.

Опустимо з точки А перпендикуляр на вісь абсцис. Розглянемо прямокутний Δ АА_хО. У ньому катет АА_х=3, ОА_х=4. Це випливає зі значень координат точки А. Згідно теореми Піфагора . Отже, ОА=5.

 

3. Теорема про відстань між двома точками із заданими координатами. (бесіда, 3 хв)

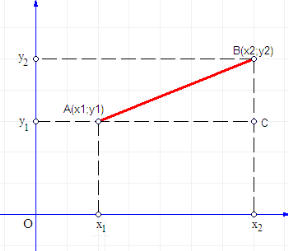
Розглянемо, як це буде в загальному випадку. Нехай задано дві точки на координатній площині своїми координатами: А(х₁;у₁) і В(х₂;у₂). Для спрощення, нехай обидві точки лежать у І чверті, при чому х₁< х₂, y₁< y₂. Опустимо з кожної точки перпендикуляри на обидві осі. Розглянемо катети прямокутного Δ АСВ. Маємо, що АС= х₂- х₁, а ВС= у₂- у₁. Довжина гіпотенузи трикутника є шуканою відстанню, тому зручно використати теорему Піфагора, згідно якої , а отже, .

Ми довели теорему про відстань між двома точками із заданими координатами:

Відстань між двома точками дорівнює кореню квадратному із суми квадратів різниць їх відповідних координат.

Ми розглянули випадок, коли обидві точки лежать в І чверті, але суть доведення не змінюється, якщо точки А і В лежать в ІІ, ІІІ, IV або в різних чвертях. Спробуйте довести теорему для інших випадків вдома самостійно.

Приклад використання доведеної теореми.

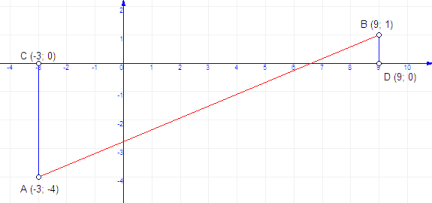
Задача 2.

 (колективно у групах, 3+3хв)

 

Нехай на малюнку зображено карту села Маркуші. Синім кольо-ром позначено дороги. Одиничному відрізку відповідає 10 м. У точці А розміщено будинок Васі, у точці В – магазин. На скільки коротший шлях від будинку Васі до магазину через городи (вздовж червоної лінії) за шлях по дорозі (вздовж ламаної ACDB)?

Розв’язання.

Обчислимо відстань АВ:

,

.

Обрахуємо довжину ламаної ACDB:

, .

Отже, йдучи через городи, а не дорогою, Вася пройде на (17-13)∙10=40 метрів менший шлях.

 

VII. Закріплення вивченого матеріалу. Формування вмінь і навичок.

1. Робота з роздатковим матеріалом «Чи правильно, що…» (1 хв)
2. Фізкультхвилинка. (1 хв)
3. Інструктаж з використання пакету динамічної геометрії (вікно середовища, інструменти Точка, Відрізок, Виміряти відстань та дії з ними; 1 хв).
4. Самоперевірка відповідей на матеріал «Чи правильно, що…» за допомогою використання пакету динамічної геометрії DG. Аналіз завдань (max=1 бали; 2 хв)
5. Тестування за допомогою тестового середовища TestW2. (max=5 бали; 4 хв)

 

VIII. Підведення підсумків уроку

Кожен учень підраховує свої бали, порівнює з очікуваними. (1 хв)

Рефлексія «Мікрофон» (4 хв)

 

ІХ. Домашнє завдання (1 хв)

Середній рівень: Знайдіть периметр Δ АВС, якщо А(-1;2), В(2;6), С(5;2).

Достатній рівень: Знайдіть площу Δ АВС, якщо А(1;0), В(2;), С(3;0). Доведіть, що даний трикутник – рівносторонній.

Високий рівень: Із заданих координатами восьми точок утворити зірку і обчислити її периметр.