Урок "Узагальнення теми «ПОДІБНІСТЬ ТРИКУТНИКІВ»"
Предмет : математика ( урок геометрії), інформатика.
Передбачається робота в таких середовищах: Microsoft Office PowerPoint ( презентація), easyQuzzy (тест), PowerPoint (робота з малюнком до задачі).
- 1.png png
- 2.png png
- 3.png png
- Інтегрований урок.pptx pptx
- Показати всі файли


Інтегрований урок з геометрії в 8 класі.
- формувати вміння і навички застосовувати ознаки подібності трикутників до розв’язування задач, вміння пояснювати поняття властивостей, методів, подій елементів керування в режимі виконання програми;
- удосконалювати навички розв’язування практичних задач;
- розвивати вміння узагальнювати, виховувати культуру усного математичного мовлення та пізнавального інтересу учнів;
- розвивати пізнавальну творчу діяльність та креативність учнів, вміння аналізувати й долати складні моменти;
- сприяти виникненню в учнів інтересу до вивчення геометрії, усвідомлення її краси та значущості;
- Виховувати інформаційну культуру, дбайливе ставлення до комп'ютерної техніки.
- виховувати дисциплінованість, повагу один до одного, свідомі мотиви навчання, позитивне відношення до знань.
Обладнання: комп’ютери, ноутбук, проектор, екран, картки для оцінювання, презентація до уроку, презентації для учнів, малюнки до задач, тест.
Тип уроку: інтегрований, комбінований
Вчителі: Н.С. Лукичова, М.М. Комов
Предмет (математика ( урок геометрії), інформатика)
Клас - 8
Тема - «Подібність трикутників»
Тип уроку - урок корекції і узагальнення знань, інтегрований.
Час - 45 хвилин
Обладнання уроку: комп’тер, проектор, екран, презентація, комп’ютерний тест, картки для оцінювання .
Медіапродукт
- Середа - Microsoft Office PowerPoint
- Вид медіапродукта - презентація
- Структура презентації:
|
№ п/п |
Структурні елементи |
Час |
№ слайда |
|
1 |
Організаційний момент |
5 хвилини |
Слайди 1-6 |
|
2 |
Актуалізація опорних знань: Проходження тесту за комп’ютером |
5 хвилин 7 хвилин |
Слайд 7 |
|
3 |
Актуалізація міжпредметних зв’язків:
|
7хвилин
|
Слайди 8-9 |
|
4 |
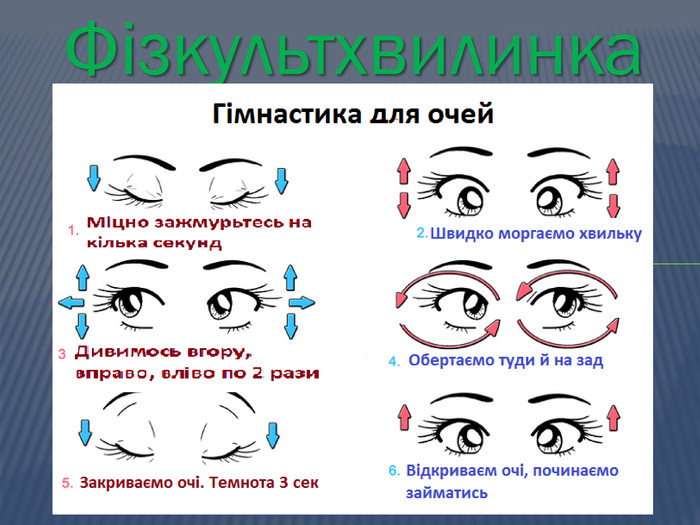
Фізкультхвилинка «Зорова гімнастика» |
1 хвилина |
Слайд 11 |
|
5 |
Корекція знань по темі «Застосівання подібності трикутників». Робота з малюнками у середовищі Paint |
12 хвилин |
Слайди 14-16 |
|
6 |
Підведення підсумків |
4 хвилини |
Слайди 17-18 |
|
7 |
Домашнє завдання |
3 хвилини |
Слайд 19 |
|
8 |
Джерела |
|
Слайд 20 |
- Організаційний момент (Слайди 1-6). (5 хв.)
Вчитель звертає увагу учнів на вислів відомого французського вченого , математика і фізика, Блеза Паскаля: «Об ’єкт математики настільки серйозний, що слід не пропускати нагоди зробити його трохи цікавішим». Та вислів архітектора Ле Корбюзьє «…Все навколо геометрія…»
- Актуалізація опорних знань (5 хв.)
Проходження тесту на комп’ютері.
«В минуле на машині часу» (Слайди 8-9 ) (5 хв.)
Коротке повідомлення про Фалеса ( учень біля дошки).
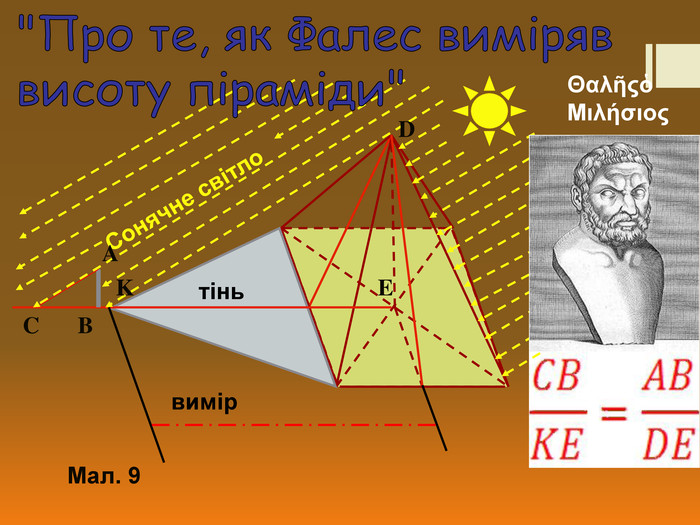
Використання подібних фігур зустрічається в Вавілоні та Єгипті раніше,ніж було визначено подібність. Ідея подібності розвивалась в різних країнах паралельно і виникла з потреби розв’язувати задачі на визначення розмірів недоступних предметів і відстаній до них. Відомо, що в кінці VII- поч. VI ст. до н. е. в м. Мілет, що в Греції, жив відомий астроном і математик Фалес Мілеський. Він вперше довів теореми про рівність кутів при основі рівнобедреного трикутника, рівність вертикальних кутів, про пропорційні відрізки . Фалес першим почав гру «Доведи», яка тягнеться і досі, і в яку грають всі математики. Він знайшов спосіб
*•
визначення відстані від берега до корабля , визначив висоту Єгипетської піраміди за довжиною її тіні , використавши подібність трикутників. Фалес міркував так. Сонце від Землі дуже далеко, тому проміні від нього можна вважати паралельними. Поряд з пірамідою він встановив вертикально жердину. Фалес стверджував , що довжина тіні піраміди відноситься до довжини тіні стовпа, як висота піраміди до висоти стовпа.
Учитель. (Слайд 10 ) Обчислити висоту піраміди, якщо:
висота жердини - 4 ліктя; довжина тіні жердини - 5 ліктів; довжина тіні піраміди - 200 ліктів.
Розв’язок: СВ:КЕ=АВ:ДЕ; 5:200=4:Х; Х=160 ліктів.
Фізкультхвилинка: Вправа для очей. (Слайд 11)
«Замороки з горщечка» (Слайд 12 ) (6хв.)
Капітани команд тягнуть номери задач з горщечка .
Задача 1. За способом Жуля Берна (мал. 10, слайд )
Звукове супроводження слайда №11 - шум моря.
З уроків зарубіжної літератури ви знайомі з відомим французьким письменником Жулем Верном. Він написав чудові романи. Один з них - «Таємничий острів».
Один учень читає уривок з роману.(дод.1)
![]()
![]()
![]()
![]()
(Від. = ; х = = 333 (футам)).
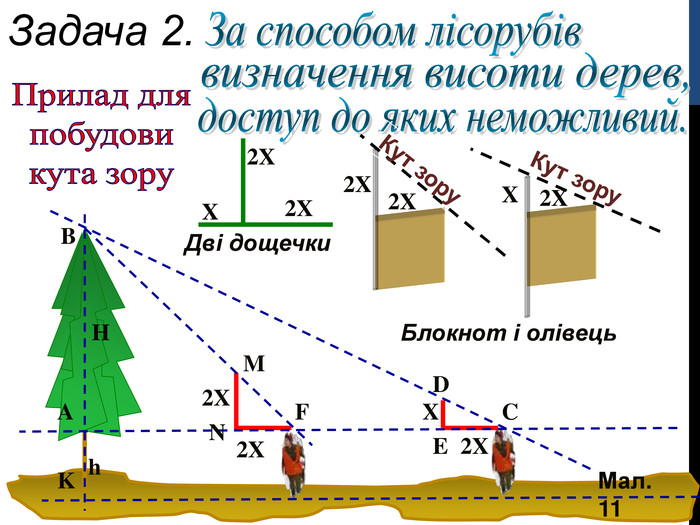
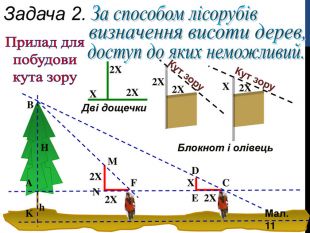
Задача 2. (мал. 11, слайд 13) За способом лісорубів визначення висоти дерев, доступ до яких недоступний.
Звукове супроводження слайда №12 - співи птахів.
Іноді неможливо виміряти великий об’єкт, або він недоступний. Існує спосіб, який використовують лісоруби для визначення висоти дерев. Вони використовують прилад для побудови кута зору (як видно з малюнка). Людина два рази, відповідно до малюнка, напрямляє кут зору для сполучення кінця приладу із верхівкою дерева.
(Від. З подібності BFA і MFN => AF=H; ВСА ~ DCE => АС = 2Н
=
FC = 2Н - Н = Н => ВС = FC + h, де h - ріст людини).
- Корекція знань по темі. (10 хв)
«Подібність трикутників у нашому житті» (слайди 14-16)
Робота з малюнками
Необхідні виміри: Відстань від спостерігача до жердини 5м, що удвічі менше за відстань від жердини до дерева. Висота жердини 1 м. 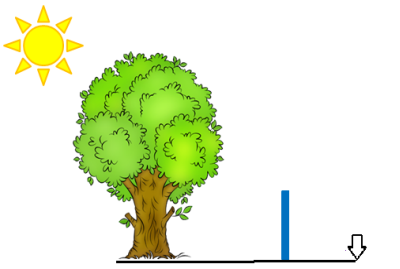
Творче завдання: у 7 класі на уроках фізики ви вивчали закони відбивання світла та використовували їх для побудови зображення в дзеркалі. Спробуйте застосувати свої знання з фізики та геометрії для розв’язання такої задачі: як можна визначити висоту сосни за допомогою дзеркала?
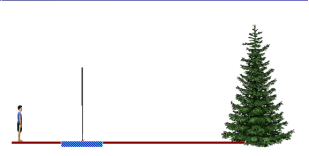
Необхідні виміри: Відстань від спостерігача до дзеркала 5м, що утричі менше за відстань до ялинки. Зріст спостерігача 1,5 м.
- Підведення підсумків (4 хв.) (Слайди 17-18 )
Створення власної прикладної задачі.
Підраховуємо бали, вибіраємо кращих гравців, виставляємо оцінки.
- Домашнє завдання слайд (Слайди 19 )


про публікацію авторської розробки
Додати розробку