Урок "Рівнобедрений трикутник та його властивості"

Відділ освіти Бердянської міської ради Запорізької області

 

 

 

 

 

 

 

 

ПРЕЗЕНТАЦІЙНИЙ УРОК З ТЕМИ

«Рівнобедрений трикутник, його властивості»

 

 

Урок підготувала

 учитель математики вищої категорії,

старший учитель

Бердянської гімназії №3 «Сузіря»

Пітюкіна О.Ю.

 

 

 

 

 

 

Бердянськ

 2021

 

 

Мета уроку:

        закріпити означення рівнобедреного трикутника, з'ясувати і довести властивості і ознаки рівнобедреного трикутника;

• повторити основні поняття з теми «Трикутник», визначення рівнобедреного і рівностороннього трикутника; довести властивості рівнобедреного трикутника; формувати вміння застосовувати ці властивості;
• виховувати інтерес до математики, історії математики. Показати безпосередній зв'язок математичних понять з оточуючим світом.

Завдання

• Активізувати раніше вивчені теоретичні знання про трикутники; перша і друга ознаки рівності трикутників.
• Систематизувати практичні навички додавання та віднімання дробів з однаковими знаменниками при розвязуванні рівнянь та прикладних задач.
• розвивати логічне і просторове мислення, творчу і розумову діяльність учнів, здатність до «бачення» проблеми; формувати здібності до оцінки власної діяльності,
• Виховувати стійкий інтерес  до шкільних  предметів,  розкриваючи зв`язок між ними.
• Розвиток комунікативних навичок учнів.
• Розвивати аналітичне мислення.
• Розвивати вміння працювати в колективі.
• Виховувати загальну культуру та культуру спілкування.
• Розвивати навички пошукової діяльності.
• Розширювати ерудицію учнів.

 

 

 

Очікувані результати:

знаннєвий компонент - учні добре володіють термінологією, демонструють застосування основних означень і правил на прикладах розвязання  задач, вміння працювати з різними видами тестів;

діяльнісний компонент - учні демонструють навички роботи в парах та в групах, вміння ставити запитання та відповідати на них,  початкові вміння презентувати свої проекти и робити перші висновки;

ціннісний компонент  - учні усвідомлюють необхідність вивчення даної теми.

Тип уроку: вивчення нового матеріалу з елементами інтеграції …

Обладнання: проектор, ноутбук, презентація.

 

Хід уроку.

І. Організаційний момент. (слайд 1)

     Вчитель

     Вітаю! Сідайте! Сьогодні в нас з вами нестандартний урок – відкрите судове засідання, на якому присутні прокурори, адвокати, свідки і журналісти. Через декілька років вам обирати професію, і, можливо, хтось з вас звʼяже своє життя з професією юриста, або життя поставить вас у таку ситуацію, коли треба буде звернутися до суду, тому сьогодні ми отримаємо знання не тільки з математики, а й станемо більш соціально розвинутими. На столі у кожного з присутніх є лист засідання, який вам треба заповнити  в ході засідання. Ознайомтеся.

II. Мотивація навчальної діяльності. (слайд 2-6)

     Вчитель. (секретар судового засідання).

     Суддя – Скорик Софія. 

     До суду з позивною заявою звернувся  журналіст видання «Твоє місто» Тонєва Анастасія Романівна

«Можна перерахувати дуже багато професій, пов'язані з трикутником, але мене цікавить архітектура мого міста – «Чи є  трикутники  ефективними інструментами для архітектури і можливо їх використання при проектуванні будівель та інших споруд, оскільки перш за все треба забезпечити міцність і стійкість споруди?»

III. Актуалізація опорних знань. (слайд 7)

       Вчитель. Для того щоб всі присутні зрозуміли про який трикутник йде мова, пригадаємо деякі  факти, які будуть використані в лінії захисту:

• Що таке трикутник?
• Як називають  трикутники залежно від довжин їхніх сторін?
• Які сторони рівнобедреного трикутника називають бічними сторонами? Яку сторону називають основою?
• Що таке медіана трикутника; бісектриса; висота?
• Скільки можна провести в трикутнику медіан, бісектрис і висот?
• Які трикутники називаються рівними?
• Назвіть першу ознаку рівності трикутників
• Означення суміжних кутів та їх властивість

IV Вивчення нового матеріалу (слайд 8)

        Вчитель. Розглядається справа – обвинувачення рівнобедреного трикутника у відсутності властивостей і як результат неможливості використання в спорудах.

        Суддя  - Слово надається прокурору Вероніці Юріївні:

        Ваша Честь, я хочу надати документ з практичними викладками, який свідчить по те, що в рівнобедреному трикутнику всі кути різні. Отже, його непрактично використовувати в архітектурі.

В                            37°              71°                      72°          А                        С

      

 

        Суддя  - У адвокатів є запитання?

        Адвокат  - Да, Ваша Честь.

       

       Вчитель – Слово надається адвокату Любові Павлівні (слайд 9)

        Ваша честь, я можу довести, що не всі, але, принаймні, кути при основі – рівні.

 

Доведення властивості біля дошки:

                    B                               Дано ∆ABC, AB=BC

                                                      Довести ∟А=∟С, ВК – медіана, висота

 

 

      A            K          C

  Доведення.

• Проведемо  бісектрису ВК до основи АС 
• Розглянемо два отриманих трикутника ∆АВК і ∆СВК. У них АВ=ВС, ВК – спільна, ∟АВК=∟СВК – за означенням бісектриси. Отже,  ∆АВК = =∆СВК за першою ознакою.
•   Звідси, ∟А=∟С

Отже, в рівнобедреному трикутнику кути при основі рівні.

А вимірювання кутів транспортиром, який має похибки, не є доведенням. Дякую, Ваша Честь.

 

Суддя – У обвинувачення є інші аргументи?

 

Прокурор – Так, Ваша Честь.

 

Вчитель – Слово надається Данилу Олеговичу

     Ваша Честь, я хочу надати інший документ з практичними викладками, який свідчить про те що, якщо в ∆ABC провести бісектрису, медіану і висоту з кута А, то це три різні відрізка.

В                                                 АМ - медіана                                                 АК - бісектриса                                  М            АН - висота                                    К                                      Н      А                                        С

 

     Суддя – У захисників є питання?

     Адвокат – Так, Ваша Честь.

      Вчитель – Слово надається Марку Сергійовичу

     Я доведу, що в рівнобедреному трикутнику бісектриса, проведена до основи,  трикутника є медіаною і висотою. На основі доведення Любові Павлівни можна зробити щє висновки (на тому ж самому малюнку):

З рівності ∆АВК і ∆СВК стверджуємо, що відповідні сторони і кути рівні, отже, АК=СК, а значить що, ВК – медіана; ∟АКВ=∟СКВ=180°:2=90° - ВК – висота. Отже, ми робимо висновки – властивості рівнобедреного трикутника: (слайд 10)

 «В рівнобедреному трикутнику кути при основі рівні»

 «В рівнобедреному трикутнику бісектриса, проведена до основи   трикутника, є медіаною і висотою» . Дякую, Ваша Честь.

         Суддя – Оголошується перерва на 2 хв.

V Фізкультхвилинка: (слайд 11)

     Вчитель – слово надається журналісту - Ярошенко Аріні

     Видання «Як зберегти здоров’я?» Хочу привернути увагу всіх присутніх до двох видів рівнобедрених трикутників –гострокутний        і

                                                                          тупокутний

і порахувати кількість трикутників кожного виду, розташованих в залі засідання (3 і 12). Як ви вважаєте: «З чим пов’язані отримані числа?»  Дякую за увагу.

         Суддя – Продовжується засідання

VI Закріплення нового матеріалу (слайд 12)

•         Вчитель – Захист викликає свідка – Бен Алайю Сарру

       Рівнобедрені трикутники використовувались в архітектурі східної будівлі Національної картинної галереї у Вашингтоні, столиці США. Будівля Флатірон у Нью-Йорку є одним з найбільш інноваційних хмарочосів у світі. Ця будівля побудована на трикутному блоці на Манхеттені, надаючи їй трикутну форму, зокрема, рівнобедрену. Він стоїть вже більше 100 років, демонструючи силу трикутної архітектури

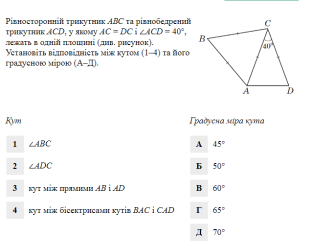
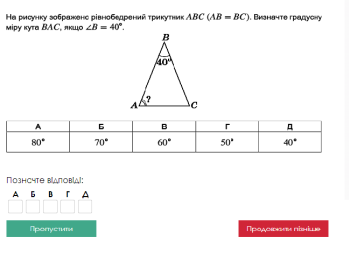•        Вчитель – Пропоную вислухати думки всіх бажаючих з питання: «Як можна використовувати властивості рівнобедреного трикутника для розрахунків елементів архітектурних споруд (розв’язування тестових завдань за текстами ЗНО) (слайд 13,14)  

   

•        Вчитель – Ми вислухали обидві сторони – обвинувачення та захисту, для прийняття рішення суддею нам потрібно виконати останній крок – пройти кожному On-line тестування на платформі «На урок»  за посиланням, розташованим в групі Viber  https://naurok.com.ua/test/join?gamecode=8307525 

(слайд 15)

 

VI Рефлексія

    Вчитель. Суддя оголошує вирок.

     Суддя. Розглянувши у відкритому судовому засіданні справу про рівнобедрений трикутник і його властивості суд встановив, що  рівнобедрений трикутник має властивості - «В рівнобедреному трикутнику кути при основі рівні», «В рівнобедреному трикутнику бісектриса, проведена до основи   трикутника, є медіаною і висотою». Ухвалив використання властивостей рівнобедреного трикутника у розв’язанні задач. Без геометричних понять і алгебраїчних розрахунків неможлива реалізація архітектурного об'єкта.

   VII Домашнє завдання (слайд 15)

Домашнє завдання розташоване на моєму блозі (де ви знайдете цікаву презентацію про трикутники). Вам треба зайти за посиланням, https://pityukina.blogspot.com/p/blog-page_8.html , розташованому в вайбері в нашій групі і виконати домашнє завдання.

 

VII. Підсумок  уроку. (слайд 16)

Вчитель. А тепер я хочу надати слово кожному, хто бажає поділитися своїми враженнями від уроку «вільний мікрофон»:

• Про що ми дізналися?
• Що зрозуміли?
• Що допомогло у розумінні теми?
• У чому ми переконалися?
• Де ви зможете задіяти отримані знання?

Молодці! Дякую всім за активну роботу на уроці.

                               Лист засідання від 03.12.2021р

«Рівнобедрений трикутник та його властивості»

План засідання

1. Доведення властивостей

         B                                    Дано ∆ABC, AB=BC

                                                          Довести ∟А=∟С, ВК – медіана, висота

 

 

      A           K             C

Доведення.

_______________________________________________

          _______________________________________________

          _______________________________________________

          _______________________________________________

          _______________________________________________

Отже, властивості доведені.

«В рівнобедреному трикутнику кути при основі рівні»

 «В рівнобедреному трикутнику бісектриса проведена до основи   трикутника є медіаною і висотою»

2. Розв’язування задач (за тестами ЗНО)

 

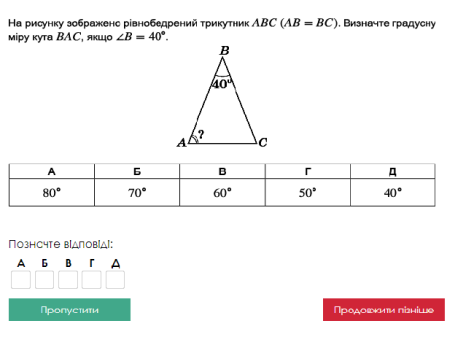
Кількість балів за On-line тестування  _________

Домашнє завдання

Домашнє завдання розташоване на моєму блозі (де ви знайдете цікаву презентацію про трикутники). Вам треба зайти за посиланням, https://pityukina.blogspot.com/p/blog-page_8.html , розташованому в вайбері в нашій групі і виконати домашнє завдання