Урок " Робота з полярною системою координат"

Робота з полярною системою координат

Для побудов графічних примітивів, які складаються з ліній і прямокутників легко можна використовувати Декартову перевернуту систему координат, яку використовує графічний режим Pascal. Проте, для роботи з окружностями вона є дещо незручною, оскільки є прямолінійною. У випадку розрахунків чи побудови графіків складних функцій, або знаходження точок на колі чи дузі зручніше використовувати полярну систему координат.

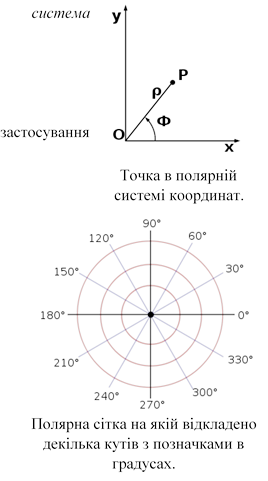
Полярна система координат — двовимірна координат, в якій кожна точка на площині визначається двома числами — кутом та відстанню. Полярна система координат особливо корисна у випадках, коли відношення між точками найпростіше зобразити у вигляді відстаней та кутів; в більш поширеній, Декартовій, або прямокутній системі координат, такі відношення можна встановити лише шляхом тригонометричних рівнянь.

Полярна система координат задається променем, який називають нульовим або полярною віссю. Точка, з якої виходить цей промінь називається початком координат або полюсом. Будь-яка інша точка на площині визначається двома полярними координатами: радіальною    та         кутовою.         Радіальна

координата (зазвичай позначається r) відповідає відстані           від точки до початку координат. Кутова координата, що також зветься полярним кутом або азимутом і позначається φ, дорівнює куту, на який потрібно повернути проти годинникової стрілки полярну вісь для того, щоб потрапити в цю точку.

Визначена таким чином радіальна координата може приймати значення від нуля до нескінченості, а кутова координата змінюється в межах від 0° до 360°. Однак, для зручності область значень полярної координати можна розширити за межі повного кута, а також дозволити їй приймати від'ємні значення, що відповідатиме повороту полярної осі за годинниковою стрілкою.

Проте, для того, щоб зобразити фігуру в графічному режимі Pascal, необхідно, все ж, координати представляти не в полярній, а в Декартовій системі. Для цього існують наступні співвідношення: Зв'язок між декартовими та полярними координатами x=r*cos (ϕ); y=r*sin (ϕ);

Оскільки в даних співвідношеннях присутні тригонометричні функції, то необхідно провести ще деякі корективи – значення кутів у цих функціях завжди подається не в градусній, а і радіанній мірі:

x=r*cos (ϕ/180*π); y=r*sin (ϕ/180*π);

Також, оскільки в нашому випадку вісь 0Y перевернута, то остаточні перетворення матимуть вигляд:

x=r*cos (ϕ/180*π);

y=-r*sin (ϕ/180*π);

Задача: Написати програму, що малює знак радіації, який зображено на рисунку.

Дану фігуру найзручніше будувати за допомогою дуг та ліній, оскільки при використанні інших фігур такого ефекту з даними кольорами досягти неможливо. Для початку визначимося з розмірами і кутами сегментів фігури. Для цього виконаємо наступну побудову:

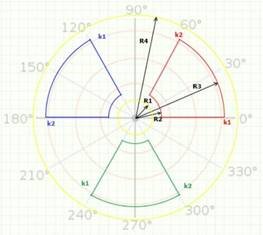
Задамо наступні значення: R1=40, R2=60, R3=200, R4=230.

Код програми: Program Prapor;  uses graph, crt;

 var gr, gd, x, y,r1,r2,r3,r4,k1,k2:integer;  begin   gd:=detect;

initgraph(gr,gd,'../bgi');

if graphresult<>0 then writeln('ERROR')    else     begin     x:=getmaxx div 2;     y:=getmaxy div 2;

r1:=40; r2:=60; r3:=200; r4:=230;

setcolor(14);     circle(x,y,r1);

 k1:=0; k2:=60;     arc(x,y,k1,k2,r2);     arc(x,y,k1,k2,r3); line(trunc(x+r2*cos(k1/180*pi)),trunc(y-r2*sin(k1/180*pi)), trunc(x+r3*cos(k1/180*pi)),trunc(y-r3*sin(k1/180*pi))); line(trunc(x+r2*cos(k2/180*pi)),trunc(y-r2*sin(k2/180*pi)), trunc(x+r3*cos(k2/180*pi)),trunc(y-r3*sin(k2/180*pi)));     k1:=120; k2:=180;     arc(x,y,k1,k2,r2);     arc(x,y,k1,k2,r3); line(trunc(x+r2*cos(k1/180*pi)),trunc(y-r2*sin(k1/180*pi)), trunc(x+r3*cos(k1/180*pi)),trunc(y-r3*sin(k1/180*pi))); line(trunc(x+r2*cos(k2/180*pi)),trunc(y-r2*sin(k2/180*pi)), trunc(x+r3*cos(k2/180*pi)),trunc(y-r3*sin(k2/180*pi)));

k1:=240; k2:=300;     arc(x,y,k1,k2,r2);     arc(x,y,k1,k2,r3); line(trunc(x+r2*cos(k1/180*pi)),trunc(y-r2*sin(k1/180*pi)), trunc(x+r3*cos(k1/180*pi)),trunc(y-r3*sin(k1/180*pi))); line(trunc(x+r2*cos(k2/180*pi)),trunc(y-r2*sin(k2/180*pi)), trunc(x+r3*cos(k2/180*pi)),trunc(y-r3*sin(k2/180*pi)));

circle(x,y,r4);     setfillstyle(1,14);     floodfill(x,y-r1+1,14); floodfill(x,y-r4-1,14);     end;   readkey;   closegraph; end.