Урок "Розв’язування геометричних прикладних задач на обчислення об’ємів тіл"

Тема уроку: Розв’язування прикладних задач на обчислення об’ємів тіл.

розвивальна: розвивати в учнів інтерес до вивчення геометрії; виховувати охайність при виконанні записів;

виховна: виховувати інтерес до предмета, любов до прекрасного.

Тип уроку: Урок закріплення вивченого матеріалу.

Обладнання: моделі геометричних фігур: пряма призма, піраміда, циліндр, конус, куля; рухомі моделі геометричних фігур; плакат “Фігури стереометрії”; плакати для ілюстрації задач зроблені в програмі Microsoft Office Word; кросворд зроблений в програмі Microsoft Office Publisher; фломастери; матеріали з Вікіпедії (електронна енциклопедія); публікації зроблені в програмі Microsoft Office Power Point; таблиця густин речовин.

ХІД УРОКУ

I. Організація класу.

•          інструктаж з техніки безпеки при роботі на комп’ютері;
•          повідомлення теми уроку;
•          мотивація навчальної діяльності учнів;
•          конкурс рефератів на тему “Стереометрія”: учні повідомляють джерело, одержаної ними інформації;
•          повідомлення історичних відомостей.

II. Повторення раніше вивченого матеріалу.

1. Повторення теоретичного матеріалу.

Використовується презентація №1 зроблена в програмі Microsoft Office Power Point.

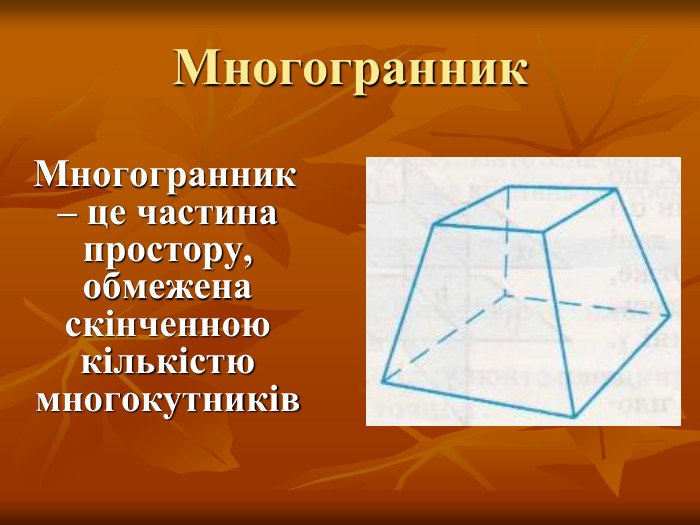
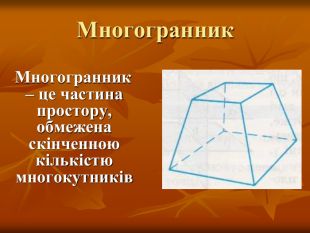
• що називається многогранником;
• що таке призма;
• яка призма називається прямою;
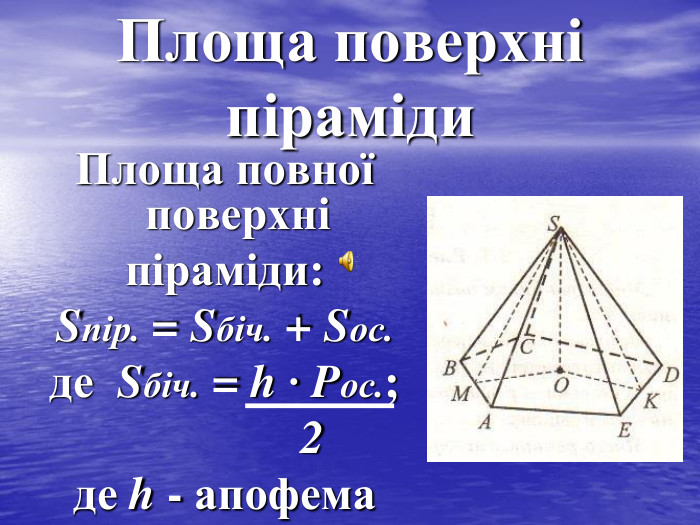
• яка фігура називається пірамідою;
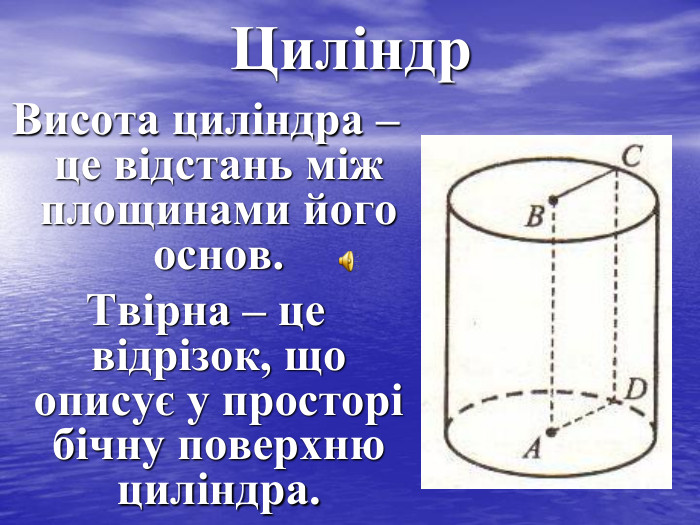
• дати означення циліндра;
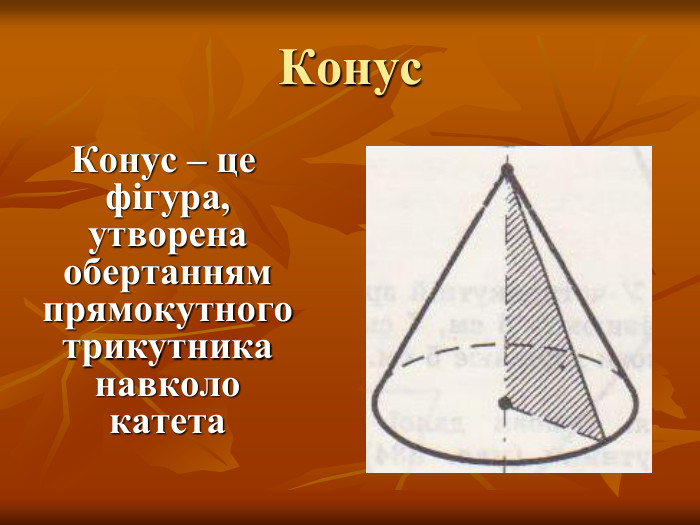
• що називається конусом;
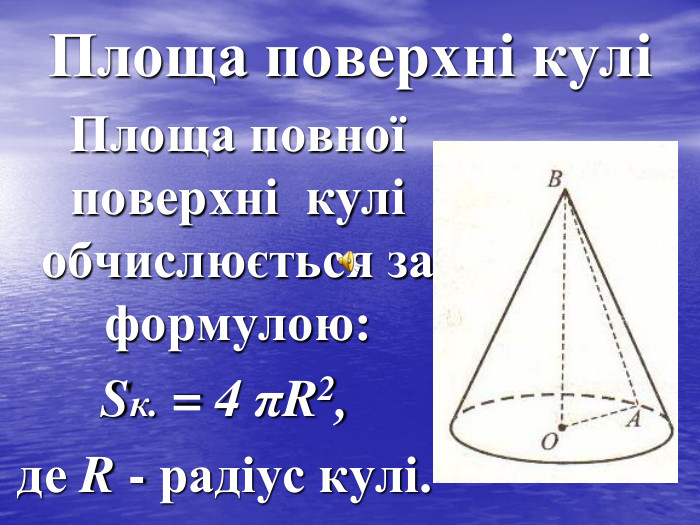
• що таке куля;
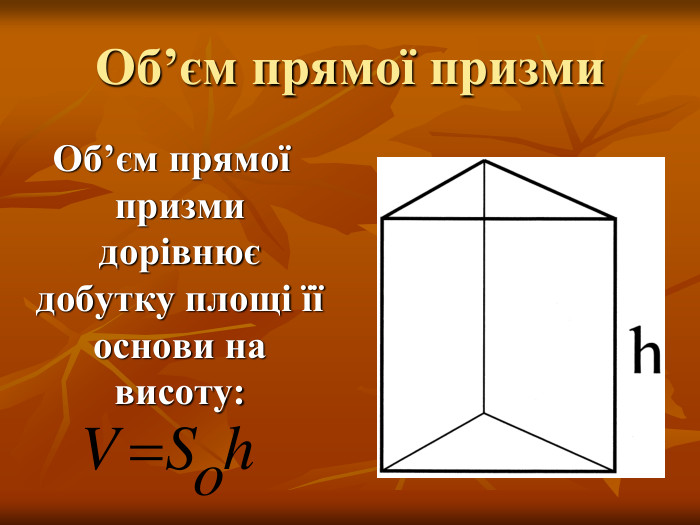
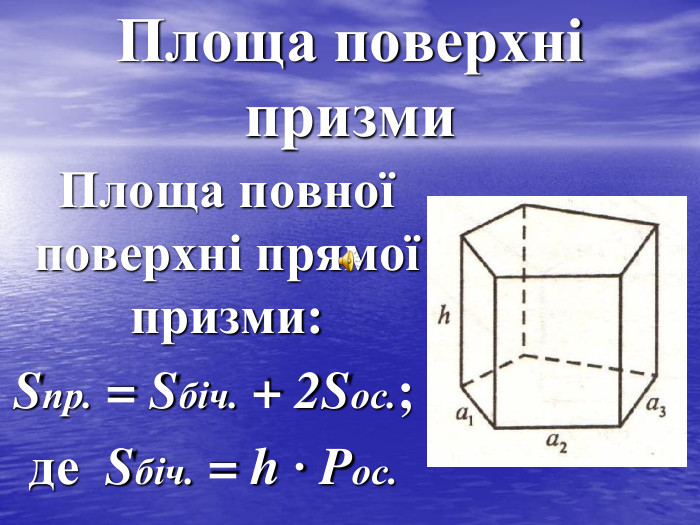
• як знайти об’єм прямої призми;
• як обчислити об’єм піраміди;
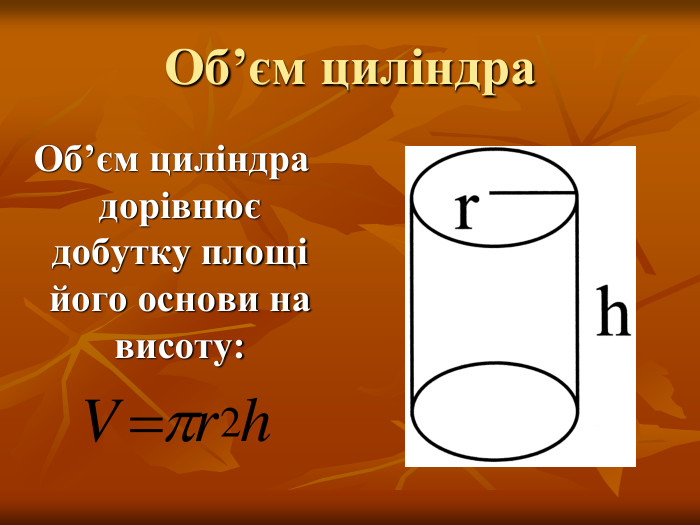
• як знайти об’єм циліндра;
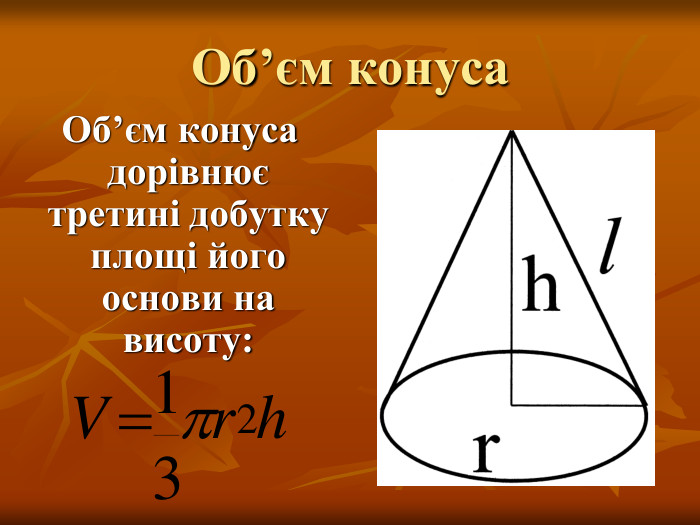
• як обчислити об’єм конуса;
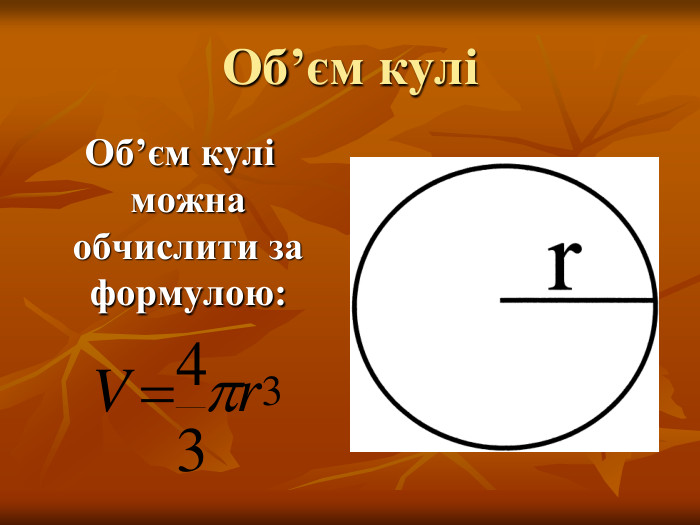
• як знайти об’єм кулі.

  2. Змагання між двома командами.

Потрібно вказати вірність формулювання за допомогою сигнальних кольорів на комп’ютері (зелений колір – вірна відповідь; червоний колір – невірна відповідь).

Використовується презентація №2 зроблена в програмі Microsoft Office Power Point.

• основи циліндра рівні та паралельні;
• осьовим перерізом циліндра є круг;
• висота і твірна циліндра – це один і той же відрізок;
• осьовий переріз конуса – це правильний трикутник;
• твірні  конуса різні по довжині;
• вісь  конуса і  його висота рівні;
• осьовий переріз зрізаного конуса – це паралелограм;
• поверхня  кулі – це сфера;
• переріз кулі площиною – це коло;
• твірні циліндра не паралельні осі циліндра;
• твірні конуса паралельні осі конуса;
• куля – це результат обертання півкруга.

III. Розв’язування прикладних задач на обчислення об’ємів тіл.

Для розв’язування пропонуються слідуючі задачі.

Задача 1

Знайти масу “Золотого м’яча”, який отримав відомий футболіст Андрій Шевченко, якби цей м’яч був повністю із золота. Дані, яких не вистачає, знайти самостійно.

Задача 2

Знайти скільки поміститься шампанського в Кубок Чемпіонів, який в свій час виграв Андрій Шевченко, якщо його внутрішня частина – це конус з діаметром   42   см  і   висотою  42 см.

Задача 3

Яка товщина нафтової плівки на воді, якщо вона покриває круг діаметром 30 см і утворена внаслідок розтікання 1 г нафти ?

Дані, яких не вистачає, знайти самостійно.

Задача 4

На цукровому заводі резервуар для мийки буряка виготовлено у вигляді прямої призми, в основі якої лежить трикутник із сторонами 5 м, 5 м, 6 м, а висота його 10 м. Резервуар спочатку    заповнюють    водою     на

60 %. Скільки води міститься у резервуарі ?

Підказка: площу основи знайти по формулі Герона.

Задача 5

Продаються два кавуни одного сорту: один обхватом 60 см, а другий – 50 см. Перший в 1,5 рази дорожчий. Який кавун краще купити.

Підказка: Знайти відношення об’ємів кавунів.

Задача 6

Для перевезення нафти використовуються цистерни, що складаються з циліндра і двох півкуль. Довжина циліндричної частини 10 м, а її радіус 2 м. Скільки потрібно таких цистерн для перевезення 500 м³ нафти ?

IV. Розгадування кросворду.

Учням     пропонується    для   розгадування  слідуючий   кросворд;   мета – визначення ключового слова.

V. Підсумок уроку

   Використовується презентація №3 зроблена в програмі Microsoft Office Power Point.

VI. Оцінювання учнів.

VII. Домашнє завдання.

       Дати диференційоване індивідуальне домашнє завдання.