Урок "Розв'язування логарифмічних рівнянь"

Конспект урок

Математика

11 клас

Тема: Розв’язування логарифмічних рівнянь.

Мета:

Навчальна: засвоїти означення логарифмічного рівняння; навчити розв’язувати логарифмічні рівняння різними методами (розв’язування найпростіших логарифмічних рівнянь; використання рівнянь-наслідків; Рівняння з однаковими основами; рівняння, які зводяться до простіших за допомогою перетворень; заміна змінних у логарифмічних рівняннях та графічний спосіб);

Розвиваюча: розвивати вміння розв’язувати логарифмічні рівняння різними способами;

Виховна: виховувати впевненість у власних силах, необхідність розкривати науковий потенціал.

Тип урок: засвоєння нових знань.

Обладнання: підручник, карточки із завданнями, презентація.

Девіз уроку: «За допомогою рівнянь, теорем. Я безліч всяких вирішив проблем». (Чосер, англійський поет)

 

 

Хід урок

Ⅰ. Організаційний етап.

Слово вчителя: «Добрий день, діти, шановні колеги. Я рада всіх вас  вітати на нашому уроці.»

Перевірити готовність учнів до уроку та налаштувати їх на роботу.

 

ІІ. Перевірка домашнього завдання.

Перевірити наявність та якість виконання домашнього завдання та відповісти на запитання учнів, які виникли під час виконання.

 

ІІІ. Актуалізація опорних знань.

Ось і пролунав дзвоник на урок математики, на урок нових відкриттів та роздумів.

 «Серед усіх наук, які відкривають шлях до пізнання законів природи, найважливішою є математика»

Це слова відомої жінки-математика Софії Ковалевської і ми спробуємо це довести.

Отже наші предки, піднявшись на дві ноги, невтомно передавали  свої знання дітям, для того, щоб вони дійшли до нас. І частину цих знань, названою наукою алгеброю, ми спробуємо відтворити, узагальнити, систематизувати сьогодні на уроці.

 

Ⅳ. Мотивація навчальної діяльності. Повідомлення теми та мети уроку.

Знання з математики допомагають людині жити в сучасному світі, пізнавати всі його дива і таємниці. Саме математика -  знаряддя, за допомогою якого людина пізнає і підкоряє собі навколишній світ.

При розв’язуванні завдань біля дошки учні використовували основну логарифмічну тотожність та властивості логарифмічної функції. Сьогодні на уроці ми розглянемо поняття  найпростіших логарифмічних рівнянь та метод їх розв’язування.

 

V. Сприймання і усвідомлення нового матеріалу.

При введенні поняття логарифму і властивостей логарифмічної функції необхідно звернути увагу на вміння застосовування основної логарифмічної тотожності, а також на формулу переходу від однієї основи логарифма до іншої. Приступаючи до розв’язування логарифмічних рівнянь, треба враховувати, що всі властивості логарифмічної функції були доведені за умови, що вирази, які стоять під знаком логарифма, додатні.

Логарифмічними рівняннями називають рівняння, які містять змінну під знаком логарифма.

Приклади логарифмічних рівнянь: .

Рівняння виду , називають найпростішим логарифмічним рівнянням. Це рівняння можна розв’язати, використовуючи означення логарифма. З означення логарифма випливає, що має єдиний корінь.

Існує декілька видів логарифмічних рівнянь і різних способів їх розв’язання. Основними з них є:

1. За означенням логарифма.

2. Метод введення нової змінної.

3. За властивостями логарифмів та логарифмічної функції.

4. Функціонально-графічний метод.

При розв’язуванні логарифмічних рівнянь, треба знайти ОДЗ рівняння або виконати перевірку, бо деякі перетворення можуть привести до одержання сторонніх коренів.

В основному, всі логарифмічні рівняння, які ми будемо розв'я­зувати, зводяться до розв'язування найпростіших рівнянь.

 

Задача 1. Розв’яжіть рівняння

Розв’язання. За означенням можна записати: .

 Звідси  ; :

Відповідь:

Задача 2.

Розв’язання. Знаходимо ОДЗ:

.

Тоді за означенням логарифма можна записати:.

Звідси ; .

Значення задовольняє ОДЗ.

Відповідь: 4.

Під час розв’язання багатьох логарифмічних рівнянь застосовують таку теорему.

Теорема: Якщо  , то рівняння виду

рівносильне будь-якій із систем

;   

Задача 3. Розв’яжіть рівняння

Розв’язання. Дане рівняння рівносильне системі ,

Маємо: 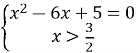,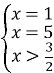. Звідси x=5.

Відповідь:5.

Задача 4. Розв’яжіть рівняння

Розв’язання: Оскільки , то дане рівняння рівносильне рівнянню . Нехай . Тоді отримаємо

Звідси , отже . Тоді початкове рівняння рівносильне сукупності , .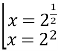

Відповідь:

 

VІ. Набуття умінь розв’язувати найпростіші логарифмічні рівняння.

Усно:

1. Якому з наведених проміжків належить корінь рівняння  ?

А) (5;8]; Б)(8;11]; В)(-1;2); Г) (2;5); Д)(-4;-1).

2. Скільки коренів має рівняння на відрізку [-5;5]?

А) жодного; Б) один; В) два; Г) три.

Виконати письмово:

1. Розв'яжіть рівняння:

А) ;

Розв’язання. За означенням можна записати: .

 Звідси  ; :

Відповідь:

 

Б) ;

Розв’язання. За означенням можна записати: .

 Звідси  ; :

Відповідь:

В) .

Розв’язання. За означенням можна записати: .

 Звідси  ; :

Відповідь:

2. Розв’яжіть рівняння:

1. ;

Розв’язання. Дане рівняння рівносильне системі ,

Маємо: ,. Звідси x=2.

Відповідь:2.

2. .

Розв’язання. Дане рівняння рівносильне системі ,

Маємо: ,. Звідси x=1.

Відповідь:1.

3. Розв’яжіть рівняння:

1. ;

Розв’язання.

,

,,

,

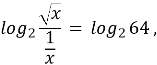
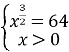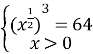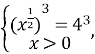
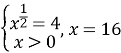
Маємо: ,. Звідси x=2.

Відповідь:2.

2.

Розв’язання. Перейдемо до логарифма із основою 2.

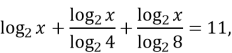
Відповідь: 64.

4. Розв’яжіть рівняння:

1. ;

Розв’язання.

При вираз не визначений, це число не є коренем рівняння.

Відповідь:4.

2.

Розв’язання.

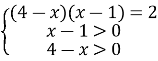
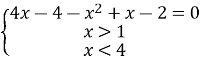
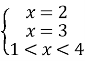
Відповідь. 2,3.

 

Ⅶ. Підсумки уроку.

•              Чого навчилися під час уроку?
•              З якими труднощами ви зустрілися?
•              Що допомогло подолати труднощі?

 

Ⅷ. Домашнє завдання.

•                 Опрацювати §6, с.32-34;
•                 Повторити властивості логарифмів;
•                 розв’язати № 6.2, № 6.4,  №6.6, №6.8.