Урок "Розв’язування показникових нерівностей"

Конспект уроку №7

Тема: «Розв’язування показникових нерівностей»  Мета :

-                      навчальна: формувати в учнів уміння розв’язувати показникові нерівності, закріпити знання про властивості графіків показникової функції, формувати вміння та навички застосовувати отримані знання для розв’язування задач прикладного характеру;

-                      розвивальна: розвивати логічне мислення, пізнавальну активність; 

-                      виховна: виховувати графічну культуру, увагу, культуру математичної мови.

Тип уроку: формування умінь та навичок.

Обладнання: Таблиця «Показникова функція».

Хід уроку І. Організаційний момент.

ІІ. Перевірка домашнього завдання.

ІІІ. Актуалізація опорних знань.

Поки клас усно перевіряє домашнє завдання, три учні біля

дошки розв’язують завдання:

№466 (б,г)

б) (√6)^х ≤ 1/36 (61/2)х ≤ (1/6)2 х/2 ≤ 6^-2 х  ≤ -4 Оскільки 6˃1, то у=6^t є зростаючою, тобто більшому значенню аргумента відповідає більше значення функції.

змінюються.

Графічно розв’язати нерівність 3^х  ≥ 4-х.

В одній і тій самій системі координат будуємо графіки функцій у=3^х та у=4-х.

Складемо таблицю:

  По графіку бачимо, що 3^х ≥ 4-х, якщо х≥1

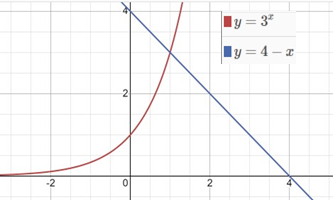Відповідь: [1;+ _∞].

Враховуючи     відповіді   на запитання учнів, які виникли при виконанні         домашнього завдання.

Усно. Розв’язують нерівності з таблиці:

I ряд – I стовпчик; II ряд – II стовпчик; III ряд – III стовпчик

IV Формування умінь розв’язувати показникові нерівності 1) З класом:

a) розв’язати нерівність 5^х2+2х ≥ 5³  

Функція у=5^t зростає, тому дана нерівність рівносильна нерівності  х²+2х≥3

                                                      х²+2х-3≥0

Розв’яжемо цю нерівність методом інтервалів:

х²+2х-3 ≥ 0 х₁ = -3 х₂ =1

б)4^х - 12∙2^х +32≥0 2^2х - 12∙2^х +32≥0 Введемо нову змінну 2^х=t t ² - 12t + 32≥0 t² - 12^t + 32=0

                  t₁=4        t₂=8

(t-4) (t-8) ≥0

Розв’яжемо цю нерівність методом інтервалів

Повернемось до минулої змінної:

                   2^х≤4;            2^х≤2²; х≤2,

                   2^х≥8;            2^х≥2³; х≥3

Відповідь: х є (-∞;2]  [3; +∞)

2) Розв’язати нерівність:

a)    2х2-1<8

2х2-1<23 

Функція у=2^t зростає, тому що дана нерівність рівносильна нерівності х²-1<3 х²-1-3<0 х²-4<0

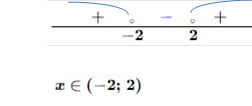
b)   32х-х2 < 9

32х-х2 < 32 

Функція у=3^t зростає, тому дана нерівність рівносильна нерівності:

2х-х² < 2 -х²+2х-2<0 х²-2х+2˃0

(х-1)²+1 ˃0 при будь-яких х.

c)    3^2х2-6 ˃1/81

32х2-6 ˃3-4 

Функція у=3^t зростає, тому дана нерівність рівносильна нерівності:

2^х2-6 ˃-4

2^х2-6+4˃0

2^х2-2˃0

2(х²-1)˃0

2(х-1)(х+1)˃0

Відповідь: хє (-∞;-1)  (1;+∞) 3) 4^х-2^х+1-8 ˃0

2^2х-2^х∙2-8 ˃0

Введемо нову змінну 2^х=t t²-2t-8 ˃0 t²-2t-8 =0 t₁=4  t₂=-2

(t-4)(t+4) ˃0

t ˃ 4, t< -2;   Повернемось до минулої змінної:

                           2^х ˃4,             2^х ˃2²,                х ˃2

                          2^х<-2;             2^х<-2;                 0

Відповідь: хє (2;+ ∞)

V       Підсумок уроку:

Отже, на уроці ми навчились розв’язувати показникові нерівності; з’ясовувати рівень засвоєння учнями знань і вмінь; розвивали логічне мислення; формували навички самостійної роботи; застосовувати теоретичні знання на практиці.

VI   Домашнє завдання:

1)   Розв’язати рівняння: а) √2^х∙√5^х=1000

                                                                       б)4^х-9∙2х+8=0

                                                                       в) 4-3^х-1+3^х+1=117

2)   Розв’язати нерівність: а) 1,5^х ˃2,25

                                                                 б)4^х+2^х≥6

3)   Розв’язати систему рівнянь:  2^х+2^у=6,

                                                                               х+у=3;