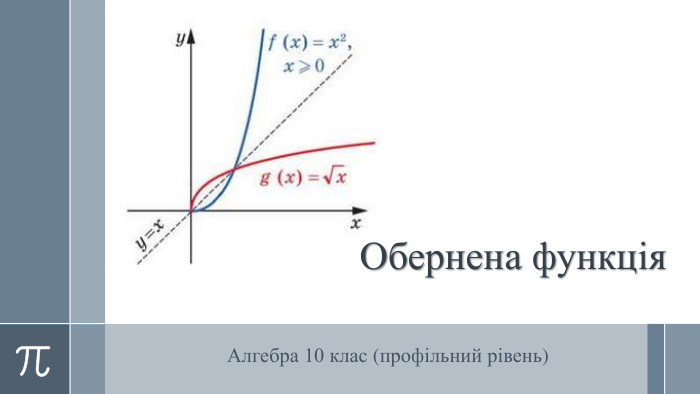
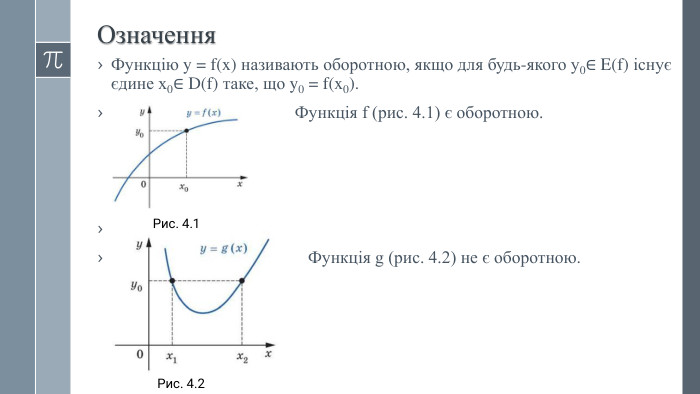
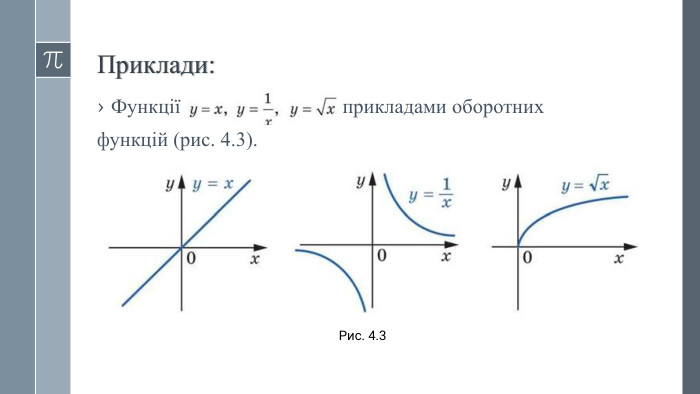
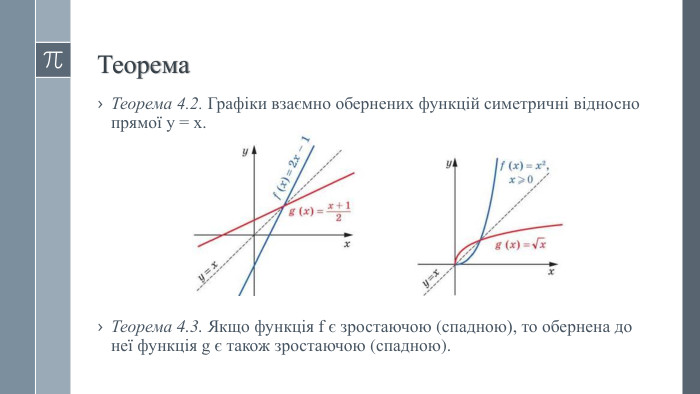
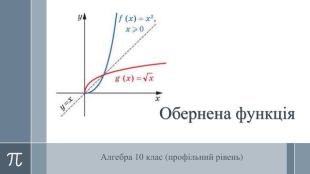
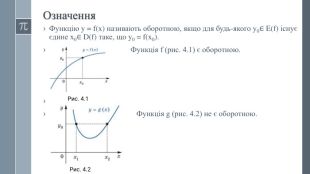
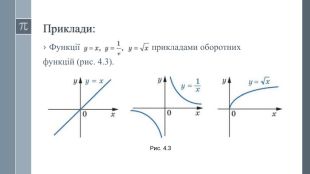
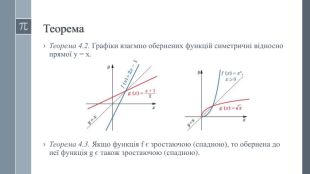
Урок "Обернена функція"
Про матеріал
Теоретичний матеріал та вправи до теми "Обернена функція" та його застосування. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку