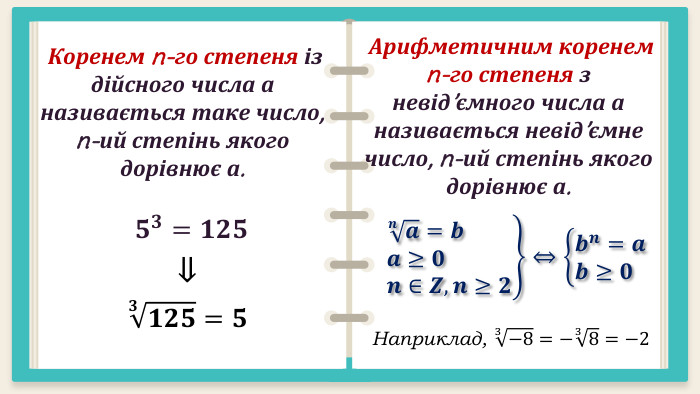
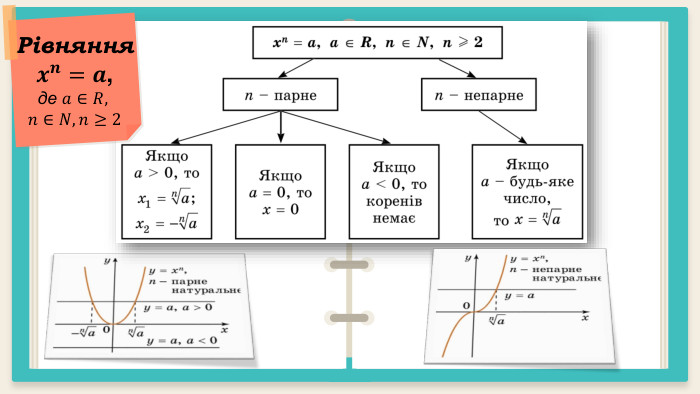
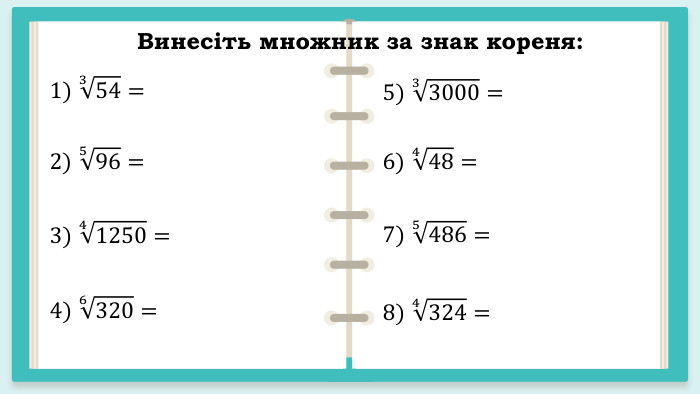
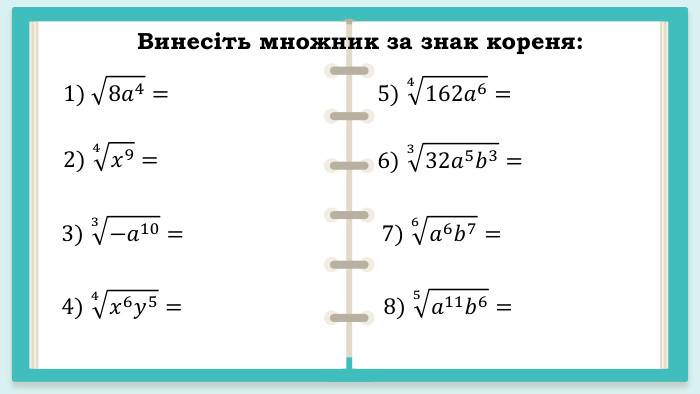
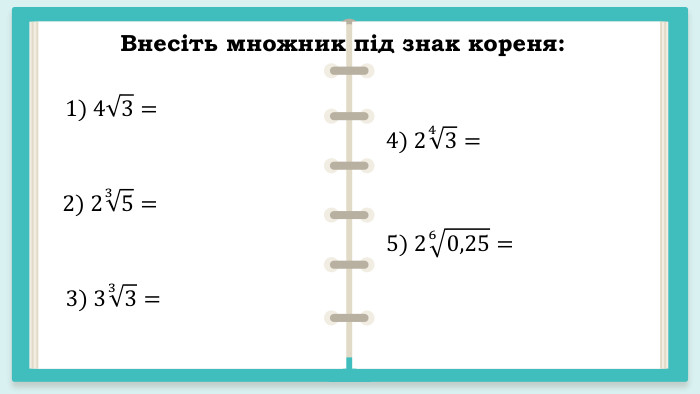
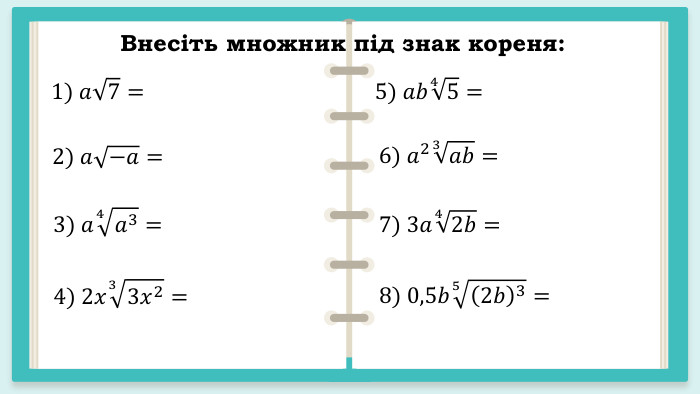
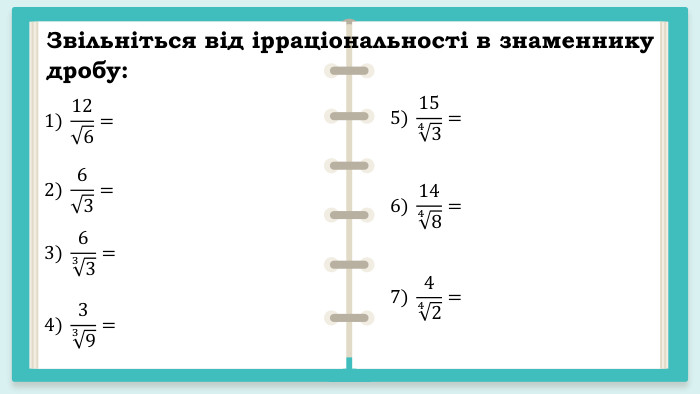
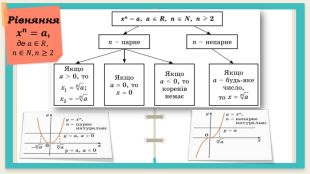
Презентація "Корінь n – го степеня. Арифметичний корінь n – го степеня та його властивості"
Про матеріал
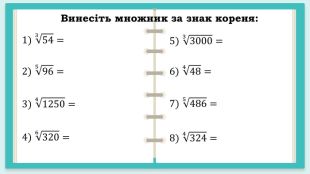
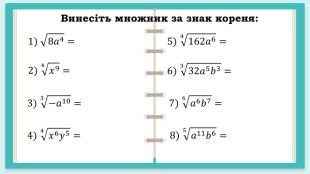
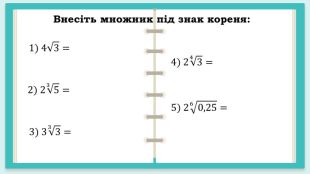
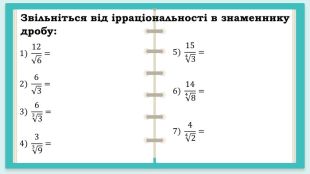
Завдання до уроку "Корінь n – го степеня. Арифметичний корінь n – го степеня та його властивості" Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку