Урок "Розв'язування прикладних задач"

Тема: Об’єми та площі поверхонь геометричних тіл. Розв’язування прикладних задач     

Мета уроку:

навчальна  - повторити теоретичний матеріал з теми «Об’єми та площі поверхонь геометричних тіл», узагальнити, систематизувати і поглибити знання учнів про об’єми геометричних тіл при розв’язуванні практичних задач;

розвивальна - розвивати вміння творчо мислити,  працювати самостійно, робити висновки;

виховна - виховувати самостійність, як засіб інтелектуального розвитку, працьовитість, кмітливість, інтерес до нових знань і прагнення їх набути;

Тип уроку: вдосконалення вмінь і навичок при розв’язку задач

Дидактичне та матеріально-технічне забезпечення:

моделі многогранників та тіл обертання, роздатковий матеріал, плакат.

 

Хід уроку:

І. Організаційна частина -  (  3 хв.)

•                                                                                                                                     Перевірка наявності учнів.
•                                                                                                                                     Перевірка готовності учнів до уроку.
•                                                                                                                                     Перевірка організації робочих місць.

ІІ. Мотивація навчальної діяльності

Антична мудрість стверджує «Знання – це сила». На мою думку, знання – це одна із сходинок до успіху в майбутньому. І сьогодні ми будемо плідно працювати, щоб досягнути мети. Отож метою нашого уроку є узагальнення та систематизація знань, умінь та навичок з теми «Площі поверхонь та об’єми геометричних тіл».  Тому сьогодні на уроці ми будемо розв’язувати задачі з геометрії прикладного характеру, за допомогою яких розкриваються можливості реалізації зв’язку математичної та професійної підготовки учнів.

 Ви стоїте на порозі закінчення школи. Здавалось би, що після школи математика ніде не пригодиться. На жаль! Тут приходиться використовувати математику ще більше.

Практичні задачі геометричного змісту ─ найактуальніша тема для сьогоднішніх школярів. Ці завдання сприяють застосуванню отриманих знань в реальному житті.

  Уміння вирішувати такі завдання допоможе адаптуватися в суспільстві.

 

 ІІІ. Актуалізація опорних знань

1.Щоб плідно сьогодні працювати, виконаємо завдання на картках. Пропоную завдання:

На малюнку в першому рядку зображено вигляд фігури спереду, а в другому  - вигляд зверху. Визначте що це за фігура.

Відповідь:  1. Конус.    2. Циліндр.      3. Чотирикутна піраміда.

4. Прямокутний паралелепіпед.     5. Трикутна піраміда.            6. Куля.

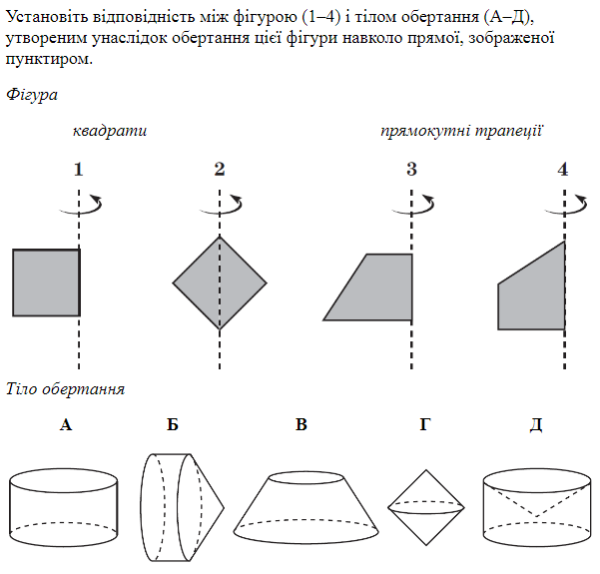2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Відповідь: 1(А),   2 (Г)      3. (В).     4. (Б)

3.  Кожен учень отримує картку із завданням: назва фігури, побудувати зображення цієї фігури, вказати елементи даної фігури, формули для обчислення площі поверхонь та об’єму.

Назва фігури	Зображення	Елементи фігури	Формули для обчислення площі поверхонь та об’єму
Трикутна призма Трикутна піраміда Прямокутний паралелепіпед Зрізаний конус Зрізана піраміда Циліндр Конус Куб

 

• IV. Узагальнення та систематизація знань – 20 хв.

На сьогоднішній урок ви отримали завдання: скласти і розв’язати задачу професійної спрямованості, яка тісно пов’язана з  темою нашого уроку, кожен обирає той напрям,  в якому себе бачить у майбутньому.

Задача 1.

Скільки повних порцій супу міститься в каструлі, яка має форму циліндра, висота якого 40 см, а діаметр 0,3 м. Відомо, що одна порція містить 0,25 л супу.

Дано: V_п =0,25л=250см³;

h=40cм; R=15cм.

Знайти: n – кількість порцій.

     Розв‘язання:

     V===28260 (cм³)

                                           n==113,04113 (порцій)

Відповідь: 113 порцій.

 

Задача 2.    Циліндрична  димова труба  діаметром 65 см має висоту 18 м. скільки жерсті треба для її виготовлення, якщо на заклепку іде 10% матеріалу?

 

Дано: циліндр, d=65см,   H = 18 м  = 18000см,

 Знайти: S_б

                                         Розв’язання:

              S_б =dH = · 65 · 1800 = 117000 см² =

11, 7 м². Але це становить 90% від усієї жерсті.

 

 

 

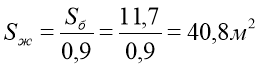
                                          Відповідь: жерсті потрібно взяти 40,8 м² 

 

Задача 3

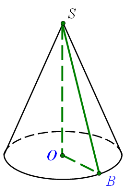
Картоплю насипали в купу конічної форми. Довжина кола основи купи 12 м, твірна -3м.Скільки тонн картоплі знаходиться в купі? Маса 1м³ картоплі 800 кг.

Дано:    конус, С = 12 м, l = 3м.

Знайти:     V_к , m.

Розв’язання:

 

C = 2R.    R = м.

З  трикутника ОВS за т. Піфагора: м.

Об’єм шукаємо за формулою:

м³

 

m = 2,98 · 800 = 2384 кг.

 

Відповідь:2384 кг картоплі в купі.

 

Задача 4.

Скільки мішків аміачної селітри можна помістити в склад розмірами 20м х 9м х 4м, якщо мішок селітри можна прийняти (з певною похибкою) за прямокутний паралелепіпед розмірами 90смх 5смх25см? (На щілини між мішками і центральний прохід виділяється 30% об’єму складу)

 

Дано:    АВСД – прямокутний паралелепіпед, з вимірами  20м х 9м х 4м,

А₁В₁С₁Д₁ – прямокутний паралелепіпед з вимірами 90смх 5смх25см.

Знайти: кількість мішків, n.

Розв’язання:

V₁ = abc = 20 · 9 · 4 = 720 м³.

Перетворимо см у м: 90 см = 0,9м, 5 см = 0,05м, 25 см = 0,25 м.

V₂ = a₂b₂c₂ = 0.9 · 0.05 · 0.25 = 0.0113 м³.

30% об’єму складу становить: 720 · 0,3 = 216 м³.

Об’єм складу з урахуванням вичету 30%: 720 – 216 = 504 м³.

n = 504 : 0,0113 44601

Відповідь: 44601 мішок можна помістити у такий склад.

 

Задача 5.

Фермер вирішив побудувати колодязь циліндричної форми, що має в діаметрі 135 см., А глибину 380 см., Який треба викласти цеглою. Скільки штук цегли йому потрібно купити, якщо розмір цегли 25 X 12 X 6,5 см.

Розв’язання: Довжина кола, діаметр якої менше діаметра колодязя на подвоєну ширину цегли, дорівнює рd ≈ 351 см.

Довжину кола ділимо на довжину цегли, отримуємо 351: 25 ≈ 14 цегли укладено  в   один ряд. Таких рядів буде 380: 6,5 ≈ 59. Отже,  потрібно  цегли   

14 · 59 = 826 штук.

Відповідь: потрібно цегли 826 штук.

Задача 6.

Для поливу висячих садів Семіраміди щодня тисячі рабів качали воду з глибоких колодязів на верхні тераси, а вже звідти по численних каналах вода стікала на нижні тераси. Визначте якою була загальна глибина колодязів, якщо відомо, що радіус цих колодязів 1 м і щодня з них викачували 3 140 м³ води.

Дано: циліндр, R=12 м,   V=3140м,

  Знайти: h

                Розв’язання:

                      Vцил.=ПR² h

                                         h= = 1000 м.

                                        Відповідь:  1000 м

Задача 7.

 Конусоподібний намет висотою 3,5м і діаметром основи 4м покрито тканиною. Скільки тканини пішло на намет?

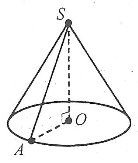Дано: конус, SO = H = 3.5м,  d = 4м.

Знайти:  S_б

Розв’язання:  :  S_б. =

З трикутника АОS: кут О = 90°, за т. Піфагора:

S_б = 3,14 · 2 · 4,03 =25,3 м².

Відповідь: 25,3 м² тканини пішло на намет.

 

Задача 8.

Вважають, що шкідливо залишати на ніч квіти в кімнаті, тому що вони поглинають О₂ , необхідний для дихання людини. Щоб, довести, чи вірна ця думка, обчисліть, до якої величини знизиться вміст кисню у кімнаті розміром 5 м × 3м × 3м за 10 годин внаслідок дихання рослин масою 4 кг і середньою інтенсивність дихання 12 мл О₂ на 1г за добу (умови нормальні). Початковий вміст кисню 21%.

Розв’язання:

Знайдемо об’єм кімнати: V = abc = 5 · 3 · 3 = 45 м³.

У кімнаті об’ємом 45 м³ за нормального тиску міститься 21% О₂ ,

що складає : 45 · 0,21 = 9,45м³.

За 10 годин рослини поглинуть кисню:

12 мл • 4000 г • 10 : 24= 20000 мл = 20л О_{2 =} 0,02 м³ О₂.

Відповідь: кімнатні рослини шкоди диханню людини не завдають.

 

V. Підведення підсумків уроку

      Аналіз діяльності учнів у процесі всього уроку.

 

Я дякую всім вам,  дорогі учні за підготовку до уроку. Закінчити урок хочеться словами  видатного педагога сучасності Василя Сухомлинського:

 «Математика вчить мислити й разом з тим вселяє віру в безмежні сили людського розуму . Вона виховує волю, характер».

                                                                  В.О. Сухомлинський

Запитання до класу:

1. Що сподобалося на сьогоднішньому уроці?

2. Об‘єми яких геометричних тіл ми знаходили?

3. Як знайти об‘єм куба?

4. Як знайти об‘єм паралелепіпеда?

5. Як знайти об‘єм піраміди?

6. За якою формулою обчислюється об‘єм циліндра?

   5.2.  Повідомлення та обґрунтування оцінок.

VI. Домашнє завдання

Завдання початкового і середнього рівнів:

 

№1

 

№2

 

№3. Завдання достатнього рівня:

 

 

 

 

№4. Завдання високого рівня: