Урок "Розв'язування прикладних задач за допомогою прогресії." 9 клас.

Алгебра,9 клас.

Тема уроку: Розв’язування прикладних задач за допомогою прогресії.

Мета:

• повторити та узагальнити знання учнів з теми;
• удосконалити й систематизувати вміння і навички учнів  застосовувати знання до розв’язування  прикладних задач; 
• розвивати пізнавальну та інформаційну компетентність, логічне, самостійне, творче мислення, навички самоконтролю і взаємоконтролю;
• виховувати увагу, спостережливість, самостійність, кмітливість.

Тип уроку: узагальнення і систематизація знань, умінь і навичок.

Обладнання : комп’ютер, мультимедійна дошка, презентація у PowerPoint.

                                                                             Епіграф:

«Недостатньо володіти мудрістю,

треба вміти користуватися нею.»

                                                                                                                  Цицерон.

Хід уроку:

1.Організація  класу. Мотивація навчальної діяльності.

Сьогодні на уроці ми підсумуємо вивчення однієї з найцікавіших тем математики – прогресії. Їх внутрішня гармонія, строга витончена краса роблять теорію арифметичної і геометричної прогресії відображенням фундаментальних властивостей  об’єктивного світу, що існує незалежно від нас, нашої свідомості. На сьогоднішньому уроці ми узагальнюватимемо знання з цієї теми і  будемо використовувати  їх при розв’язуванні різних прикладних задач.

2. Перевірка домашнього завдання.

3. Актуалізація опорних знань.

           Запитання:

1. Арифметична прогресія -...

2. Геометрична прогресія -...

3.У геометричній прогресії перший член 8 , другий член 4 . Знайдіть знаменник ?

4.У арифметичній прогресії перший член 9 , другий член 3 . Знайдіть різницю арифметичної прогресії.

5. Властивості арифметичної прогресії:

6.Чи є послідовність степенів числа 2  геометричною прогресією?

7. Властивості геометричної прогресії:

8. Знаменник геометричної прогресії обчислюється за формулою...

9 . Формула п-го члена арифметичної прогресії така…

10. Формула п-го члена геометричної прогресії така…

11. Сума п перших членів арифметичної прогресії

12. Сума п перших членів геометричної прогресії.

4. Самостійна робота з взаємною перевіркою.

1).Вказати перший член і різницю арифметичної прогресії:

Варіант І   3 ; 8; 13;…   Варіант ІІ   3; 7; 11;…                                                  А)3; 4   Б) 3; 10   В) 13; 8  Г) 3; 5

2).Знайдіть одинадцятий член арифметичної прогресії:

 Варіант І    2; 5; 8;…        Варіант ІІ    3; 5; 7; …                                             А)35   Б) 25   В) 23     Г) 32

3).Укажіть знаменник геометричної прогресії :

Варіант І    8; 4; 2;…         Варіант ІІ    10; 2; 0,4; …                                        А)0,1   Б) 0,2   В) 0,4   Г) 0,5

4).Знайдіть четвертий член геометричної прогресії, якщо:

 

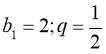
Варіант І                             Варіант ІІ                          

            

                             А) 0,25     Б) 3    В) 1/3        Г) 4

 

5).Чи є членом арифметичної прогресії -3; -8; -13; … число

                       Варіант І    -160                  Варіант ІІ    -153

6). Знайдіть суму членів геометричної прогресі, якщо :

 

Варіант І                                                    Варіант ІІ

          

5. Розв’язування  задач прикладного характеру.

Задача 1.

Кількість еритроцитів(з розрахунку на 1 ) в крові людини становить на рівні моря – 5 млн. Через кожні 6оо м  підняття  вгору їх кількість збільшується на 1 млн.

Скільки еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест (4800  м)? Чому це відбувається?

Розв’язання:

За умовою задачі отримуємо арифметичну прогресію.

, , 4800:600=8,  ,  5+7=12.

Відповідь: 12 млн. еритроцитів.

У зв’язку  з розрідженим повітрям в легені повинно більше потрапити  кисню відповідно цьому збільшується кількість еритроцитів.

Задача 2.

Бактерія,  потрапивши в організм, до кінця 20-ї хвилини ділиться на дві, кожна з них до кінця 20-ї хвилини знов ділиться на дві і т.д. Скільки  бактерій стане в організмі через добу?

Розв’язання:

1 доба=24 год; 24 год=1440 хв.; 1440:20=72.

За умовою задачі отримуємо геометричну прогресію: 1;2; 4; 8;…; =1, =2.

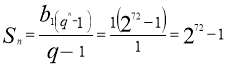(бактерії) .

Відповідь: в організмі за добу буде  бактерій.

Коментар учня.

Інтенсивність розмноження бактерій використовують:

 В харчовій  промисловості (при виготовленні напоїв, кисломолочних продуктів, квашенні, соленій; в  фармацевтичній промисловості (при виготовленні ліків, вакцин); в сільському господарстві(при виготовленні кормів для  тварин); в комунальному господарстві і природоохоронних   заходів (при очищення стічних вод,  ліквідації нафтових  плям).

Задача 3.

Уявіть, що ви хочете взяти у борг 3000 гривень. За перший день ви будете  зобов’язані заплатити кредитору 1 копійку, за другий  2 копійки, за третій – 4 копійки і т.д. Чи укладете ви угоду з кредитором не менше,  ніж на 20 днів?

Розв’язання:

Математична модель – геометрична прогресія,    =1 ,   q=2.

1048576 коп. = 10485,76 грн.

Висновок: укладання угоди на таких умовах  задає матеріального збитку на суму 7485,76 грн.

Коментар вчителя:

Уявіть  собі, що ви відкрили в банку рахунок у сумі    грн. під p % річних на n років. У вас є дві стратегії поведінки: або в кінці кожного року зберігання вкладу знімати відсотки по рахунку, тобто отриманий прибуток у розмірі 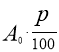   грн., або прийти в банк один раз в кінці зберігання вкладу. Який дохід ви отримаєте в тому чи іншому випадку?

В першому випадку при  n=1  ви  отримаєте 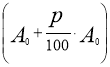    грн., при n=2  ваша підсумкова сума становить  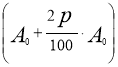 грн., при  n=3   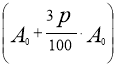грн. і т. д.

Математична модель ситуації – скінчена   арифметична прогресія

, , , , …, .

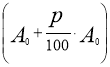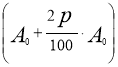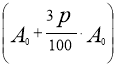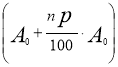При першої стратегії за n років ви отримаєте

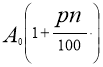грн.   –формула  складних відсотків.

 Якщо ви прийняли рішення прийти в банк тільки в кінці строку зберігання грошей вкладу, то при n=1 сума вкладу становить , як і в першому випадку

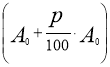грн., тобто  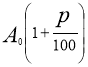  грн., тобто сума вкладу збільшиться у  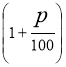  разів. В стільки ж  разів сума вкладу збільшиться і к кінцю другого року зберігання вкладу, і к кінцю третього року зберігання вкладу і т.д.

Математична модель ситуації -   скінчена  геометрична прогресія

, , , ,…,.

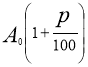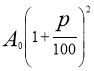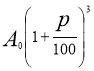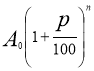При другої стратегії за  n  років ви отримаєте 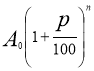   грн. - формула складних відсотків.

Задача 4.

Нехай вклад  становить  10000 грн.,  банк нараховує 10% річних, строк зберігання вкладу – 5 років. Порахуйте скільки грошей  буде на рахунку вкладника при стратегії простих відсотків и стратегії складних відсотків за допомогою  прогресії.

Розв’язання:

Вклад 10000 грн., 10% річних, строк зберігання 5 років.

Стратегія простих відсотків.

Математична модель – арифметична прогресія.

=100000, d=1000 грн,

=+5d= 100000+5*1000=15000 (грн.)

Стратегія складних відсотків.

Математична модель геометрична прогресія.

=100000,  =1+0,1=1,1,

10000=16105,1 грн.

6. Самостійна робота. Розв’язування задач прикладного характеру.

Варіант 1.

1).Підприємець взяв у банку кредит на суму 50000 грн. під 15% річних. Яку суму повинен повернути підприємець банку через 3 роки?

2).При кожному діленні амеби з’являється  дві нових амеби. Скільки амеб буде після 6  ділень, після 10 ділень.

3).Тіло, яке вільно падає, проходить за перу секунду 4,9  м, а за кожну наступну – на 9,8  м більше, ніж за попередню. Встановити, скільки секунд падатиме тіло з висоти 1960  м?

Варіант 2.

1). На вкладі у банку  знаходиться  50000 грн. Скільки відсотків нараховує банк щорічно, якщо через 2 роки сума на вкладі становить 68445 грн.?

2). Гідра розмножується брунькуванням, причому при кожному діленні виходить 5 нових особин. Яка кількість ділень необхідна для здобуття 625 особин?

3).Після кожного руху поршня розріджувального  насосу з посудини забирається 5% наявного в ній повітря. Визначте тиск повітря в середині посудини після десяти рухів поршню, якщо початковий тиск був 760  мм рт. ст..

7.Підведення підсумків уроку. Домашнє завдання.

Виставлення оцінок учням.

Інтерактивна технологія «Незакінчені речення»

На сьогоднішньому уроці я дізнався…

На сьогоднішньому уроці найважливішим відкриттям для мене було…

На початку уроку я поставив перед собою мету. Ось як я її досягнув…

8. Додаткова інформація

Арифметичну прогресію можна зустріти в літературі. Згадаємо віршові розміри: ямб, хорей, дактиль, амфібрахій, і анапест. Відмінність між ними в кількості стоп і в різних розташуваннях наголошених складів вірша.

• Ямб – у слабо-тонічному віршуванні двоскладова стопа з наголосом на парних складах вірша, тобто наголошеними є 2-й, 4-й, 6-й, 8-й і т.д. склади. Номери наголошених складів утворюють арифметичну прогресію з першим членом 2 і з різницею, рівною 2:     2, 4, 6, 8, 10…

Ста/рі/  ду/би, спа/си/бі/ вам /за /о/сінь,

за/ від/лі/та/ння ра/до/сті /і /птиць.

Ще/, пев/но, я/  за/тур/ка/на  не/ зов/сім,

Що/ чу/ю  шур/хіт/  кня/жих  баг/ря/ниць

                              (Ліна Костенко)

• Хорей – у слабо-тонічному віршуванні двоскладова стопа з наголосом на непарних складах вірша. Номери наголошених складів утворюють арифметичну прогресію, перший член якої дорівнює 1, а різниця дорівнює 2:  1, 3, 5, 7, 9…