Урок "Розв'язування систем рівнянь другого степеня з двома змінними"

9 клас

Інтегрований урок алгебра – інформатика

 

РОЗВ’ЯЗУВАННЯ  СИСТЕМ  РІВНЯНЬ ДРУГОГО СТЕПЕНЯ З  ДВОМА  ЗМІННИМИ

 

 

 Учитель математики                                                                                                                «спеціаліст вищої категорії»

Старший вчитель

Т.В.Станкевич

 Брилівський ЗПЗСО

Олешківського району

Херсонської області

 

 

. Мета:  формувати уміння розв’язувати системи рівнянь другого степеня з

двома змінними різними способами: графічним , додавання ,

підстановкою;

розвивати логічне мислення , пам'ять , увагу, уміння аналізувати і

систематизувати знання , сприяти вдосконаленню навичок роботи з

комп’ютером, з програмним забезпеченням «Терм 7-9»;

виховувати  наполегливість у роботі , взаємоповагу, почуття

відповідальності за свої вчинки, почуття патріотизму.

 

Тип уроку: урок формування вмінь і навичок

 

Обладнання: комп’ютери, ППЗ « Терм 7- 9 », роздатковий матеріал, DVD ,

плакат «Дерево очікувань» з набором жовтих і зелених листочків,

геометричні  фігури : 4 ромби, 4 квадрати, 4 прямокутники,

4 паралелограми

кольору зелений (високий), жовтий (достатній), блакитний (достатній), рожевий (середній).

.

 

Епіграф: Найкращий спосіб вивчити що-небудь  - це відкрити його самому.

                                              Хронометраж  уроку.

І.Перевірка домашнього завдання (5 хв).

ІІ. Повідомлення теми уроку (3 хв).

ІІІ. Мотивація навчальної діяльності (2 хв).

ІV. Актуалізація опорних знань у вигляді інтерактивного методу «Акваріум» (10 хв).

V.Пояснення матеріалу.(3 хв).

VІ. Осмислення і усвідомлення матеріалу.(19 хв).

VІІ. Підсумок уроку (3 хв).

 

Хід уроку

І. Перевірка домашнього завдання.

Учитель математики:

1. Перед уроком консультанти перевіряють стан виконання домашнього завдання.

Вчитель виясняє які запитання по домашньому завданні. Якщо є ,то спочатку дає змогу учням відповісти.

В кінці уроку учні здадуть зошити для перевірки домашнього завдання і класної роботи.

 

2.Усне опитування у вигляді «Бліц - турніру», «Факт чи вигадка»

( всі учні беруть участь сигналізуючи: «так» - зелений, «ні» - жовтий листочки).

 

З а п и т а н н я  т у р н і р у

 

1. Функція у = ах² + в – квадратична (так) .

2. Графіком функції у = ах² є гіпербола (ні).

3. Якщо коефіцієнт при х² більше нуля , то вітки параболи напрямлені вниз (ні).

4. Скільки ви знаєте способів побудови графіків квадратичних функцій 1,2,3?(3)

5. Функція у = ах² + вх + с, де а,в,с- деякі числа , що дорівнюють нулю є квадратичною (ні).

6. Функція зростає, якщо більшому значенню аргументу відповідає більше значення функції (так).

7. Область визначення функції у = ах² + вх + с всі дійсні числа (так).

8. Область значень функції у = 2х – 4 є проміжок (о; +∞) (ні).

9. У квадратичній функції у = ах² +вх+с , коефіцієнт в визначає розташування віток параболи «вниз», «вгору» (ні).

 

ІІ. Повідомлення теми уроку.

Учитель математики

Розв’язування систем рівнянь другого степеня з двома змінними.

- Що ви очікуєте від цього уроку?

(можливі відповіді учнів : мені цікаво які завдання будемо виконувати на комп’ютері , хочу дізнатися щось нове, хочу навчитися розв’язувати такі системи, і т. д.)

 

ІІІ. Мотивація навчальної  діяльності.

 

  

   Учитель математики

   Теорія систем рівнянь має багатовікову історію. Із задачами лінійного характеру ми зустрічаємось в житті на кожному кроці. Багато задач пов’язані з визначенням залежностей однієї величини від кількох факторів. Для математичного опису такої залежності можуть бути функції від кількох змінних.

    З такими залежностями ми зустрічаємося в механіці, динаміці, електриці, у плануванні і управлінні виробництвом. Наприклад: (задачі економічного змісту).

 

1. Фірма – монополіст випускає 26 одиниць товару (рукавиці, валянки, чоботи, шкарпетки, шапки,…), який користується різним попитом у різних прошарків (сільське, міське) населення. Після дослідження менеджери визначили обсяг виробництва, за якого фірма максимізує прибутки і величину свого прибутку.

2. Землевласник має у своєму розпорядженні ділянку землі і може здавати в оренду для сільськогосподарського виробництва. Можна визначити економічну ренту , а також дохід достатній для того, щоб земля залишалася в сільськогосподарському використанні.

 

ІV. Актуалізація опорних знань у вигляді інтерактивного методу «Акваріум».

Учитель математики

 Група сідає в «акваріум», отримує завдання:

• читає вголос завдання;
• обговорює його в групі, використовуючи метод дискусії;
• дійти до спільного рішення за 1-2 хв.

 Учні класу слухають не втручаючись, а тоді аналізують відповіді за планом:

- Чи погоджуєтесь з думкою групи?

- Чи була ця думка достатньо аргументована, доведена?

- Яку з думок ви вважаєте найбільш аргументованою?

Поперед класу стоїть стіл зі стільцями – це «акваріум». На столі лежать

намальовані рибки, до яких прикріплені питання.

Кожному учневі на початку уроку роздаю бейджики із фігурками певного

кольору. Запросити учнів розділитися за  групами геометричних фігур. Квадрат – високий рівень, Прямокутник – достатній, а ромб – середній.

       Учитель запрошує по черзі групи до «акваріуму». Вони беруть одну рибку, на якій вказано номер завдання. Всі завдання транслюються через DVD на телевізор у вигляді слайдів.

 

З а в д а н н я   г р у п а м

 

1. В чому полягає графічний спосіб розв’язування систем рівнянь?

Як розв’язати графічно систему рівнянь    у –х =4,

                                                                        у +х =2.  ?

2. Поясніть на прикладі зміст способу   підстановки    х – у =1,

                                                                                             х ∙ у =20.

3.Виконати презентацію функцій , які представлені у вигляді слайдів і демонструються через  DVD.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

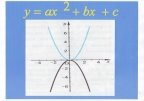
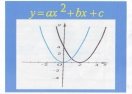
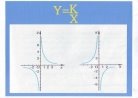
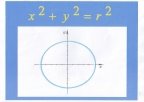
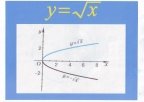
4.  Як розв’язують системи рівнянь способом додавання?

Поясніть на прикладі    х + у = 3

                                              х – у =1.

 V. Пояснення матеріалу.

Учитель математики

   -  Наведіть приклади рівнянь другого степеня з двома змінними .

(Учні наводять приклади , а вчитель записує їх на дошці.)

• Як ви гадаєте, яка система називається системою рівнянь другого степеня

з двома змінними?

• (Очікувана відповідь). Якщо одне рівняння системи другого степеня, а

друге з тими самими змінними другого або першого степеня, то таку систему називають системою двох рівнянь другого степеня з двома змінними.

 -  Розв’язують їх такими ж способами як і системи лінійних рівнянь з двома змінними, тобто…(учні повторюють способи розв’язування систем рівнянь).

 

VІ. Осмислення і усвідомлення матеріалу

  Учитель математики:

Прошу учнів сісти за кольором: зелений (високий), жовтий (достатній), блакитний (достатній), рожевий (середній).

Учитель інформатики. Завдання будемо виконувати, використовуючи комп’ютер. Однією з галузей математики є комп’ютерна алгебра, яка орієнтована на використання ЕОМ для виконання аналітичних перетворень математичних виразів.

Складаються програмові системи, що використовуються під час розв’язування задач з космосу, теоретичної фізики і т.д. Першу в Європі швидкодіючу машину створено у Києві у 1951 р. під керівництвом академіка С.О.Лебедєва.

 

Учитель математики.На столах лежать завдання по рівнях.

 

З р а з к и   з а в д а н ь

 

Високий рівень

 

1. Розв’язати  графічно систему рівнянь.

 

а)      х ²    – 4х + у ² = 0                     х²  + у ² +   6х + 8у = 4

    х – у = 0                                     у = (х+2) (х+4)

 

 

2. Розв’язати систему рівнянь способом підстановки.

 

б)      х ²    + 2ху + у ² – х – у  = 30

         х + 2у = 3                                    

3. Розв’язати систему рівнянь спочатку способом додавання, а потім підстановки.

         ху + х + 2у = 7

 ху + х + 3у = 13

 

4. Розв’язати систему рівнянь із трьома невідомими.

х + у = 1

у + z = 2

х z = 6

 

5. Розв’язати систему рівнянь способом введення нових змінних.

х + у + ху = 11

х у (х + у) = 30

 

Достатній рівень

 

1. Розв’язати  графічно систему рівнянь.

а)    у = х ² + 4х б)    у = 2 (х – 1)² + 4  в)    (х + 4) ² + (у – 3) ² = 9

х + у = - 4        х у = - 12    х – у = - 4

 

2. Розв’язати систему рівнянь способом підстановки.

а)   3 х ² – ху = 1 б )    х + у = 8

  3х + у = 5                  х ² + у ² = 16 + 2ху

 

3. Розв’язати ситему рівнянь способом додавання.

а)    х ² – у = 7 б)      х ² + у  = 7 в )    1/х + 1/у = 8/15

       х ² + у = 11                3х ² + 2у = 18                   1/х - 1/у = 2/15.

 

Середній  рівень

 

1. Розв’язати  графічно систему рівнянь.

а)    у = х ²                        б)      у = х ²                                             в)    х ² + у ² = 9

у = 2х х + у = 2 у = х + 3

 

2. Розв’язати ситему рівнянь способом додавання.

а)    у = 4х                                      б)      х + у ²  = 7                                          

х ² + у  + 3 = 0                    х у = 10 

 

3. Розв’язати систему рівнянь способом підстановки.

а)   х + у ² = 3 х + у ² = 7

 х - у ² = 1 2х - у ² = 2

 

(Групи обговорюють завдання і за командою вчителя сідають за комп’ютери виконувати перше завдання, використовуючи програму «Терм 7-9»)

Учитель інформатики:

1. Виконаємо персоніфікацію.
2. Входимо в програму «Графіки».
3. Відкриваємо розділ «Рівняння – графіки».
4. Будуємо графік, натиснувши клавішу ∆.
5. Аналогічно будуємо графік другого рівняння.
6. Знаходимо точки перетину графіків.

Робота в парах. Один учень виконує завдання а), а другий – завдання б). Учні високого рівня можуть отримати підказки щодо розв’язання у « Зошиті».

Розв’язання записане у «Зошиті».

 

1. а) З першого рівняння виділити квадрат двочлена для змінної х.

(х – 2)² + у ² = 4

б) В першому рівнянні виділити квадрат двочлена для змінних х і у

 друге рівняння записати у вигляді у = ах ² + вх + с.

   (х + 3)² + (у+4)² = 25

  у = х ² + 6х + 8

2. Виразити з першого рівняння змінну х через у, підставити у перше рівняння.

   х = 3 – 2у

   у ² – 5у ² – 24 = 0        Відповідь. (- 13;8), (9; - 3)

3. Додамо обидва рівняння попередньо помноживши рівняння на  - 3.

   2х + 3у = 8

   ху + х + 2у = 7

З другого рівняння виражаємо х через у і підставимо у перше рівняння.

   х = 7 – 2у

          у + 1

   у ² – 3у + 2 = 0           Відповідь. (1; 2,5), (1; 2).

4. З першого рівняння виразимо х через у. З другого рівняння виразимо z

через у. Підставимо у третє рівняння.

   х = 1 – у

   z = 2 – у

   (1 – у)(1 – у) = 6            Відповідь.(- 3; 4; - 2), (2; - 1; 3).

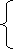5. Вводимо заміну ху = а, х + у = в.

   в + а = 11                       За теоремою Вієта: а = 5, в = 6, або а = 6, в = 5

  ав = 30

Відповідь. (1; 5), (5; 1), (2; 3), (3; 2).

 

Учитель математики оцінює роботу учнів, роздаючи жетони різного кольору по рівнях. Зелені жетони- високий рівень, блакитні –достатній, рожеві – середній.

VІІ. Підсумок уроку

   Рефлексія.

• Чи справдились ваші очікування?
• Підійдіть до дерева і причепіть листочки: зелені – «все зрозуміло», жовті –

«щось не зрозуміло». Попередньо на листках напишіть своє прізвище. 

• Здайте зошити.

Підсумок успіхів учнів. Ті, хто одержали по три жетони одержує оцінку свого рівня. Високий рівень - за 5 завдань.

 

Домашнє завдання. Повторити п. 24,25,37.

 Рівень А: 169а, 175а, 178 (усно).

 Рівень Б: 178 (усно), 179а, 180.

 Рівень В: індивідуально.

Розв’язати систему рівнянь:

а) графічним способом     у = 2 (х – 1)² + 3,

  у х = 10.

 

б) способом підстановки    х + у = 8,

    х ² + у ² =16 + 2ху.

в) способом додавання    1/х + 1/у = 8/15,

 1/х - 1/у = 2/15.

 

Література.

1. Капіносов А.М. Тематичне оцінювання. Алгебра 9 клас: Навчальний посібник для 9 – го класу. – Дніпропетровськ: Інновація, 2005.
2. Олімпіадні завдання з економіки: Збірник /О.В..Олійник, І.Є.Тимченко. – Х.: Веста: Вид-во «Ранок», 2007. – 4000с.
3. Підручник «Алгебра 7 – 9 клас» Т.П. Бевз.