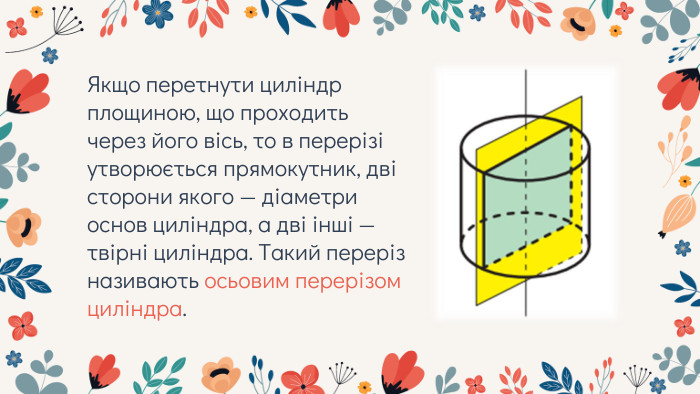
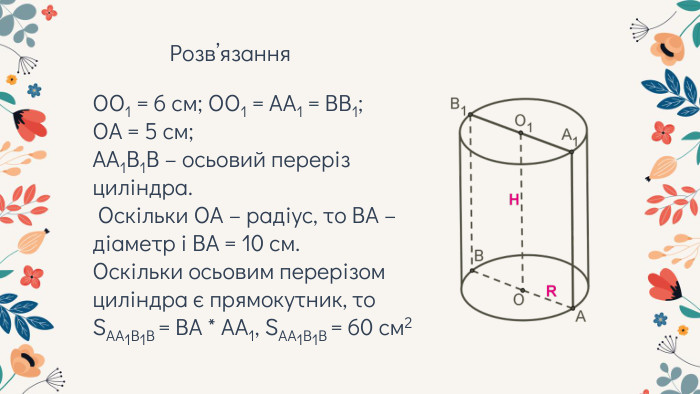
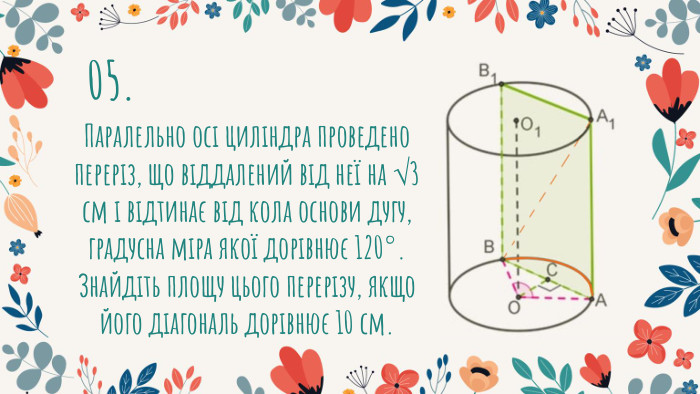
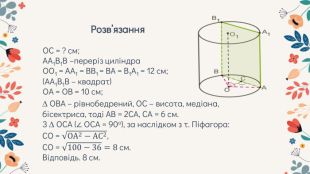
Урок розв'язування задач на переріз циліндра
Про матеріал
Матеріал містить теоретичні відомості та розв'язки деяких задач з теми "Переріз циліндра" за підручником авторства Мерзляк для 11 класу Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку