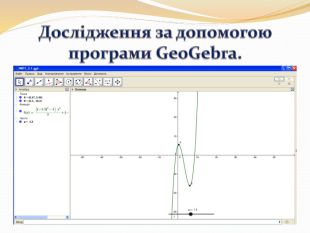
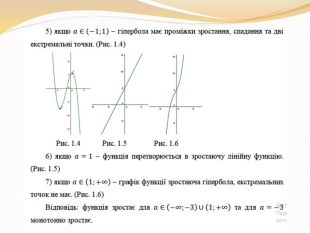
Функції та їхні графіки на факультативних заняттях з математики
Про матеріал
В сучасній освіті комп’ютерна техніка та Інтернет широко використовуються не тільки для навчання інформатики, але і для навчання інших предметів. Необхідність комп’ютерної підтримки освітнього процесу визначається сьогодні швидким розвитком інформаційних та комунікаційних технологій, проникненням їх у всі сфери життя, в тому числі і в сферу навчання, що обґрунтовує актуальність роботи. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку