Урок "Розв’язування задач на використання теореми Піфагора"

Тема. Розв’язування задач на використання теореми Піфагора

Мета. Закріпити теоретичні знання, формувати вміння та навички учнів розв’язувати практичні задачі на застосування теореми Піфагора, активізувати пізнавальну діяльність учнів; розвивати логічне мислення, пам'ять, спостережливість; виховувати активність, прищеплювати інтерес до геометрії. Формувати зв’язне мовлення.

     Обладнання: комп'ютерна презентація Microsoft PowerPoint, картки із завданнями.

     Тип уроку: узагальнення і систематизації знань, вмінь та навичок учнів.

ХІД УРОКУ

I. Організаційний момент.

- Діти, яку тему ми вивчаємо? (Ми вивчаємо теорему Піфагора).

- Що було на домашнє завдання?

- Для якого трикутника виконується теорема Піфагора?

- А зараз перевіримо, як ви знаєте прямокутний трикутник.

II. Актуалізація опорних знань учнів.

      Розгадування кросворду:

1.Як називається трикутник, у якого є прямий кут?

2. Які ще кути, крім прямого, може мати прямокутний трикутник?

3. Теорему Піфагора можна записати за допомогою …

4. Як називаються сторони прямокутного трикутника, що утворюють прямий кут?

5. Як називається найбільша сторона прямокутного трикутника?

6. У трикутнику можна провести …

7. Що можна знайти за допомогою теореми Піфагора?

 

- Діти, яке слово ми отримали? (Піфагор)

- Хто такий Піфагор?

- Сформулювати теорему Піфагора.

III. Мотивація навчальної діяльності учнів.  

      На попередньому уроці за допомогою теореми Піфагора ви вчилися знаходити невідомі сторони прямокутного трикутника. Ви вже знаєте, що  для побудови прямого кута, теорему Піфагора використовували  ще у Стародавньому Єгипті. Сьогодні на уроці ми розглянемо деякі приклади  застосування теореми Піфагора у сучасному житті.

        Відкрили зошити. Записали тему уроку «Розв’язування задач».

ІV. Розв’язування задач.   

Усно: Знайти невідому сторону.  

 

                                    а            х-?                                   с                    в

    а             с

                                                в                                          х - ?                 

  х - ?

    У класі є багато хлопчиків. Можливо, у майбутньому, хтось із вас буде столяром, буде мати справу із деревиною. Хочу запропонувати вам таку задачу.

 

 Задача.  Діаметр колоди дорівнює 12 см. Чи можна з цієї колоди витесати квадратний брус із ребром:

а) 10 см; б) 8 см?

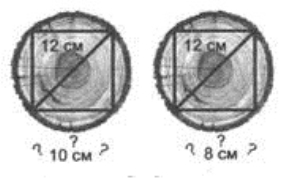
Розв'язання

- Спочатку формулюємо задачу мовою математики.

- Яку фігуру будемо розглядати? (квадрат)

- Що ми знаємо про квадрат? (рівні сторони)

- Що проведено у квадраті? (діагональ)

- Які фігури утворилися?

- Щоб дати відповідь на запитання задачі, яку фігуру потрібно розглянути?

1.  а = 10см

 (см).

2.  а = 8см        

  (см).

Відповідь. а) Ні; б) так.

- А зараз трохи позмагаємося. Гра “Хто швидше?”(дві команди по 4 учні).         1 учень. Намалювати прямокутний трикутник.

2 учень. Позначити прямокутний трикутник.

3 учень. Записати теорему Піфагора для заданого трикутника.

4 учень.  Записати рівності, які випливають з теореми Піфагора.

Задача 886 (робота з підручником).

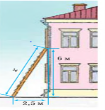
            1) Якої довжини має бути драбина, щоб її можна було приставити до вікна, розташованого на висоті 6 м, коли відстань від нижнього кінця драбини до будинку має дорівнювати 2,5 м?

                                                                                                                     

- З чого почнемо розв’язувати задачу?

- Який малюнок підходить до нашої задачі?

 

                  А             Дано: ΔАВС – прямокутний

                                  СВ = 2,5м, АС = 6м

                                  Знайти: АВ

 

 

 В              С

Розв’язання.

1. АВ² = АС² + СВ² = 6² + 2,5² = 36 + 6,25 = 42,25(м²);

2. АВ = = 6,5 (м).

- Для чого може бути потрібна драбина?

( Для різних надзвичайних ситуацій, при потребі телефонувати за номером 101).

 

Самостійна робота.

Варіант-І

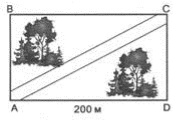
 Задача.  Парк має форму прямокутника. Довжина однієї з його сторін дорівнює 200 м, а площа — 72000 м². Яка довжина головної алеї парку, що проходить по його діагоналі.

 

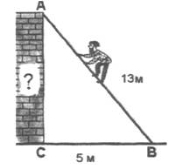
Варіант-ІІ

Задача.  Знайти висоту будівлі.

 Індивідуальна робота з  учнем.

                                             - Яку фігуру ми вивчаємо?

                                             - Як називаються сторони прямокутного трикутника?

 

V.Підведення підсумків уроку.

 

Бліцопитування 

• Чи можна застосувати теорему Піфагора до тупокутного трикутника?
• Сформулювати теорему Піфагора.  

        -   Як знайти невідомий катет?

       -   У прямокутному трикутнику, якщо є дві сторони, завжди можна

           знайти …

Оцінювання учнів.

Домашнє завдання.