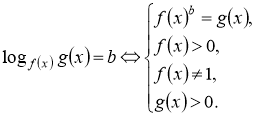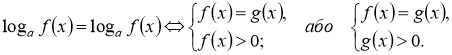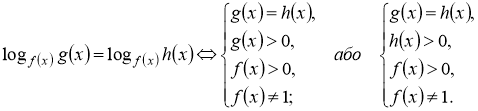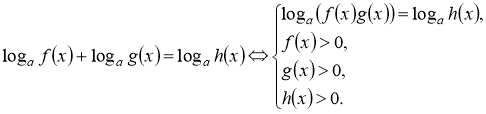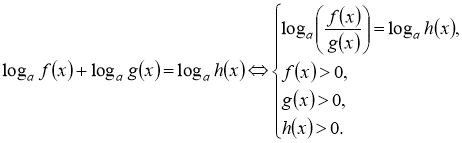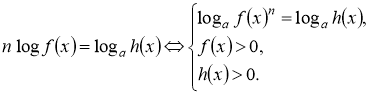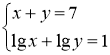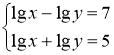Урок " Логарифмічна функція"

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

УРОК 3

 

Тема: Логарифмічні рівняння.

Мета: Формування в учнів навичок і вмінь розв’язувати найпростіші логарифмічні рівняння та ті, що зводяться до них безпосереднім застосуванням властивостей логарифмів.

Обладнання: таблиця основних властивостей логарифмів.

 

Хід уроку.

 

І. Повторення попереднього матеріалу. Запропонування учням зобразити схематично графіки функцій і , пояснити властивості цих графіків.

У цей час переглянути наявність виконаного домашнього завдання в учнів і зробити зауваження щодо по будови графіків.

 

ІІ. Пояснення нового матеріалу.

Фронтальне опитування.

 

1. Дати означення логарифма числа.

Обчислити:	1)	6)
	2)	7)
	3)	8)
	4)	9)
	5)	10)

 

2. За допомогою основної логарифмічної тотожності зробити необхідні обчислення, визначивши слово-код свого варіанта (двоє учнів виконують завдання на відкидних дошках, а учні на своїх місцях по варіантам)

 

Варіант І	Варіант ІІ
1)	1)
2)	2)
3)	3)
4)	4)
5)	5)

 

 

 

Дешифратор.

 

							Відповіді:	В1 – «Сокол»
Л	Й	С	О	А	К			В2 – «Скала»

 

3. Сформулювати властивості логарифмів добутку, частки, степеня. Записати на дошці ці властивості.

 

4. У чому полягає властивість оборотності функції?

Повідомити тему і мету уроку.

Рівняння із змінною під знаком логарифма або в основі логарифма називаються логарифмічними.

 

Основні методи розв’язання логарифмічних рівнянь

 

1)

2)

3)

4)

5)

6)

7)

Розв’язати логарифмічне рівняння – означає знайти всі його корені або довести, що рівняння коренів не має.

У процесі розв’язання логарифмічних рівнянь користуються властивостями логарифмічної функції та означенням логарифма. Найпростіше логарифмічне рівняння має вигляд , де , , . За означенням логарифма випливає, що .

Інший вигляд найпростішого логарифмічного рівняння такий:

 

,

 

де , , , . З цього рівняння випливає, що . Це можна обґрунтувати на підставі означення логарифма: .

Також найпростішим логарифмічним рівнянням є рівняння: , де , , . З означення логарифма маємо: , .

Усі види логарифмічних рівнянь зводяться до найпростіших тотожними перетвореннями виразів з логарифмами.

 

Колективне розв’язання прикладів:

 

а)	в)
б)	г)

 

Кожному учню видати таблицю методів розв’язання логарифмічних рівнянь і відповісти на незрозумілі етапи розв’язання.

Під областю визначення рівняння розуміють множину значень змінної, при яких обидві частини рівняння мають зміст.

При перетвореннях логарифмічного рівняння його область визначення може змінюватися і нове рівняння може бути не рівносильним вихідному. Якщо область визначення нового рівняння розширилася, то воно є наслідковим вихідного рівняння і при розв’язуванні його можуть з’явитися сторонні корені, які не задовольнятимуть дане рівняння. Їх легко виявити за допомогою підстановки у вихідне рівняння або в умову, що виражає область визначення вихідного рівняння.

 

Колективне розв’язання рівнянь.

 

.

 

Із рівності логарифмів чисел випливає: і дане рівняння має зміст, якщо і .

При зміні даного рівняння область визначення розширилася, і знайдені корені потребують перевірки.

Розв’яжемо рівняння.

, , , .

Перевіримо одержані корені підстановкою їх в умову, що визначає область визначення даного рівняння: . , - сторонній корінь.

Отже, - корінь даного рівняння.

Далі з учнями класу розв’язати № 52 (1, 3, 7), № 54 (1).

 

Підсумок уроку.

 

Засвоїли обґрунтування розв’язання найпростіших логарифмічних рівнянь. Ознайомилися з умовами виникнення зайвих коренів, навчилися розв’язувати деякі логарифмічні рівняння зведенням їх до найпростіших шляхом застосування властивостей логарифмів.

 

Д/З § 3 (розділ V), запитання 26-27, № 52 (2, 4, 5), № 54 (2).

 

 

УРОК 4

 

Тема: Розв’язання логарифмічних рівнянь.

Мета: Формування в учнів навичок і вмінь розв’язувати логарифмічні рівняння, що зводяться до квадрат, і за допомогою формули переходу до іншої основи логарифмів.

Обладнання: таблиця основних властивостей логарифмів.

 

Хід уроку.

 

І. Повторення попереднього матеріалу. Два учні на дошках відтворюють розв’язання завдань № 52 (5) і 54 (2). В цей час з учнями розбираємо запитання 26-29.

Обговорення результату роботи на дошці.

Виконати учням тестове завдання:

1. При якому значенні ?

    а) 5; б) 9; в) 8; г) -9; д) 7.

2. Вказати число, яке є коренем рівняння .

    а) 1; б) -1; в) 2; г) -2; д) 0.

3 Розв’язати рівняння:

    1) .

         а) 3; б) 4; в) 2; г) 5; д) -4.

    2) .

         а) 0; б) 1; в) -1; г) 8; д) -8.

    3).

         а) 1; б) -1; в) 0; г) 2; д) -2.

    4) .

         а) 0; б) 1; в) ; г) ; д) .

Завдання виконується на окремих аркушах і здається вчителює

Повідомляється тема і мета уроку.

 

ІІ. Розв’язання логарифмічних рівнянь

1. Колективно розв’язуємо рівняння, яке зводиться до квадратного.

 

.

 

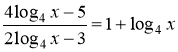Зразок оформлення розв’язання.

 

,

,

,

,

,	,
.	.

 

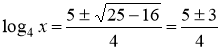Перевірка.

 

 

 

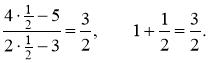
Відповідь: , .

 

2. Розв’язати № 53 (7) за зразком.

 

3. Метод зведення логарифмів до однієї і тієї ж основи.

 

.

 

Область визначення в рівнянні знаходимо з умови

 

, .

 

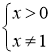Перейдемо до основи .

 

,

 

,

 

,

 

,

 

,

 

,	,
.	.

 

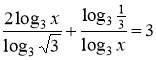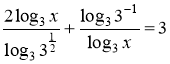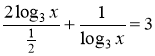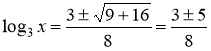В області визначення рівносильність не порушилась, тому сторонніх коренів немає.

Відповідь: ;

 

4. Самостійно розв’язати рівняння

.

Колективно з’ясувати до якої основи зручно перейти при роз’язанні рівняння.

 

5. Метод логарифмування.

Розв’язати рівняння .

Про логарифмуємо обидві частини рівності , одержимо:

,	,	,	або	,
		.		.

Перевірка: ,

.

Відповідь: і .

 

Самостійно розв’язати № 56 (11).

 

6. Метод потенціювання.

Розв’язати рівняння

 

.

 

Про потенціюємо дану рівність і отримаємо:

 

,

,

,

,

,

.

Перевірка:

Підставимо корінь .

,

,

.

Підставимо корінь .

,

.

Значення не є коренем рівняння, тому що вирази і не мають смислу.

Відповідь: .

 

Самостійно розв’язати № 53 (5).

 

Підсумок уроку.

 

Набули навичок і вмінь розв’язувати логарифмічні рівняння, що зводяться до квадратних відносно логарифмічної функції, з використанням переходу до іншої основи логарифмів, роздивилися методи логарифмування і потенціювання.

 

Д/З § 3 (розділ V),  № 52 (9, 11), № 53 (12), № 54 (7).

 

 

УРОК 5

 

Тема: Розв’язання логарифмічних рівнянь і систем рівнянь.

Мета: Формування умінь учнів розв’язувати системи логарифмічних рівнянь, логарифмічні рівняння різними методами.

Обладнання: таблиця основних властивостей логарифмів.

 

Хід уроку.

 

І. Повторення попереднього матеріалу.

1. На дошці, до початку уроку, записуються домашні завдання. Обговорюємо результати розв’язання рівнянь.

 

2. Самостійна робота.

 

І варіант.

Розв’язати рівняння:

1) ;
2) ;	а) і ;
3) ;	б) ;
4);	в) і ;
5) ;	г) і .
6).

 

ІІ варіант.

Розв’язати рівняння:

1) ;
2) ;	а) ;
3) ;	б) ;
4) ;	в) і ;
5) ;	г) і .
6) .

 

ІІ. Розв’язання систем логарифмічних рівнянь.

При розв’язанні систем логарифмічних рівнянь використовують ті самі способи, що й при розв’язанні алгебраїчних систем рівнянь – це спосіб підстановки і алгебраїчного додавання. Повторити з учнями ці способи розв’язування.

 

Наведемо приклади. Бажано викликати учня і, допомагаючи йому, розв’язувати.

 

1)

2)

 

Після розв’язання цих рівнянь, клас поділити на групи. Кожна група отримує своє завдання, а потім групи обмінюються завданнями. Після розв’язання завдань обговорюють відповіді, пояснюють не розв’язані системи.

І група № 56 (1)     ІІ група № 57 (1)

 

Колективне розв’язання систем показникових і логарифмічних рівнянь.

 

,

 

,

 

,

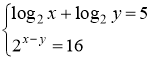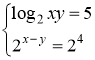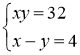далі система розв’язується система способом підстановки.

 

Підсумок уроку.

 

Набули навичок і вмінь розв’язувати комбіновані системи рівнянь, повторили розв’язання основних типів рівнянь та їх систем.

 

Д/З § 3 (розділ V),  № 55 (1, 2), № 56 (3), № 57 (2). Повторити властивості логарифмічної функції.

 

На дошці вивісити умови домашньої контрольної роботи.

 

 

 

ДОМАШНЯ КОНТРОЛЬНА РОБОТА

 

Розв’язати рівняння.

 

1) .

 

2) .

 

3) .

 

4) .

 

5) .

 

6) .

 

7) .

 

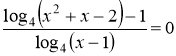8) .

 

9) .

 

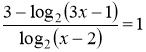10) .

 

11) При яких значеннях параметра рівняння має один корінь?