Урок "Розв’язування задач на застосування теореми Піфагора"
Геометрія, 8 клас
Тема. Розв’язування задач на застосування теореми Піфагора.
Мета уроку: узагальнити та систематизувати знання учнів про теорему Піфагора, формувати ключові компетентності, вміння розв’язувати задачі на застосування теореми Піфагора, розвивати увагу, логічне мислення, виховувати працьовитість, цікавість до математики, сприяти усвідомленню значення математики для повноцінного життя в сучасному суспільстві Тип уроку: комбінований.
Форма уроку: урок-гра.
Наочність та обладнання: портрет Піфагора,картки для учнів.
Хід уроку
Світ, що нас оточує, - це світ геометрії. Т Тож давайте його пізнавати!
І. Організаційна частина
Сьогодні у нас з вами незвичайний урок, але мені хочеться знати, які асоціації у вас викликає слово «урок»? Давайте розкладемо його по літерах.
У – успіх, Р – радість, О – обдарованість, К – кмітливість. І я сподіваюсь, що сьогодні на уроці на нас чекає і успіх, і радість, і ви зможете продемонструвати свою обдарованість і кмітливість. Ділю клас на 4 команди. Оголошення теми і мети уроку. Девізом уроку хай стануть слова: «Світ, що нас оточує, - це світ геометрії. Тож давайте його пізнавати!», який ми проведемо у формі гри (діти поділені на групи). Знайомтеся з капітанами груп: 1. …. , 2…..
ІІ. Перевірка домашнього завдання
1) розгадування кросворда
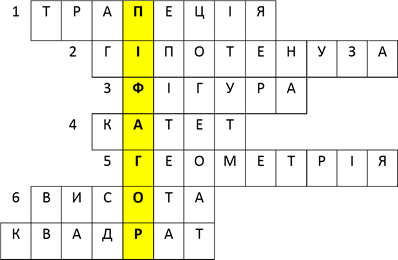1.Чотирикутник, у якогодвісторонипаралель
ні, а двіінші – не
паралельні . (Трапеція)
2.Найбільша ізсторінпрямокутноготри
кутника.(Гіпотенуза)
3.Трикутник – це ..., яка складаєтьсяізтрьохточок,
що не належать
7
однійпрямій, і трьохвідрізків, попарно з’єднуючихці точки. (Фігура)
4. Одна ізсторінтрикутника, щоутворюютьпрямий кут. (Катет)
5. Наука, яка вивчаєвластивостігеометричнихфігур. (Геометрія) 6. Перпендикуляр, проведений ізвершинитрикутника на протилежну сторону.(Висота)
7.Прямокутник, у якоговсісторонирівні. (Квадрат)
2) Запитання команд один одному: задати по два питання своїм противникам.
3) Історична довідка
Учень1.А визнаєте, щоолімпійськіігривперше почали проводитись у СтародавнійГреціїще до нашоїери. Змагання проводились з бігу на колісницях, кулачного бою. Цьогоміцного юнака з товстоюшиєю та коротким носом, справжньогозабіяку, суддіолімпіади не хотілидопускати до змагань, тому щовінбувдоситьмалий на зріст. Казали, що в нього «нізросту, нісили, нізовнішності». «Так, - сказав на цехлопець, - але я буду наноситиудари з математичноюточністю!» Йомувдалосяпобитисязісвоїми супротивниками, при цьомуще й перемогти. Цим хлопцембувПіфагор, великий математик. А подіяцявідбувалася у 548 році до н.е. на 58 олімпійськихіграх.
Учень 2. Піфагор народився близько 580 р. до н.е. на острові Самос. Там у сім'ї “золотих діл майстра” народився син. За давньою легендою, молодому подружжю Мнесахера і Парфеніси оракул устами бога АполонаПіфійського пророчив народження сина, який прославиться у віках своєю мудрістю, ділами і красою. Тому, коли народився син, йому дали ім'я Піфагор, тобто передбачений Піфієм.
Піфагор і справді виявив неабиякі здібності до наук. У свого першого вчителя Гермодамаса він вивчив основи музики і живопису. Зовсім юним він залишив батьківщину і вирушив до Єгипту. Але до Єгипту ще далеко і він на острові Лесбос у своїх родичів під опікою Фалеса кілька років навчався астрології, передбаченню затемнень, таємниці чисел, медицині. Піфагор відвідав також Вавілон, де він вивчив теорію чисел. Всі ці подорожі сприяли тому, що Піфагор став найосвіченішою людиною свого часу. В 60 років Піфагор повертається на свою батьківщину, де організовує школу, яка діяла майже 30 років.
Школа Піфагора – це заклад зі строго обмеженою кількістю учнів з аристократії і потрапити туди було дуже нелегко. Претендент мав витримати кілька іспитів. Піфагорійці прокидалися зі світанком, співали, акомпануючи собі на мрії, потім робили гімнастику, вивчали теорію музики, філософії, математики, астрономію та інші науки.
Основна ідея Піфагорійців “Початком усього є числа”. Без них нічого б не було і не було б порядку, гармонії. Піфагорійці приписували числам різні властивості. Парні числа вважалися нещасливими, а непарні – щасливими. Так, вважається, що слід дарувати букет з непарної кількості квіток. Піфагорійці розбили всі числа на непарні – “чоловічі”, і парні “жіночі”.
Прямокутний трикутник зі сторонами 3, 4, 5 називають Піфагоровим.
Піфагорових трикутників безліч (5; 12; 13), (6; 8; 10), (8; 15; 17), (7; 24; 25) і т.д.
Застосування теореми Піфагора різноманітне:
• для вимірювальних робіт (це знали ще в III тис. до н.е.);
• для геометричного знаходження квадратних коренів з цілих чисел;
• для знаходження степенів цілих чисел тощо.
Те, що Піфагор пов'язав реальний світ з числовими закономірностями, дало змогу більш пізнім поколінням учених зрозуміти краще світ і глибше.
ІІІ. Повідомлення теми, мети та завдань уроку
Отже, з інформаційних повідомлень ви зрозуміли, що сьогодні ми продовжуємопрацювати над темою «Розв’язування задач на застосування теореми Піфагора».
ІV. Актуалізація опорних знань
Продовжимо урок вправою «Гра у слова».
1) Створити ланцюжок слів, пов’язаних з математикою (Команди по черзі називають математичні терміни на букви а, б, в, г, к, п).
2) У майбутньому вам доведеться здавати ЗНО. Тому наступне завдання буде для вас таке.
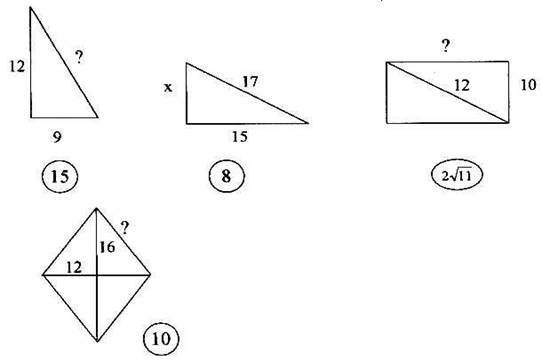
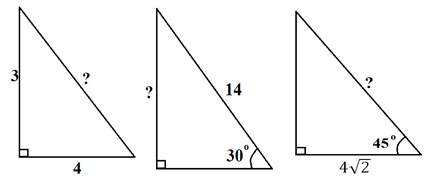
3) Бліцопитування«Аукціон знань» Який трикутник називається прямокутним?
• Як називаються сторони прямокутного трикутника?
• Яку сторону називають гіпотенузою?
• Які сторони називаються катетами?
• Чому дорівнює сума гострих кутів прямокутного трикутника? Чи може в прямокутному трикутнику бути два прямих кути? Чому?
• Перпендикуляр,проведений з вершини трикутника на протилежну сторону або її продовження…
• Закінчити речення: відрізок, що сполучає основу перпендикуляра з основою похилої…
• Як читається теорема Піфагора?
• Які проекції мають рівні похилі?
Учитель. Ми повторили деякі теоретичні питання курсу геометрії. Але знати математику – це не лише знати теоретичні відомості з тієї чи іншої теми, а і вміти їх застосовувати при доведенні теорем, розв’язуванні задач та вправ. Використовуючи той факт, що квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів катетів, можна довести багато інших теорем і розв’язати чимало різних задач.
V. Розв’язування задач та вправ
Кожна команда витягує картку з однією задачею і готує її розв’зок на дошці або на аркушах.
Дано: АВСD- рівнобічна трапеція АВ=4 см, ВС=5см, AD=11 см.
Знайти: ВК.
Розв’язання:
1) AK 
(ADBC) 
(115) 3(см)
2)З AKB, BK AB2 AK2 42 32 169 7
Завдання команді 2.
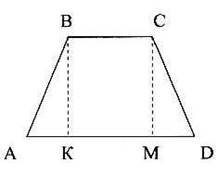Дано: АВСD- рівнобічна трапеція BC=7 см, ВK=4см, AD=13 см.
Знайти: AB.
Розв’язання:
Відповідь:
Завдання для обох команд
Дано прямокутну трапецію, у якої бічні сторони дорівнюють 17 дм і 15 дм, а менша основа – 9 дм. Знайти середню лінію трапеції.
Розв’язування задач з минулого. Старовинна задача. «Зламаний бамбук»
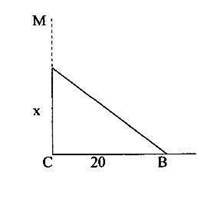Бамбук, що має 40 ліктів у висоту, було зламано вітром. Його верхівка торкнулася землі за 20 ліктів від основи стовбура. Скажи, о мудрий математик, на якій відстані від землі було зламано бамбук? Дано: МС=40 СВ=20.
Знайти: АС
Розв’язання:
МА=АВ
АС+АВ=40; АС=х; АВ=40-х
AB2 AC2 BC2- за т. Піфагора
AC2 AB2 BC2 x2 (40x)2 202
x2 402 80xx2 202
Лікоть- довжина від
ліктя до кінця 2
80x40 202
середнього пальця.
80x2060 4x60 x15
Відповідь: 15 ліктів. Задача
У народі кажуть «Без верби і калини нема України». Здавна в нашій місцевості на обійстях садили ці рослинисимволи. Знайдіть висоту верби, якщо довжина тіні, яку відкидає це дерево, дорівнює 4 м, а відстань від вершини стовбура до кінця тіні – 5 м. Відповідь: 3 м.
А зараз ми перевіримо ваше творчез авдання скласти сенкан зі слів «Теорема» або «Піфагор».
VІ. Домашнє завдання
_____________________
_____________________
VІІ. Підведення підсумків уроку. Рефлексія
Вправа «Рефлексивний екран» Висловіть свою думку про урок, вибираючи початок фрази з рефлексивного екрану на дошці. Учні по бажанню висловлюються одним реченням.
Виставлення оцінок
Вчитель. Щойно ви подолали певний рубіж, навчилися застосовувати теорему Піфагора: просту, красиву і значну до розв’язування задач.
Хотілося закінчити урок, згадавши вчення Піфагора, адже воно так нам необхідне в житті. Піфагор був не лише великим математиком, а й філософом. І я вважаю, що з даних висловів і ви зможете щось почерпнути для себе.
• Твори велике, не обіцяючи великого
• Нічому не дивуйся
• Тимчасова невдача краща від тимчасової удачі
• Живи з людьми так, щоб твої друзі не стали недругами, а недруги стали друзями
• Не роби нічого ганебного ні в присутності інших, ні таємно. Першим твоїм законом повинна бути повага до самого себе
• Лише неблагородна людина здатна в очі хвалити, а поза очі злословити
• Усе в світі підкоряється числам
• Роби лиш те, що в майбутньому не засмутить тебе
1. Чотирикутник, у якого дві сторони паралельні, а дві інші – не паралельні
2. Найбільша із сторін прямокутного трикутника
3. Трикутник – це ..., яка складається із трьох точок, що не належать одній прямій, і трьох відрізків, попарно з’єднуючих ці точки
4. Одна із сторін трикутника, що утворюють прямий кут
5. Наука, яка вивчає властивості геометричних фігур
6. Перпендикуляр, проведений із вершини трикутника на протилежну сторону
7. Прямокутник, у якого всі сторони рівні…
7
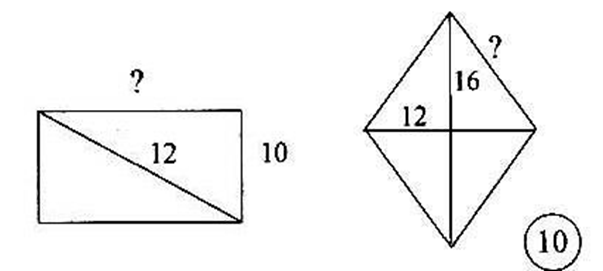
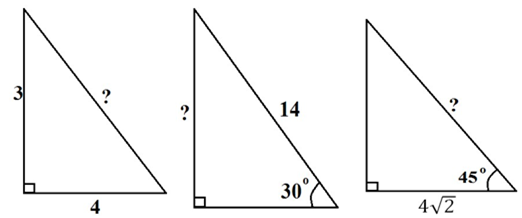
Задача 1.
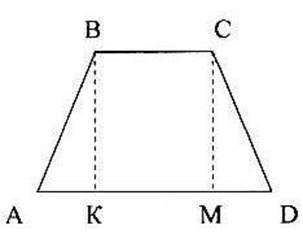Дано: АВСD- рівнобічна трапеція
АВ=4 см, ВС=5см, AD=11 см.
Знайти: ВК.
Задача 1.
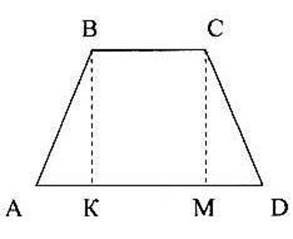Дано: АВСD- рівнобічна трапеція BC=7 см, ВK=4см, AD=13 см.
Знайти: AB.
Розв’язання:
Задача 2. Дано прямокутну трапецію, у якої бічні сторони дорівнюють 17 дм і 15 дм, а менша основа – 9 дм. Знайти середню лінію трапеції.
Задача 2. Дано прямокутну трапецію, у якої бічні сторони дорівнюють 17 дм і 15 дм, а менша основа – 9 дм. Знайти середню лінію трапеції.
Задача 2. Дано прямокутну трапецію, у якої бічні сторони дорівнюють 17 дм і 15 дм, а менша основа – 9 дм. Знайти середню лінію трапеції.
Задача 2. Дано прямокутну трапецію, у якої бічні сторони дорівнюють 17 дм і 15 дм, а менша основа – 9 дм. Знайти середню лінію трапеції.
Старовинна задача. «Зламаний бамбук»
Бамбук, що має 40 ліктів у висоту, було зламано вітром. Його верхівка торкнулася землі за 20 ліктів від основи стовбура. Скажи, о мудрий математик, на якій відстані від землі було зламано бамбук?
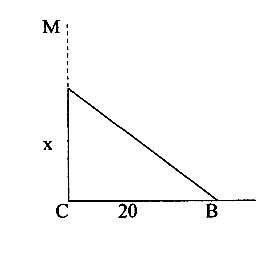Дано: МС=40, СВ=20.
Знайти: АС.
Розв’язання:
Лікоть- довжина від ліктя до кінця середнього пальця.
Старовинна задача. «Зламаний бамбук»
Бамбук, що має 40 ліктів у висоту, було зламано вітром. Його верхівка торкнулася землі за 20 ліктів від основи стовбура. Скажи, о мудрий математик, на якій відстані від землі було зламано бамбук?
Дано: МС=40, СВ=20.
Знайти: АС.
Розв’язання:
Лікоть- довжина від ліктя до кінця середнього пальця.
Задача
У народі кажуть «Без верби і калини нема України». Здавна в нашій місцевості на обійстях садили ці рослини-символи. Знайдіть висоту верби, якщо довжина тіні, яку відкидає це дерево, дорівнює 5 м, а відстань від стовбура до кінця тіні – 4 м.
Задача
У народі кажуть «Без верби і калини нема України». Здавна в нашій місцевості на обійстях садили ці рослини-символи. Знайдіть висоту верби, якщо довжина тіні, яку відкидає це дерево, дорівнює 5 м, а відстань від стовбура до кінця тіні – 4 м.
Задача
У народі кажуть «Без верби і калини нема України». Здавна в нашій місцевості на обійстях садили ці рослини-символи. Знайдіть висоту верби, якщо довжина тіні, яку відкидає це дерево, дорівнює 5 м, а відстань від стовбура до кінця тіні – 4 м.
про публікацію авторської розробки
Додати розробку