Урок "Розв'язування задач по темі: "Площі паралелограма, трикутника, трапеції"."
Тема уроку: Розв’язування задач по темі : «Площі паралелограма, трикутника, трапеції».
Мета уроку: Узагальнити і систематизувати знання учнів, вдосконалювати вміння і навички знаходити площі паралелограма, трапеції і трикутника; застосовувати здобуті знання на практиці, аналізувати результати, робити відповідні узагальнення, порівняння, висновки; розвивати пам’ять, логічне та дивергентне мислення; виховувати інтерес до математики, увагу, самостійність; формувати вміння працювати, вміння висловлювати свою думку.
Тип уроку: Узагальнення і систематизації;
Форма роботи: колективна; індивідуальна; парна.
Очікувані результати: Вміння використовувати формули для обчислення площ паралелограма, трикутника, трапеції на продуктивно-операційному рівні.
Основні завдання:
- Знати: формули для обчислення площ паралелограма, трикутника, трапеції;
- Вміти: застосовувати їх для розв’язування прикладних задач.
|
№ п/п |
Етапи уроку |
Час |
Методи і прийоми |
|
І |
Організаційний етап |
2 хвилини |
Прийом « рамки» |
|
ІІ |
Актуалізація опорних знань і умінь учнів |
5 хвилин |
Інтелектуальна розминка |
|
ІІІ |
Узагальнення вмінь і навичок учнів з теми через розв’язування задач |
10 хвилин |
«Здивуй!» |
|
ІV
|
Задачі за готовими малюнками |
8 хвилин |
Практичність теорії |
|
V |
Диференційовані завдання |
15 хвилин |
Робота в парах |
|
VI |
Рефлексія. Підсумок уроку |
3-5 хвилин |
«Напиши», прийом «рамки» |
Хід уроку:
I. Організаційний момент
Девіз уроку: Думаємо колективно,
Працюємо оперативно,
Сперечаємося доказово,
Це для всіх обов’язково.
Навчання мистецтву розв’язувати задачі – це виховання волі. (Д.Пойа)
- Актуалізація опорних знань і умінь учнів
- Сформулювати властивості (аксіоми) площ.
- Записати всі відомі формули для обчислення площ фігур.
- Які одиниці вимірювання площ ви знаєте?
-
Знайти зайву фігуру:
1. 2. 3.
(2.- присутня фігура, яка не є чотирикутником.)
5) Виключити зайвий рисунок:
а. б. в. г. д. е.
(д – фігура, які мають різні площі)
-
Виключити зайвий запис:
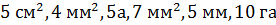(5мм)
- Серед запропонованих фігур знайти ті, які мають однакову площу.
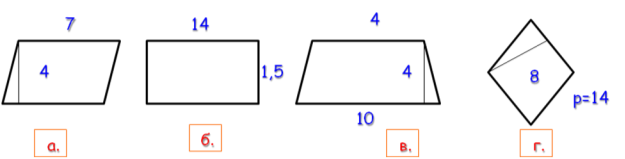
(однакову площу мають фігури 1, 3, 4)
ІІІ. Узагальнення вмінь та навичок учнів з теми через розв’язування задач.
Вміння розв’язувати математичні задачі часто полегшує життя, а іноді й зберігає його.
В оповіданні Л. Толстого «Чи багато людині землі потрібно» розповідається про селянина Пахома, який мріяв про власну землю.
Завдання, яке поставив Пахому старшина, полягало в тому, що Пахом отримає стільки землі, скільки обійде, але до заходу сонця він має повернутися в початкове положення. Та не судилося господарювати на цій землі Пахому, він помер . А якби знав математику, то можливо і залишився б господарювати. Давайте ми прослідкуємо шлях Пахома і з’ясуємо чи правильно він вибрав свій маршрут.
Шлях Пахома
Завдання І.
- Обчисліть площу ділянки землі і периметр:
А якби 40 верст Пахом пройшов би по сторонах квадрата, яку площу він би обійшов?
а = 10 верст, S = 100 (кв. верст)
Завдання ІІ.
Розгляньте таблицю і зробіть висновок:
|
Периметр
|
Р |
40 |
|||||
|
Сторона прямокутника
|
а
|
10 |
8 |
6 |
4 |
2 |
1 |
|
b
|
10 |
12 |
14 |
16 |
18 |
19 |
|
|
Площа
|
S |
100 |
96 |
84 |
64 |
36 |
19 |
Якщо периметр прямокутника сталий, тоді з усіх прямокутників з цим периметром найбільшу площу має квадрат.
Якби Пахом знав цю властивість, він міг би пройти, наприклад, усього 36 верст і в результаті обійти ділянку більшої площі.
Р = 94=36 (верст) S = 99=81 (кв. верст)
Тоді оповідання не мало б такого трагічного кінця:
- верста 1066,8 м.
IV. Задачі за готовими малюнками.
- Знайти площу ромбоподібної клумби, якщо відстань між протилежними її вершинами дорівнюють відповідно 5м і 8м.
-
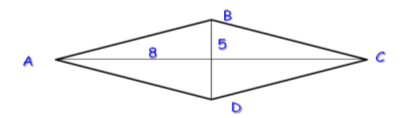
Площа залу
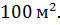Зал має форму паралелограма зі стороною 20 м. Знайти висоту цього паралелограма.
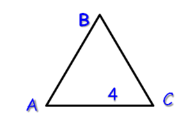
- Зал має форму правильного трикутника зі стороною 4м. Знайти площу підлоги.
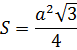
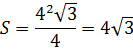
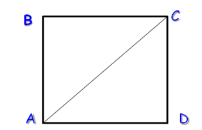
- Квадратна кімната по діагоналі 6м. Скільки квадратних метрів килимового покриття необхідно для покриття підлоги.
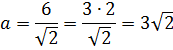
V. Диференційовані завдання:
Задача 1. Основою постаменту пам’ятника є квадрат зі стороною 6м. Навколо пам’ятника проходить алея шириною 2м. Знайти площу алеї.
Освітлення кімнати вважається нормальним, якщо площа вікон складає не менше 0,2 площі підлоги. Визначити, чи є нормальним освітлення нашої класної кімнати.
2*2м
Ширина: 6,2 м, довжина: 8м.
; 
Уже при площі вікон 10
освітлення кімнати є нормальним.
Пофарбована стіна довжиною 8,25м і висотою 4,32м має три вікна розміром 2,2*1,2 м*м кожне. Знайти площу тієї поверхні стіни, яка пофарбована.
Задача 4. Ставок має форму квадрата. У вершинах квадрата на березі ставка ростуть чотири дуба. Хочуть вдвічі збільшити площу ставка, але так, щоб всі чотири дуба залишалися цілими (тобто були на березі). Як це зробити?
B C
A D
Побудуємо точки О1,О2,О3,О4, симетричні точці О відносно прямих BC, AD, CD, і AB відповідно. Доведемо, що площа утвореного квадрата вдвічі більша за площу початкового.
VI. Підсумок уроку. Рефлексія, Оцінювання.
- Що ми сьогодні робили на уроці?
- Для чого нам потрібні ці знання?
- Який з чотирикутників із сталим периметром має найбільшу площу?
На заздалегідь заготовлених аркушах паперу діти пишуть речення, починаючи зі слів: Я знаю… Я вмію…. Я можу… , прикріплюють на плакат.
Оцінюємо рівень навчальної компетентності учнів:
- За роботу на всіх етапах уроку
- За роботу на окремих етапах уроку.
Домашнє завдання:А.П.Єршова, В.В.Голобородько : повторити §18, ст.. 193 задачі 1-5
Пам’ятайте: «Тисячі шляхів ведуть до помилки, до істини тільки один»
то ж я вам бажаю, щоб ви завжди вибирали той єдиний правильний шлях до істини, і допоможуть вам в цьому ваші знання геометрії.
Діти, я вдячна вам за роботу, а гостям я вдячна за увагу. Допобачення.
Використана література:
- С.С.Варданян. Задачи по планиметрии с практическим содержанием: Кн.для учащихся 6-8 кл. сред.шк. / Под ред.. В.А.Гусева – М.: Просвещение, 1989. – 144с.
-
А.П.Єршова, В.В.Голобородько Підручник з геометрії для учнів 8 класу.
про публікацію авторської розробки
Додати розробку