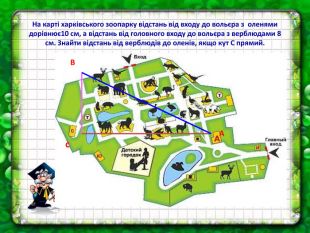
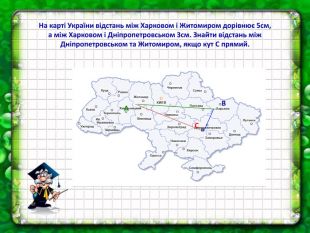
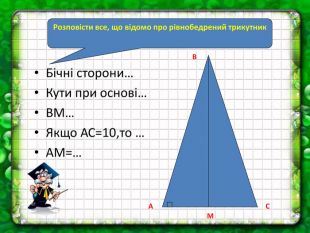
Урок розв'язування задач "Теорема Піфагора"
Про матеріал
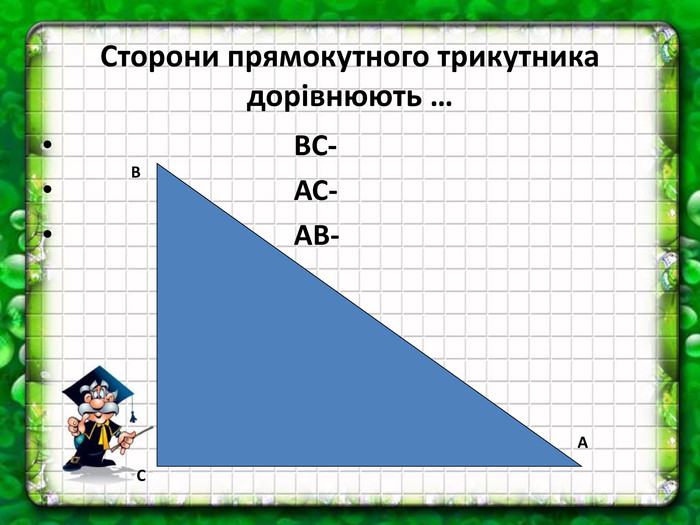
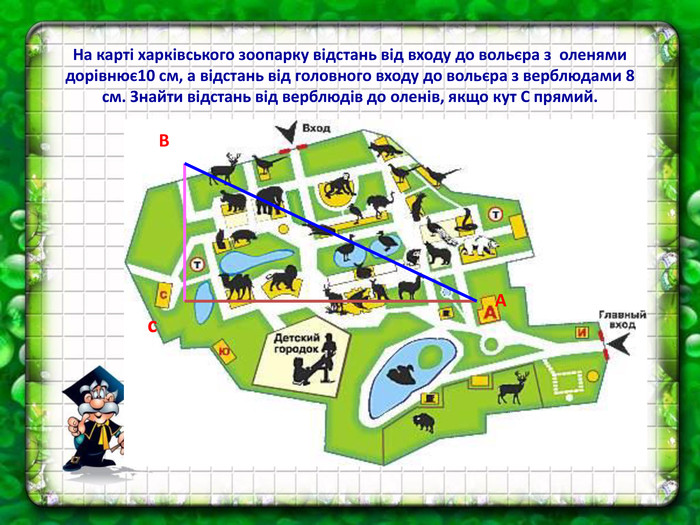
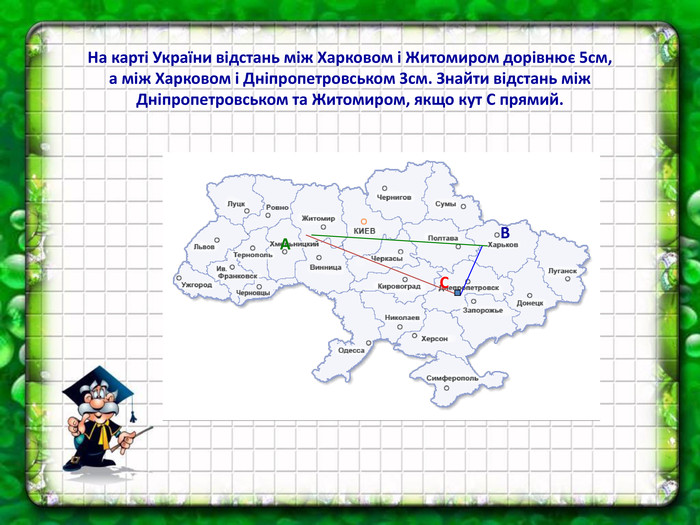
Теорема Піфагора - одна з найважливіших теорем у геометрії. Чим цікавішим буде урок, тим більше шансів отримати кращий результат по засвоєнню теореми та її формули. У презентації до уроку використовуються задачі практичного змісту із навколишнього життя. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дякую! Із задоволенням використаю на своїх уроках!
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку