Урок "Середні величини"
Средние величины
(урок-семинар для учащихся 9 классов)
Яворская Ирина Степановна,
учитель математики Криворожской
специализированной школы
І-ІІІ уровней №71
В ходе семинара учащиеся должны повторить материал по темам «Подобие фигур», «Площади фигур», «Среднее арифметическое двух чисел», «Среднее геометрическое двух чисел», а также усвоить новые понятия, такие как среднее квадратичное и среднее гармоническое двух чисел. Во второй части семинара предусмотрено выполнение практической работы по построению отрезков окружности, имеющих длины, равные средним величинам данных двух отрезков.
Тема урока. Средние величины
Цели урока. Повторить материал о средних величинах, изученных ранее: среднее арифметическое и среднее геометрическое. Ввести понятие среднего гармонического и среднего квадратичного величин. Закрепить понятия в процессе решения задач и выполнения практической работы.
Тип урока. Совершенствование знаний, умений, навыков.
Форма урока. Семинар (2 урока)
Оборудование. Мультимедийный проектор, переносная доска, компьютер, рисунок трапеции, цветные плоски.
Ход урока.
І.Актуализация знаний учащихся.
Когда говорят «средний возраст», «средний рост», «средний заработок», всем понятно, о чём идёт речь. В математике рассматривается множество различных «средних» величин, поэтому всегда нужно уточнять, какое именно «среднее» имеют в виду.
В самом общем смысле среднее значение нескольких чисел – это некоторое число, заключённое между наименьшим и наибольшим из них.
Вопросы учащимся.
- С какими средними величинами вы знакомы?
- Как найти среднее арифметическое двух чисел, нескольких чисел?
- Как найти среднее геометрическое двух чисел?
- Где в алгебре и геометрии вы встречались с этими понятиями?
Учащиеся на доске записывают формулы n-ого члена арифметической и геометрической прогрессий через среднее арифметическое и среднее геометрическое членов пропорции и выражают отрезки в прямоугольном треугольнике как среднее геометрическое двух других.
ІІ. Изучение новых понятий.
Учитель знакомит учащихся со средним гармоническим и средним квадратичным. Записывают определения. После этого необходимо записать формулы для нахождения средних величин для двух чисел, отличных от нуля.
Среднее арифметическое: m = ![]()
Среднее геометрическое:![]() g =
g =![]() ,
, ![]() > 0
> 0
Среднее гармоническое: h = 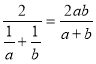
Среднее квадратичное: ![]()
Арифметическое, геометрическое и гармоническое средние значения были известны ещё античным математикам. Эти средние связаны с теорией пропорций, которая лежала в основе древнегреческого учения о музыке, геометрической теории чисел, а позже – теории площадей.
ІІІ. Совершенствование знаний, умений, навыков.
А как располагаются эти величины в порядке возрастания? Чтобы ответить на этот вопрос, нужно выполнить задание.
Задание
Расположить числа m, g, h, S в порядке возрастания.
І вариант. a=3, b=9
(m=6, g=![]() , h=4,5, S=
, h=4,5, S=![]() ;
; ![]() )
)
ІІ вариант. a=5, b=7
(m=6, g=![]() , h=
, h=![]() , S=
, S=![]() ;
; ![]() )
)
Вывод
![]()
![]()
Вопрос. Когда между величинами можно поставить знак равенства?
(когда a=b)
Решение задач
Для решения задач класс делится на 4 группы. После выполнения работы к доске выходят по одному человеку из каждой группы для записи решения. На доске заранее заготовлены рисунки. Цветным мелом чертят отрезки.
|
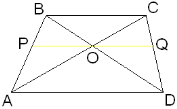
Задача 1
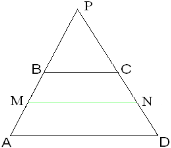
Дано: АВСD –трапеция ВС=b, AD=a, AC∩BD=O, OєPQ, PQ||AD Найти: PQ Решение 1) ∆APO ~ ∆ABC (по двум углам)
2) ∆PBO ~ ∆ABD
3) Сложим почленно (1) и (2)
4) Аналогично
5)
Среднее гармоническое.
|
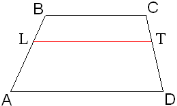
Задача 2
Дано: ABCD-трапеция, BC=b, AD=a, ALTD~LBCT Haйти: LT Решение
Так как ALTD и LBCT подобны, то
Среднее геометрическое.
|
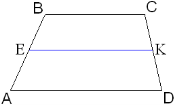
Задача 3
Дано: ABCD-трапеция, BC=b, AC=a, E-середина AB, K-середина CD Найти: EK Решение EK-средняя линия трапеции
Среднее арифметическое |
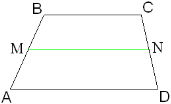
Задача 4
Дано: ABCD-трапеция, BC=b, AD=a,
Найти: MN Решение 1)Достроим трапецию до треугольника
2)∆BPC~∆MPN, S1-площадь ∆BPC S-площадь МВСN или AMND Пусть MN=x, тогда
3)∆APD~∆MPN
4)Почленно сложим (1) и (2)
квадратичное
|
Обобщим полученные результаты. На переносной доске выполнен рисунок, к котрому учащиеся прикрепляют бумажные полоски.
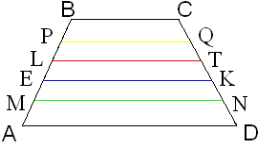
Практическая работа
В античной математике, по преимуществу геометрической, большое внимание уделялось построениям с помощью циркуля и линейки. Было принято несколько способов построения средних по двум данным отрезкам a и b. В „Математическом собрании” Папа Александрийского (III в.) – своде достижений древнегреческой математики – приведены различные построения средних значений по методам его предшественников, дано также описание построения трех средних на одной фигуре.
Задание классу
1) Отложите на прямой a смежные отрезки AM=a и MB=b. На отрезке AB как на диаметре постройте окружность с центром О. Чему равен радиус этой окружности? (Выразите R через a и b)
![]() - среднее арифметическое
- среднее арифметическое
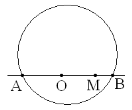
2) Проведите перпендикуляр CM, C лежит на окружности. Найдите CM через a и b. Указание. Рассмотрите ∆ОСМ.
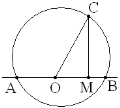
![]()
![]()
![]()
![]() =>
=>
![]() - среднее геометрическое
- среднее геометрическое
3) Проведите высоту MN треугольника OMC. Найдите CN через a и b.
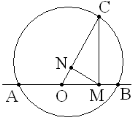
∆CMN~∆COM
![]() =>
=> ![]()
![]() - среднее гармоническое
- среднее гармоническое
4) Проведите перпендикуляр ОD к прямой а. (Точки С и D для удобства расположите по разные стороны от АВ на окружности). Найдите DМ через а и b.
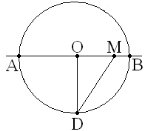
∆OCM:
![]() ;
;
![]()
![]() - среднее квадратичное.
- среднее квадратичное.
IV. Домашнее задание.
Подготовить сообщение о взвешенных средних величинах.


про публікацію авторської розробки
Додати розробку