Контрольна робота на тему "Геометричні переміщення".
___________________________________________________________________________________________________
9 клас КР № 5 Геометричні переміщення Варіант І
-
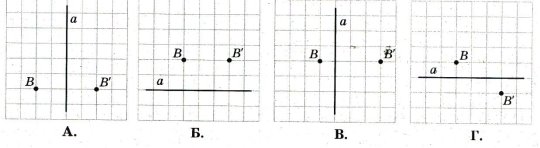
Укажіть малюнок, на якому точки
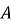 і
і  симетричні відносно прямої
симетричні відносно прямої  .
.
- Укажіть неправильне твердження.
А. Прямі, на яких лежать діагоналі ромба, є його осями симетрії.
Б. Існує поворот, унаслідок якого одна з основ трапеції переходить в іншу.
В. Центр кола є центром його симетрії.
Г. Унаслідок переміщення будь-яка фігура переходить у рівну їй фігуру.
-
Паралельне перенесення задано формулами
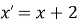 ,
, 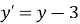 . У яку точку при такому паралельному перенесенні перейде точка
. У яку точку при такому паралельному перенесенні перейде точка 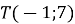 ?
?
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
При переміщені трикутник
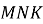 перейшов у трикутник
перейшов у трикутник 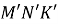 . Знайдіть кути трикутника
. Знайдіть кути трикутника 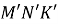 , якщо трикутник
, якщо трикутник 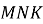 є рівнобедреним з основою
є рівнобедреним з основою 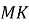 і
і 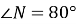 .
.
-
Точки
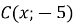 і
і 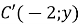 симетричні відносно точки
симетричні відносно точки 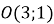 . Знайдіть
. Знайдіть 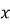 і
і 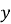 .
.
-
Унаслідок повороту навколо початку координат на
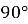 проти годинникової стрілки центр кола, заданого рівнянням
проти годинникової стрілки центр кола, заданого рівнянням 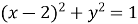 ,переходить у деяку точку А. Знайдіть координати цієї точки.
,переходить у деяку точку А. Знайдіть координати цієї точки.
-
Складіть рівняння кола, симетричного колу
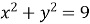 відносно точки з координатами
відносно точки з координатами
- (2;0) ; 2) (0;5);
-
Задайте формулами паралельне перенесення, унаслідок якого середина відрізка AB переходить у середину відрізка CD, якщо:
- A(2;8), B(8;2), C(4;11), D(10;9);
- A(-7;-3), B(-1;-5), C(2;6), D(10;8);
-
Запишіть рівняння прямої, що симетрична прямій
 відносно початку координат.
відносно початку координат.
___________________________________________________________________________________________________
___________________________________________________________________________________________________
9 клас КР № 5 Геометричні переміщення Варіант ІІ
-
Укажіть малюнок, на якому точки
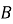 і
і 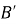 симетричні відносно прямої
симетричні відносно прямої 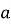 .
.
- Укажіть неправильне твердження.
А. Точка перетину паралелограма є його центром симетрії.
Б. Пряма, яка містить бісектрису кута є віссю його симетрії.
В. Існує паралельне перенесення, яке переводить один з двох вертикальних кутів в інший.
Г. Рівні фігури переводяться одна в одну переміщенням.
-
Паралельне перенесення задано формулами
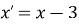 ,
, 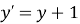 . У яку точку при такому паралельному перенесенні перейде точка
. У яку точку при такому паралельному перенесенні перейде точка 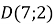 ?
?
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
При паралельному перенесенні трикутник
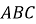 перейшов у трикутник
перейшов у трикутник 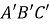 . Знайдіть кути трикутника
. Знайдіть кути трикутника 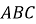 , якщо трикутник
, якщо трикутник 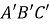 є рівнобедреним з основою
є рівнобедреним з основою 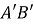 і
і 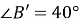 .
.
-
Точки
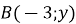 і
і 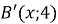 симетричні відносно точки
симетричні відносно точки 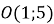 . Знайдіть
. Знайдіть 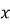 і
і 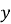 .
.
-
Унаслідок повороту навколо початку координат на
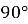 проти годинникової стрілки центр кола, заданого рівнянням
проти годинникової стрілки центр кола, заданого рівнянням 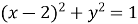 ,переходить у деяку точку А. Знайдіть координати цієї точки.
,переходить у деяку точку А. Знайдіть координати цієї точки.
-
Складіть рівняння кола, симетричного колу
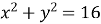 відносно точки з координатами
відносно точки з координатами
-
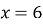 ; 2)
; 2) 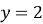
-
-
Задайте формулами паралельне перенесення, унаслідок якого середина відрізка AB переходить у середину відрізка CD, якщо:
- A(3;4), B(10;-2), C(7;7), D(9;-1);
- A(2;4), B(8;2), C(-4;3), D(-6;7);
-
Запишіть рівняння прямої, що симетрична прямій
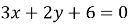 відносно початку координат.
відносно початку координат.
___________________________________________________________________________________________________
-
Дякую!
-


про публікацію авторської розробки
Додати розробку
