Урок "Середня лінія трапеції"

Тетяна Щербакова,

вчитель математики

Геометрія 8 клас

Тема. Середня лінія трапеції

Мета: Сформувати в учнів поняття середньої лінії трапеції; працювати над засвоєнням змісту теореми про властивість середньої лінії трапеції, а також схеми її доведення;

         формувати в учнів уміння відтворювати зміст вивчених на уроці   тверджень, розпізнавати на малюнку та виконувати зображення середньої лінії трапеції; формувати навички застосування вивченої властивості середньої лінії трапеції. 

розвивати пам’ять учнів, культуру математичного мовлення, спостережливість, уважність, інтелектуальні та творчі здібності;

сприяти реалізації наскрізної змістової лінії «Підприємливість і фінансова грамотність», яка пов´язана з розв´язанням практичних завдань, формулюванням власних пропозицій, умінням використовувати власний життєвий досвід, розвитком лідерських ініціатив.

           виховувати працьовитість, творчість, наполегливість у досягненні поставленої мети, вміння співпрацювати.

Тип уроку: засвоєння нових знань.

Наочність та обладнання: конспект «Середня лінія трапеції», моделі трапеції, трикутників, картки із завданнями.

Хід уроку

1.                Організаційний етап

   Організація учнів. Перевірка рівня готовності до уроку.

ІІІ. Формулювання мети і завдань уроку

Учитель повідомляє учням про те, що на уроці вони нарешті будуть вивчати ту властивість трапеції, заради якої було вивчено теорему Фалеса та поняття і властивості середньої лінії трикутника. Вивчення означення та властивості цього нового елемента трапеції, а також ово­лодіння способами використання вивчених на уроці тверджень під час розв'язування задач і є основною метою уроку.

Вправа «Гра слів»

Діти об’єднуються в коло обличчям один до одного.

   Погляньте одне на одного й подаруйте посмішку. Візьміться за руки, відчуйте дотик тепла товариша і побажайте йому всього найкращого.

Завдання. Створити ланцюжок слів, пов’язаних з математикою. Кожне наступне слово повинно починатися на передостанню букву попереднього.

IV. Актуалізація опорних знань

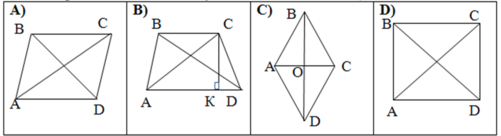
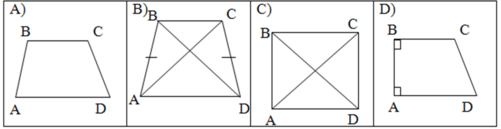
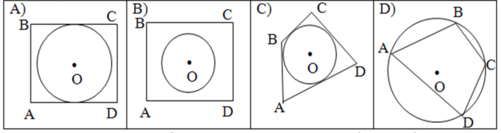
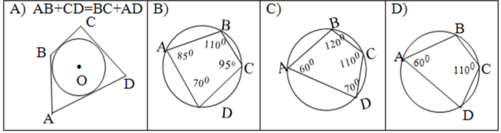
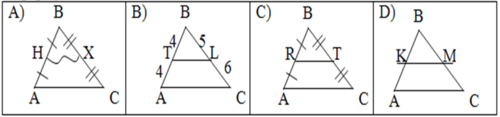
 1. Робота з готовими малюнками

1.                   На якому з малюнків зображено трапецію? Назвіть її елементи (основи, бічні сторони, діагоналі, висоту та дайте їх визначення).

2.                   На якому з малюнків зображено рівнобічну трапецію? Сформулюйте її властивості .

3.                   На якому з малюнків зображено описаний чотирикутник? Сформулюйте його визначення

4.                   На якому з малюнків продемонстровано властивість сторін описаного чотирикутника? Сформулюйте її.

5.                   На якому з малюнків зображено середню лінію трикутника? Сформулюйте її визначення

6.                   Скільки середніх ліній існує в трикутнику?

2. Робота в групах  Розв’язування практичних задач

1 група «Конструктори». Розрізати трикутник на 3 частини, кожна з яких матиме форму трапеції.

2 група «Охоронці». Фруктовий садок має форму трапеції, в якій основи відносяться, як 16:11, причому менша основа на 250 м менша за більшу, а бічні сторони 700 і 650 м. За скільки хвилин охоронець може обійти вздовж огорожі всю ділянку, якщо його швидкість 4м/хв.

3. Робота в парах

Встановити відповідність

VІ. Вивчення нового матеріалу

Запитання до учнів:

• Який відрізок можна назвати середньою лінією трапеції? Після відповіді учням пропонується в зошиті виконати рисунок трапеції і побудувати її середню лінію.

Після того, як ввели поняття середньої лінії трапеції, створюється проблемна ситуація:

Задача  У парку, який має форму  трапеції, відвідувачі полюбляють ходити  навпростець. Стежка сполучає середини бічних сторін трапеції.  Сторони парку, які виступають основами трапеції становлять 120м і 140м. Яка довжина стежини.

• Чи має середня лінія трапеції такі самі властивості, як і середня лінія трикутника?
• Виміряйте середню лінію трапеції і спробуйте встановити, яка залежність існує між ними.
• Учні пробують формулювати властивість середньої лінії, перевіряють практично.  

Формулюється теорема, в зошитах записується її умова і висновок.

  Проводиться доведення теореми:

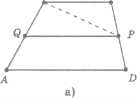
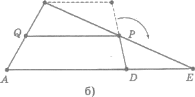
Ідею доведення теореми демонструється  на простій моделі. З цупкого аркуша картону вирізається трапеція АВСD (мал.1.а). На тра­пеції зображується середня лінія QР, а частина трапеції (трикутник ВСР) відрізається і шарнірно закріплюється в точці Р. Як тільки учні виконають додаткову побудову і зможуть відповісти на останнє запитання, цю частину розвертають на 180° утворюючи новий трикутник АВЕ(мал. 1.б.)

               Що треба довести, щоб відрізок РQ був середньою лінією цього трикут­ника? (РВ = РЕ)

• Як це довести? (Із рівності трикутників РВС і РЕD.)
• Які властивості середньої лінії трапеції випливають з властивостей

середньої лінії трикутника? ( РQ || АЕ і РQ = АЕ .)

• Чи буде середня лінія трапеції паралельна основі ВС?
• Виразити відрізок АЕ через основи трапеції.

Після доведення повертаємось до розв'язання проблемної ситуації

VII Закріплення вивченого матеріалу.

1.   Вказати середню лінію трапеції. Пояснити думку.(усно)

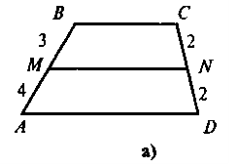
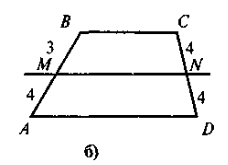
Виконання письмових вправ

№ 315(колективно),

№319 (з наступним коментуванням),

Весела перерва

Запрошуються 6 хлопчики добровольців, які отримують завдання утворити пари і кожна пара зображає  прямокутну трапецію, рівнобічну трапецію, довільну трапецію.

№ 326 (з висуненням гіпотези)

Додаткове завдання(за рахунок вільного часу, або для учнів, які вже виконали завдання). Конверти з прямокутними трикутниками і завданням роздаються учням.

ЦІКАВА ЗАДАЧА

Скласти трапецію з:

а) чотирьох прямокутних трикутників;

б) із трьох прямокутних трикутників;

в) із двох прямокутних трикутників.

VII. Підсумки уроку

Виконання інтерактивних вправ в сервісі

https://learningapps.org/8182846

У наведених твердженнях знайдіть та виправте помилки.

1.             Середня лінія трапеції сполучає середини двох сторін трапеції.
2.             Середня лінія сполучає середини основ трапеції.
3.             Середня лінія трапеції сполучає бічні сторони трапеції.
4.             Середня лінія трапеції дорівнює сумі основ.
5.             Середня лінія трапеції дорівнює півсумі сторін трапеції.
6.             Середня лінія трапеції паралельна до сторони трапеції.
7.             Середня лінія трапеції проходить через точку перетину діагоналей трапеції.

VIII. Завдання додому

Вивчити зміст означення, властивості та доведення властивості се­редньої лінії трапеції.

Розв'язати задачі.

Впр. 316, 319, 327.

«Творче завдання»

Скласти байку або казку до теми «Трапеція. Середня лінія трапеції»