Урок "Системи рівнянь другого степеня"

Тема: Системи рівнянь другого степеня

Мета:

• узагальнити і систематизувати знання учнів з теми «Системи рівнянь другого степеня»;
• закріпити вміння і навички учнів використовувати набуті під час вивчення теми знання для розв’язування вправ і задач, розвивати увагу учнів, логічне мислення, творчу активність;
• виховувати ввічливе ставлення до однокласників та учителя, культуру мовлення та культуру поведінки.

Тип уроку: контроль і корекція знань, умінь і навичок

Хід уроку

1.               Організаційний етап. Учитель налаштовує учнів на роботу.

Перевірка домашнього завдання.

Учні-консультанти проводять перевірку домашнього завдання на перерві.

2.               Формулювання теми, мети і завдань уроку.

На цьому уроці нашим завданням буде систематизувати та узагальнити  ваші вміння розв’язувати системи рівнянь другого степеня та задачі складанням систем рівнянь.

3.               Актуалізація опорних знань учнів.(слайд 1 - 18)

Як розв’язувати системи рівнянь другого степеня двома способами – повторимо за допомогою трьох аналітичних груп. У процесі повторення запишіть елементи схем у опорний конспект робочого зошита (групи представляють схеми розв’язування, висновки щодо переваг та недоліків того чи іншого методу) (проектні роботи у виді презентацій)

4.               Удосконалення вмінь і навичок учнів. (слайд 19, 20)

 Отже, основні алгоритми ми з вами повторили, а тепер перевіримо, наскільки якісно ви засвоїли вивчений матеріал.

1. Яка з наступних пар чисел є розв’язком системи рівнянь:

  А) (-6; 8) Б) (6; -8) В) (-6;8) Г) (6; 8)

2. На рисунку зображені графіки функції у = -х² – 2х + 3, у = х + 3 і

у = 1 – х.

Користуючись рисунком розв’язати систему

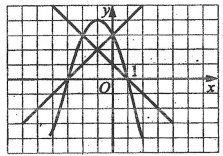
А) (0; 3), (-3, 0)  Б) (1; 0), (-2; 3)  В) (-1; 2)   Г) (1; 0), (-3; 0)

  3) Два учні розв’язують завдання біля дошки

 Розв’яжіть систему графічно і способом підстановки.

      Відповідь: (0; -3), (-3; 0)

  4) Математична естафета. Шановні учні. Ми з вами переконалися у своїх можливостях розв’язувати системи рівнянь різними способами. Ці навички є особливо важливими для уміння розв’язувати задачі. Отже, якщо ви вмітимете складати системи рівнянь до задачі, а навички їх розв’язань у вас є, то вважайте, що ви цілком впоралися із своїм сьогоднішнім завданням. Перед вами на слайді триколірний щит. Це символ світлофора – перепустки до тематичної атестації. Зараз кожна команда отримає набір із трьох задач (додаток 1). Вашим завданням буде записати на дошці математичну модель задач, тобто скласти до них системи. Робити це слід у естафетному порядку. Майте на увазі: перші задачі – середнього рівня, другі – достатнього рівня, треті – високого. Після закінчення естафети – перевірка правильності на слайді. Перші задачі -  зникає червоне світло. Другі – жовте, треті – зелене. Відкривається вислів Галілео Галілея, який є підсумком уроку. (слайд 21)

5.      Домашнє завдання: Повторити п.13, 14. Виконати вправи №145(3), 147(6), 158, вар.3 (слайд 22)
6.               Релаксація.  Учням роздані набори кольорових прямокутників (зеленого, жовтого та червоного кольору). Кожен обирає собі той колір, який в тій чи іншій мірі відображає рівень готовності до контрольної роботи (по принципу світлофора).
7.               Оцінювання  (мотивація балів та їх виставлення).

Додаток 1.

Група 1.

1. Сума двох чисел дорівнює 20, а їх добуток – 12. Знайдіть числа.
2. Периметр прямокутника 26 см, а його діагональ 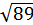см. Знайдіть сторони прямокутника.
3. Змішавши 10%-й та 30%-й розчини кислоти, отримали 600 г 20%-го розчину. Скільки грам кожного розчину слід було взяти?

Група 2.

1. Різниця двох чисел дорівнює 15, а їх добуток – 100. Знайдіть числа.
2. Периметр прямокутного трикутника 20 см, а його гіпотенуза 10 см. Знайдіть катети трикутника.
3. Маючи 45%-й та 60%-й сплави цинку, отримали 260 кг 50%-го сплаву. Скільки кілограмів кожного сплаву слід було взяти?

Група 3.

1. Сума двох чисел дорівнює 20, а їх частка – 3. Знайдіть числа.
2. Одна із сторін прямокутника на 8 см довша від іншої, а його діагональ 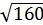см. Знайдіть сторони прямокутника.
3. У результаті змішування 70%-й та 90%-й розчинів спирту отримали 30 г 85%-го розчину. Скільки грамів кожного розчину слід було взяти?