Урок" Системи рівнянь з двома змінними"

Алгебра 9 клас урок – судове засідання.

Тема: Розв’язування систем рівнянь із застосуванням різних способів.

Мета: узагальнити способи розв’язування систем рівнянь, формувати вміння і навички         досліджувати і розв’язувати системи рівнянь;

           Розвивати пізнавальний інтерес, увагу, пам'ять ;

           Спонукати до творчої самостійної праці;

         Виховувати любов до предмета.

ХІД УРОКУ

І. Організаційний момент.

ІІ. Повідомлення теми і мети уроку.

Учитель. Сьогодні предметом дослідження  на уроці буде тема «Розв’язування систем рівнянь із застосуванням різних способів». Це питання надзвичайно важливе. Воно протягом трьох років розглядається в шкільному курсі математики.

Чому так багато часу відводиться для вивчення цієї теми?

Які задачі економіки, фізики зводяться до розв’язування систем рівнянь ?

Які способи їх розв’язання є раціональними?

Ці питання настільки важливі, що розібратися в них може лише судове засідання.

ІІІ. Судове засідання.

Секретар: Встати, суд іде.

Суддя:  Шановні юні математики! Сьогодні ми проводимо незвичайне судове засідання. Звинувачують ся різні способи розв’язувань. Що ж привело їх на лаву підсудних.

Прокурор: Пані та панове! Хочу повідомити вам, що з того часу, як учні почали вивчення  різних способів розв’язування систем рівнянь, між ними точаться чвари, суперечки, дискусії, який із способів кращий, раціональніший; якому способу надати перевагу.

       Цю суперечку потрібно негайно вирішити, бо не тільки розпадається колектив класу, а й відомі світові відкриття математики зазнають краху.

            А тому я вимагаю розібратися з питаннями, які виникли, і засудити з усією строгість закону способи розв’язування систем рівнянь, або оправдати їх.

Суддя: Розпочинаємо судове засідання. Кожен має право захисту, а також може ознайомитися із з доказами обвинувачення – це збірники задач і вправ, якими користуються учні. Щоб когось звинуватити и виправдати, як різні способи застосовують до розв’язування систем рівнянь . а тому  викликаю свідків – учнів класу.

Учитель: Шановні свідки, вам пропонується розв’язати системи рівнянь способами підстановки, додавання та порівняння.

Троє учнів розв’язують біля дошки, решта – в зошитах

підстановки

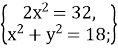додавання

порівняння

Учитель. З чого починаємо, коли розв’язуємо систему способом порівняння?

Учень. Спочатку виражаємо  в кожному рівнянні системи одну змінну через іншу.

Учитель. Яку змінну виражали в даному випадку?

Учень. Змінну х через у.

Учитель. Що робимо далі?

Учень. Порівнюємо знайдені для х вирази і одержуємо рівняння з однією змінною. Розв’язуємо його, знаходимо значення змінної у, а потім відповідне значення змінної х.

Учитель. Зверніть увагу на дошку, чи система розв’язана правильно?

Прокурор. Я вважаю, що спосіб додавання не є раціональним, бо якщо коефіцієнти при змінних великі, то потрібно затратити багато часу на виконання додаткових обчислень.

Адвокат. Панове, але для даної системи він є раціональним і крім того, при розв’язуванні задач на складання систем рівнянь, ми будемо користуватися цим способом доволі часто.

Прокурор. Спосіб порівняння я взагалі пропоную засудити і прошу Вашого дозволу викликати наступного свідка.

(Учень виходить до дошки і коментує запис розв’язання третьої системи методом Крамера)

Розв’язання = 8;

                                 ,

= = 1;           у =

Відповідь (1;1)

Прокурор. Як бачите методом Крамера, розв’язки знайти набагато простіше, ніж методом порівняння..

Адвокат. Шановне товариство! Я все таки хочу захистити спосіб порівняння. Що таке «визначник»?  якщо відкриємо словник математичних термінів, то побачимо, що в перекладі з латині це слово означає «обмежений». Справді, даний метод можна використовувати тільки для систем лінійних рівнянь. А способом підстановки, додавання і порівняння – і для систем, вищих степенів.

СУДДЯ. Слово надається підсудним.

Підсудний. Шановний суд! Ще в 1693 р. Лєйбніц писав: «Правило обчислення розв’язків лінійної системи за допомогою визначників, а також способи дослідження розв’язків залежно від них – одне з найкращих відкриттів у алгебрі».

Коли доведеться розв’язати систему рівнянь з параметрами, то метод Крамера – один із раціональних способів, без якого важко буде обійтися. Крім того, теорія визначників використовується в електротехніці.

Суддя. Викликається наступний свідок.

Учитель. Потрібно розв’язати систему рівнянь  способом підстановки з коментарем.

Прокурор. Спосіб підстановки можна використати і тоді, коли одне з рівнянь системи другого степеня. Думаю, що ним можна було б розв’язати всі попередні системи.

Суддя. А якщо дано систему рівнянь виду:

Можна використати спосіб підстановки чи ні ? викликаю наступного свідка.

Учень. Для розв’язування такої системи можна застосувати теорему, обернену до теореми Вієта. Можна стверджувати, що значення х і у, які задовольняють дану систему рівнянь є коренями квадратного рівняння, складеного за допомогою цієї теореми.

Учитель. Сформулюйте дану теорему.

 Учень формулює, учні аналізують розв’язки системи рівнянь, записаної на дошці.

Відповідь (4; 3), ( 3; 4).

Прокурор. Цей прийом зручний тільки для систем двох рівнянь з двома змінними, розв’язками яких є лише цілі числа.

Адвокат.  Заперечую , і прошу взяти до уваги факт, якщо ; - корені рівняння +то

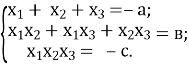
Суддя. Слово надається підсудним.

Учень я хочу розповісти про батька алгебри Франсуа Вієта.

Історична довідка і презентація на комп’ютері.

Я вважаю, що до розв’язування певного типу  систем рівнянь можна застосовувати теорему обернену до теореми Вієта.

Суддя. Викликається наступний свідок.

Учитель. Розв’язати систему рівнянь графічним способом.  Побудову графіків виконуємо на комп’ютерах

Прокурор. Але цей метод знову можна використати тільки для відомих графіків функцій. І я не бачу жодних переваг в точності розв’язків системи.

Адвокат. Основна його перевага – наочність.

Учитель. Шановний суд. Існує ще метод для розв’язування систем рівнянь – це метод Гаусса.

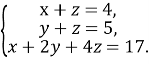
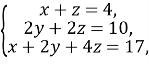
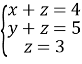
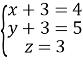
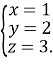
Прокурор. Але цей метод знову можна використати лише для систем лунійних рівнянь. І я не бачу переваг цього методу.

Адвокат. Основна його перевага – це компактність запису розв’язків..

 Суддя. Останнє слово підсудним.

Учень презентує розповідь про  Карла Фрідріха Гаусса.

Прокурор. Ознайомившись з різними способами розв’язування систем рівнянь, я не побачив переваг жодного з них над іншими..

Адвокат. Шановний суд, перш ніж засудити чи оправдати розглянуті способи і прийоми розв’язування систем рівнянь, прошу врахувати науковість, доступність і зручність застосування кожного з них.

Секретар. Прошу встати для оголошення вироку!

Суддя. Уважно заслухавши обидві сторони, суд постановив:

1. Усі розглянуті способи є суттєвими і доцільними. Кожен з них сприяє досягненню поставленої мети.
2. Жоден із способів не можна заперечити, і ,звичайно відкинути, адже кожному із них притаманна простота і витонченість.
3. Надалі невігласами будуть вважатися ті особи,які заперечують хочаб один із них.
4. Вивчення різних способів розв’язування систем рівнянь має важливе значення не лише для математики, а й для багатьох задач електротехніки, статистики та економіки.
5. Суд оправдовує всі способи розв’язування систем рівнянь.

Учитель. Отже, ми повинні виконувати постанову суду і вчитися обирати раціональний спосіб розв’язування систем рівнянь. А тому вдома ви розв’яжете дані системи, обираючи один із запропонованих способів.

ДЗ на індивідуальних картках.