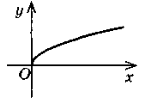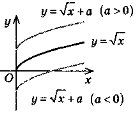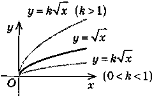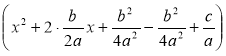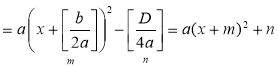Методичний кейс для дистанційного навчання з теми: "Квадратична функція".
Матеріал призначений для дистанційного навчання учнів, містить фрагменти відео-уроків для вивчення теоретичного матеріалу, стислі конспекти,, тестові завдання з відповідями для самоперевірки.
ТВОРЧА РОБОТА
(МЕТОДИЧНИЙ КЕЙС)
Розробка методичного е-контенту з теми: «Квадратична функція»
|
З. В. Кулик |
|
|
Описання теми
- Функції.
- Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції.
- Найпростіші перетворення графіків функцій.
-
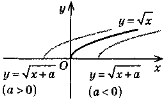
Функція y = а
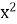 + bх + с, а ≠ 0, її графік і властивості.
+ bх + с, а ≠ 0, її графік і властивості.
- Квадратна нерівність.
- Розв'язування квадратних нерівностей.
- Розв'язування систем рівнянь другого степеня з двома змінними.
- Розв'язування текстових задач за допомогою систем рівнянь
Очікувані результати:
Учень/учениця:
- Обчислює значення функції в точці.
- Описує:
перетворення графіків функцій:
а) f(х) → f(х) + а;
б) f(х) → f(x + а);
в) f(х) → kf(x),
г) f(х) → - f(x) алгоритм побудови графіка квадратичної функції.
- Характеризує функцію за її графіком.
- Розв'язує вправи, що передбачають:
побудову графіка квадратичної функції;
побудову графіків функцій з використанням зазначених перетворень графіків;
використання графіка квадратичної функції для розв'язування квадратних нерівностей;
знаходження розв'язків систем двох рівнянь другого степеня з двома змінними;
складання і розв'язування систем рівнянь з двома змінними як математичних моделей текстових задач.
Вступний тест
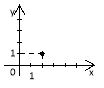 Графік якої з вказаних функцій проходить через задану точку:
Графік якої з вказаних функцій проходить через задану точку:
|
1 |
А |
Б |
В |
Г |
Д |
|
у = х+2 |
у = х–2 |
у = 2 |
у = х–1 |
у = х+1 |
|
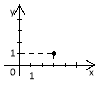
2 |
А |
Б |
В |
Г |
Д |
|
у = х+3 |
у = 3х |
у = х/3 |
у = 3 |
у = –3х |
|
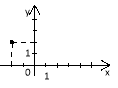
3 |
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
4. На якому з малюнків зображено графік функції y = kx + b, k>0, b>0
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
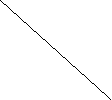
5. Визначте значення коефіцієнтів k і b функції y = kx + b
![]()
![]()
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
6. Який з графіків відповідає функції ![]() , якщо k<0
, якщо k<0
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
7. Знайти область визначення функції ![]()
|
А |
Б |
В |
Г |
Д |
|
(2; |
|
(4;+ |
|
|
8. ![]()
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
9. Знайти значення функції ![]() , якщо значення аргументу дорівнює 3.
, якщо значення аргументу дорівнює 3.
|
А |
Б |
В |
Г |
Д |
|
–1 |
–6 |
1 |
3,5 |
–3,5 |
10. При якому значенні аргументу значення функції ![]() дорівнює –2.
дорівнює –2.
|
А |
Б |
В |
Г |
Д |
|
–0,75 |
–1 |
–1,75 |
1,75 |
0 |
11. Яка з даних точок належить графіку функції ![]()
|
А |
Б |
В |
Г |
Д |
|
(–1; –4) |
(10; 1) |
(2; 4) |
(12; 2) |
(3; 15) |
Відповіді: 1) Г; 2) В; 3) Г; 4) А; 5) В; 6) А; 7) Г; 8) Г; 9) А; 10) Б; 11) Д.
Урок № 1
Тема уроку: Функції.
Мета уроку: повторити знання про означення, властивості числових функцій та приклади елементарних числових функцій і вигляд їхніх графіків. Сформувати знання про спосіб задання функції формулою у = f(x). Повторити та систематизувати вміння знаходити значення функції, що відповідає даному значенню аргументу, за даною формулою, і навпаки, а також уміння розв'язувати задачі на знаходження області визначення, області значень функції, а також умінь працювати з готовим графіком функції; виробити оперативні вміння роботи з формулою y = f(x).
Теоретичний матеріал
Функція — це залежність змінної у від змінної х, при якій кожному значенню х відповідає єдине значення у.
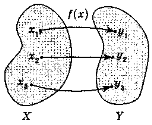
Позначається: y = f(x), де х — аргумент (незалежна змінна); у — функція, значення функції (залежна змінна); f(x0) — значення функції в точці х0.
Приклад. Дано функцію f(x) = ![]() - 3х + 2. Знайдемо: 1) f (0) 2) f (-1); 3) f (а).
- 3х + 2. Знайдемо: 1) f (0) 2) f (-1); 3) f (а).
Розв’язання
1) f (0) = 0 2 – 3 ∙ 0 + 2 = 2;
2) f (-1) = (-1) 2 – 3 ∙ (-1) + 2 = 6;
3) f (a) = a 2 – 3a + 2.
Область визначення функції D(f) — це множина всіх значень, яких набуває аргумент.
Як знайти область визначення функції y = f(x)
- Якщо f(x) — многочлен, то D(f) = R.
2. Якщо, ![]() знаходимо з умови: Q(x) ≠0 (знаменник дробу не дорівнює 0).
знаходимо з умови: Q(x) ≠0 (знаменник дробу не дорівнює 0).
3. Якщо ![]() , то D(f) знаходимо з умови: R(x) ≥ 0.
, то D(f) знаходимо з умови: R(x) ≥ 0.
|
Приклад. Знайдемо область визначення функції: |
|
Розв'язання |
|
1) 3х2 – х + 1 — многочлен, тому D(y) = R;
2)
3)
Отже, D(y) = (-∞; 0) Область значень функції E(f) — множина всіх значень змінної у, яких вона може набувати при всіх значеннях аргументу, взятих з D(f).
Приклад. Знайдемо область значень функції у = Розв'язання
При всіх x D(f) ≥ 0, тому Числовою функцією називають функцію, область визначення й область значень якої є числовими множинами. Графіком функції y = f(x) називають множину всіх точок координатної площини з координатами (х; f(x)), де х «пробігає» всю область визначення f(x) (a y — відповідне значення функції у точці х). |
Деякі елементарні функції та їхні графіки
|
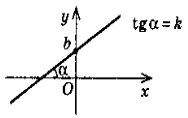
1. y = kx + b — лінійна функція
|
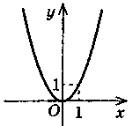
2. у = x2
|
|
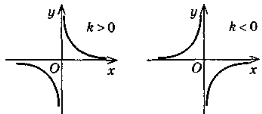
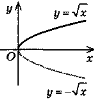
3. у =
|
4. y =
|
Питання для самоконтролю
- Сформулюйте означення функції.
- Що таке незалежна змінна, залежна змінна?
- Що таке графік функції?
- Що називають областю визначення і областю значень функції?
- Означення, графік та деякі властивості функцій:
- y = kx + b
-
у =
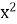
-
у =
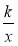
-
y =
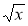
Виконати самостійно
- Через яку з даних точок проходить графік функції у = х2 + 2 ?
1) А(-2; 0); 2) В(-2; -2); 3) С(-2; 6); 4) D(-2; 2).
- Функцію задано формулою f(х) = 2х2 + 3х. Знайти: а) f(1); б) f(-4).
-
Функцію задано формулою f(х) = -2
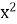 + 5х. Знайдіть значення аргументу, при якому значення функції дорівнює -3.
+ 5х. Знайдіть значення аргументу, при якому значення функції дорівнює -3.
- Областю визначення якої з наведених функцій є проміжок (9; + ∞)?
1) y = ![]() ; 2) у =
; 2) у = ![]() ; 3) у =
; 3) у = ![]() ; 4) у =
; 4) у = ![]() .
.
Відповіді: 1. 3); 2. а)5; б)20; 3. х = -0,5; х = 3; 4. 4)
Урок №2
Тема уроку: Функції. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції.
Мета уроку: сформувати знання про зміст понять: нулі функції, проміжки, на яких функція зберігає свій знак (проміжки знакосталості функції), функція, що спадає на проміжку, та функція, що зростає на проміжку. Сформувати вміння відтворювати означення вивчених понять, а також розв'язувати задачі на знаходження нулів функції та на дослідження функцій на зростання та спадання на проміжку з використанням вивченого на уроці означення.
Теоретичний матеріал
|
Властивості функції |
||
|
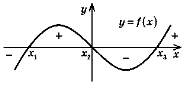
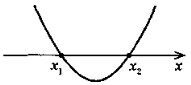
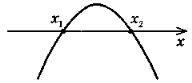
1. Якщо для функції y = f(x) виконується умова f (х0) = 0 (х0 |
||
|
|
На рисунку х1, х2, х3 — нулі функції ( f (x1) = f (x2) = f (x3) = 0). Проміжки (-∞; x1), (x1; x2), (х2; х3), (х3; +∞) — проміжки знакосталості функції y = f(x). |
|
|
2. |
|
|
|
|
||
|
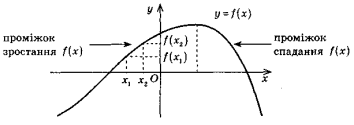
! Якщо необхідно визначити, чи є функція y = f(x) зростаючою/спадною на даному проміжку, то: |
||
|
а) покладають умову х2 > х1; |
||
|
б) записують різницю f(x2) – f(x1) та перетворюють її так, щоб можна було визначити її знак; |
||
|
в) якщо f(x2) – f(x1) > 0, то f(x2) > f(x1), і при умові х2 > х1 це означає, що f(x) зростає на даному проміжку; |
||
|
г) якщо f(x2) – f(x1) < 0, то f(x2)<f(x1), і при умові х2 > х1 це означає, що f(x) спадає на даному проміжку. |
||
Приклад. Знайти нулі та проміжки знакосталості функції у=3х+2
Розв’язання
-
у =0, 3х+2=0, х = -
 - нуль функції
- нуль функції
-
у
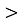
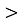
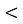
 . Отже у
. Отже у 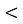
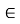
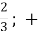 ∞)
∞)
-
у
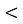
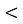
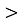
 . Отже у
. Отже у 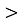
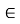
 )
)
Питання для самоконтролю
- Числова функція задається:
а) рівнянням у = f(x); б) областю визначення;
в) аргументом; г) графіком.
- У рівнянні y = f(x) число х — це:
а) аргумент; б) область визначення;
в) функція; г) область значення функції.
- Множина всіх точок з координатами (x; f(x)), де y = f(x) — задана функція, це:
а) точка; б) лінія;
в) f(x); г) графік функції y = f(x).
- Функція y = f(x) спадна, якщо:
а) х2 < х1; б) f(x2) < f(x1);
в) при х2 > х1 f(х2) < f(x1); г) при х2 < х1 f(x2) < f(x1).
- Функція y = f(x) зростаюча, якщо:
а) при х2 > х1 f(x2) > f(x1); б) у2 > у1;
в) при х2 > х1 f(x2) < f(x1); г) х2 > х1.
Виконати самостійно
- Яке з чисел (значень змінної х) є нулем функції у = 3х2 – 2х – 1:
1) 1; 2) -1; 3) ![]() ; 4)
; 4) ![]() ?
?
- Відомо, що y = f(x) спадає на всій області визначення. Порівняйте:
1) f (3) і f (-3); 2) f (-2) і f (-3,5); 3) f ![]() і f
і f ![]() .
.
- Відомо, що y = g(x) зростає на всій області визначення. Порівняйте:
1) g(1) і g(0,1); 2) g![]() і g
і g![]() .
.
-
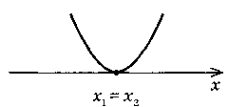
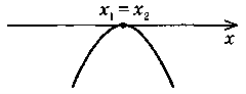
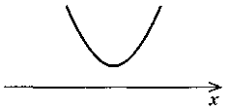
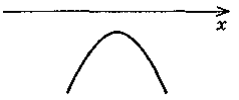
Відомо, що y = h(x) зростає, якщо х
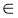 (-∞; 2], і спадає, якщо х
(-∞; 2], і спадає, якщо х 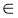 [2; +∞). Який із рисунків може бути зображенням графіка функції у = h(x)?
[2; +∞). Який із рисунків може бути зображенням графіка функції у = h(x)?
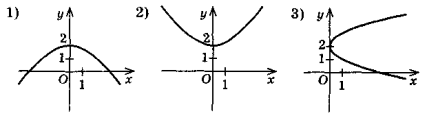
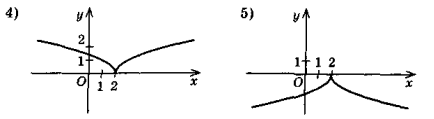
- На рисунку зображений графік функції, область визначення якої
D(f) = R. Укажіть:
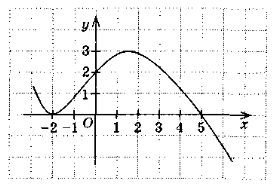
а) нулі функції;
б) проміжки ,на яких функція набуває додатних; від’ємних значень;
в) проміжки на яких функція зростає; спадає.
6. Знайти нулі функції: 1) у=![]() +10х-11; 2) у =
+10х-11; 2) у = ![]()
Відповіді: 1. 1);
2. 1) f (3) ![]()
![]()
![]()
![]()
![]() .
.
3. 1) g(1) ![]()
![]()
![]()
![]() .
.
4. 5)
5. а) ![]() =-2;
=-2; ![]() =5
=5
б) f(х) ![]()
![]()
![]()
f(х) < 0, х ![]() (5; +∞);
(5; +∞);
в) проміжок зростання x ![]() [-2; 2]
[-2; 2]
проміжок спадання х ![]()
![]() ;
; ![]()
6. 1)![]() =-11;
=-11; ![]() =1
=1
7. 2)![]() =-3;
=-3; ![]() =3
=3
Урок №3
Тема уроку. Найпростіші перетворення графіків функцій.
Мета уроку: сформувати розуміння змісту поняття «перетворення графіка функції», а також розуміння того факту, що певне перетворення рівняння функції тягне за собою перетворення графіка та навпаки. Сформувати знання про основні види геометричних перетворень графіків функцій (на інтуїтивному рівні) та про рівняння функції, що задається цим перетворенням. Сформувати первинні уміння «читати» графіки функцій (тобто за готовими графіками задавати рівняння функцій), а також виконувати побудови графіків функцій за допомогою перетворень, заданих рівнянням даної функції.
Мотивація навчальної діяльності учнів
Дослідження функцій за готовим графіком є більш простим, ніж за формулою. В ряді випадків для розв'язування задач необхідно буває побудувати графік функції, яка не є елементарною. Отже, формулюється питання: чи існують засоби (і якщо існують, то як ними користуватися), за допомогою яких можна побудувати графік деякої функції, використовуючи при цьому вміння будувати графіки елементарних функцій (лінійної, оберненої пропорційності, квадратичної функції та функції у = ![]() ).
).
Теоретичний матеріал
|
Найпростіші перетворення графіків функцій |
|||
|
№ з/п |
Формула залежності |
Приклад |
Перетворення |
|
1 |
y = -f(х) |
|
Симетрія відносно осі Ох |
|
2 |
y = f(х) + a |
|
Паралельне перенесення вздовж осі Оу на а одиниць (якщо а > 0, то вгору, якщо а < 0, то вниз) |
|
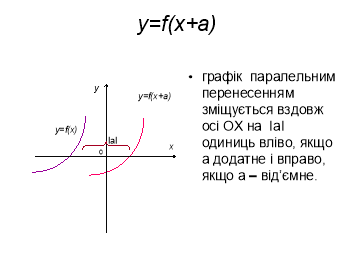
3 |
y = f(х + a) |
|
Паралельне перенесення вздовж осі Ох на +а одиниць (якщо а > 0 — вліво, якщо а < 0 — вправо) |
|
4 |
y = kf(х) (k > 0) |
|
Той самий вигляд, що і y = f(x), тільки розтяг-нуто, якщо k > 1, і стиснуто, якщо 0 < k < 1 |
Приклади:
-
Побудувати графік функції у =
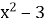
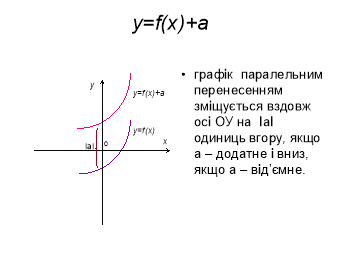

-
Побудувати графік функції
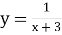

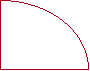
- Побудувати в одній системі координат графіки функцій: у=х2, у=2х2 та у=0,5х2.
Приклад графіка функції у = кf(x)
Складемо таблиці:
|
х |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
у=х2 |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
|
у=2х2 |
18 |
8 |
2 |
0 |
2 |
8 |
18 |
|
у=0,5х2 |
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
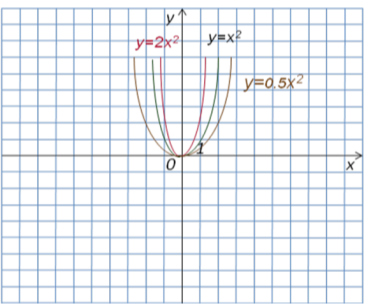
Висновок: щоб побудувати графік даної функції потрібно стиснути (якщо к менше одиниці) або розтягнути (якщо к більше одиниці) графік початкової функції відносно осі ОХ.
Зауваження: для побудови більш складних функцій потрібно виконати послідовно геометричні перетворення декілька разів.
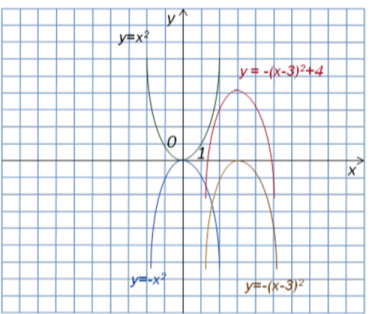
- Побудувати графік функції: у= -(х-3)2+4.
Для цього виконаємо послідовно такі перетворення:
- Графік початкової функції у=х2 симетрично відобразимо відносно вісі ОХ.
- Графік отриманої функції у=-х2 за допомогою паралельного перенесення зміщуємо вправо на 3 одиниці.
- Графік функції у=-(х-3)2 паралельним перенесенням зміщуємо вгору на 4 одиниці.
Виконати самостійно
- В одній системі координат побудувати графіки функцій:
а) у = ![]() +2 та у =
+2 та у = ![]() -2
-2
б) у = ![]() - 1 та у =
- 1 та у = ![]() + 3
+ 3
в) у = х2 + 1 та у = х2 - 1
г) у =![]() та у =
та у = ![]()
д) у= (х+1)2 та у= (х-4)2
е) у = ![]() та у =
та у = ![]() :
:
Відповідь: https://youtu.be/N6zTRBS0r_g
Урок №4
Тема уроку. Функція ![]() , її властивості та графік.
, її властивості та графік.
Мета уроку: сформувати знання про означення, вид графіка та алгоритм побудови графіка квадратичної функції. Сформувати первинні вміння розпізнавати квадратичну функцію серед інших елементарних функцій, знаходити координати вершини та напрям віток графіка квадратичної функції, виконувати побудову графіка квадратичної функції за вивченими алгоритмами. Повторити загальні властивості функцій, а також схеми виконання основних видів геометричних перетворень графіків функцій.
Усні вправи
- Як побудувати графік функції у = 2х2, маючи графік у = х2.
-
Як побудувати графік функції у =
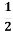 х2, маючи графік у = х2.
х2, маючи графік у = х2.
- Як побудувати графік функції у = (х-2)2, маючи графік у = х2.
- Як побудувати графік функції у = х2+3, маючи графік у = х2.
- Як побудувати графік функції у = - х2, маючи графік у = х2.
- Яку функцію ми отримаємо, якщо графік функції у = х2 паралельним перенесенням змістити на 3 одиниці вліво та 2 одиниці вниз?
- Яку функцію ми отримаємо, якщо графік функції у = х2 симетрично відобразити відносно вісі ОХ і стиснути його до вісі ОХ в три рази?
- Розв’яжіть рівняння х2- 9 = 0.
- Розв’яжіть рівняння х2 + 6х = 0.
- Розв’яжіть рівняння х2- 5х + 6 = 0.
- Розв’яжіть рівняння х2+6х+9 = 0
Теоретичний матеріал
|
Функція виду у = ax2 + bx + c, де а |
|||
|
Наприклад: |
|||
|
Графік квадратичної функції — парабола, вітки якої напрямлені вгору, якщо а > 0, і вниз — якщо а < 0 . |
|||
|
Координати вершини (х0; у0) параболи графіка у = ах2 + bх + с обчислюються за формулами: |
|||
|
|
|||
|
Наприклад: у функції у = х2 + 2х – 3, яка є квадратичною, графік — парабола. Вітки параболи напрямлені вгору (а = 1 > 0), а координати вершини: |
|||
|
|
|||
|
або y0 = f (-1) = (-1)2 + 2 ∙ (-1) – 3 = 1 – 2 – 3 = -5 + 1 = -4. |
|||
|
Тобто вершина параболи (-1; - 4). |
|||
|
|
Побудова графіка функції у = ах2 + bх + с, а |
||
|
|
Спосіб 1 |
Спосіб 2 |
|
|
|
1. Обчислити абсцису вершини |
1. Виділити повний квадрат:
ах2 + bх + с = а |
|
|
|
2. Підставити х0 у рівняння і знайти у0. 3. Побудувати параболу у = ах2 з вершиною в точці (х0; у0). Якщо а > 0, вітки параболи напрямлені вгору, якщо а < 0 — вниз. 4. Для більшої точності побудови знайти точки перетину графіка з координатними осями. |
= а 2. Використавши схему геометричних перетворень графіків функцій, виконати побудову параболи у = х2, потім її розтягнення (або стиснення) до параболи у = ах2, а потім виконати паралельне перенесення у = ах2 вздовж осі Ох на – т і вздовж осі Оу на п. |
|
Розв’язуємо вправу разом.
- Подувати графік функції у = х2 - 10х + 22 та за допомогою графіка вказати проміжки монотонності та найменше значення, яке може приймати функція.
Виділимо квадрат двочлена з тричлена:
х2 - 10х + 22 = х2 - 10х + 25 – 3 = (х-5)2 – 3.
Отже графік функції у = х2 спочатку потрібно змістити паралельним перенесенням на 5 одиниць вправо, а потім на 3 одиниці вниз.
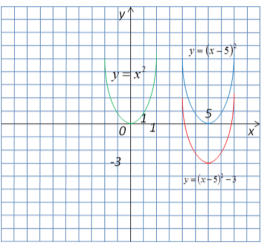
Функція спадає при значенні аргуменнта ( - ∞; 5 ); зростає при ( 5; + ∞).
Найменше значення, що приймає функція це у= –3.
Зауваження: при виділенні квадрата двочлена з квадратного тричлена можна визначити координати вершини параболи. В даному випадку це – (5;-3).
Даний графік можна було побудувати і іншим способом: перенести систему координат у вершину параболи (5;-3) і в новій системі координат побудувати графік функції у = х2
Розв’язуємо вправу разом.
- Подувати графік функції у = 2х2 + 4х + 4.
Виділимо квадрат двочлена з тричлена: 2х2 + 4х + 4 = 2(х2 + 2х + 1) + 2 = 2(х + 1)2 + 2.
Перенесемо систему координат у точку (-1;2), що є вершиною параболи і в цій новій системі координат побудуємо графік функції у = 2х2.
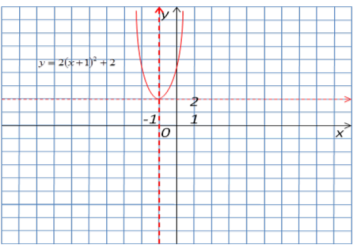
Можна будувати графік квадратичної функції у = ах2 + bх + с і без виділення повного квадрата за наступним алгоритмом:
- Якщо а>0, то вітки вгору, якщо а<0, то вітки вниз.
- Знаходимо нулі функції (точки перетину графіка з віссю ОХ) – корені квадратного рівняння ах2 + bх + с = 0.
-
Знаходимо абсцису вершини параболи
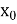 = -
= -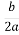
- Знаходимо ординату вершини параболи – значення функції при
![]() = -
= -![]() .
.
- Знаходимо точку перетину параболи з віссю ОУ: у = с.
Розв’язуємо вправу разом.
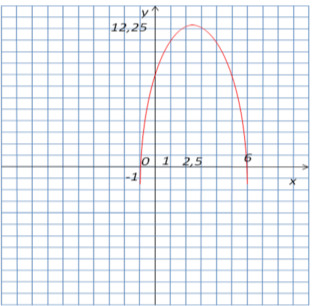
Побудувати графік функції у = -х2 + 5х + 6 і вказати всі її властивості.
а = - 1 – парабола вітками вниз.
- х2 + 5х + 6=0;
х2 – 5х – 6 =0;
х = -1, х = 6 – абсциси точок перетину з віссю Ох.
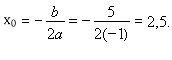
![]() .
.
у = 6 – ордината точки перетину з віссю ОУ.
Контрольні запитання
-
Опишіть, що являє собою графік функції:
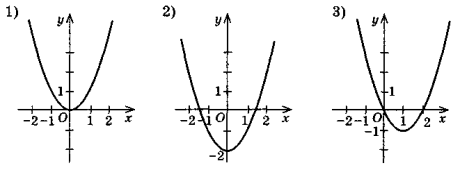
1) y = х2; 2) у = 2х2; 3) y = 2(x – 1)2 + 1; 4) у = 2х2 – 4х + 1. - Який із наведених графіків відповідає рівнянню у = х2 – 2х? Відповідь обґрунтуйте.
Розв’язати вправи.
- Визначити напрям віток, знайти координати вершини і побудувати схематично графік квадратичної функції у = х2 - 10х + 20.
- Побудувати графік функції у = -0,2х2 + 2х – 5. Знайти нулі функції та значення х, при яких f(х)= -5.
- Побудувати графік функції f(х)= 6х-2х2. Користуючись графіком функції, знайти розв’язки нерівності f(х)≥0, f(х)<0.
-
Зобразити схематично графік функції у = ах2 + bх + с, якщо а<0, D=0,
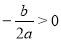 .
.
- Знайти проміжки зростання та спадання функції у=х2-16.
- На параболі у=-х2+5х+5 знайти точку, у якої абсциса і ордината рівні.
- *Подувати графік функції у = х2 - 4|х| + 3.
Відповідь:
-
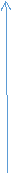 а = 1
а = 1 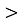
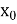 = 5,
= 5, 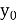 = -5
= -5
у

![]() 5 х
5 х
-5
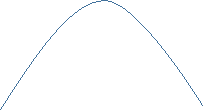
-
а = - 0,2
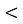
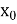 = 5,
= 5, 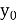 = 0
= 0
точка перетину з OY (0;-5)
при f(х)= -5, х=0, х=10
![]()
![]() у
у
 5 х
5 х
-5
-
а = - 2
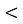
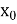 = 1,5,
= 1,5, 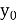 = 3,5
= 3,5
точка перетину з OY (0;0)
точки перетину з OX (0;0) та (0;3)
![]() у
у
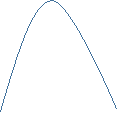 3,5
3,5
![]()
0 3 х
f(х)≥0, x ![]() [0; 3]
[0; 3]
f(х)<0, х ![]()
![]()
![]()
![]() 4. у
4. у
 х
х
-
у=х2-16 зростає при x
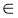 [0;
[0; 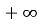
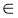 (
(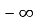
- (5;5); (-1;-1)
-
 у
у

3
![]()
-3 -1 0 1 3 х
Урок № 5
Тема уроку. Функція ![]() , її властивості та графік.
, її властивості та графік.
Мета уроку: закріпити знання про означення, вид графіка та алгоритм побудови графіка квадратичної функції. Дослідити властивості квадратичної функції та узагальнити ці спостереження, доповнивши ними знання про властивості квадратичної функції. Закріпити вміння розпізнавати квадратичну функцію серед інших елементарних функцій, знаходити координати вершини та напрям віток графіка квадратичної функції, виконувати побудову графіка квадратичної функції за вивченими алгоритмами. Виробити вміння застосовувати виконані на уроці спостереження для аналітичного дослідження властивостей квадратичної функції загального вигляду. Повторити загальні властивості функцій, а також схеми виконання основних видів геометричних перетворень графіків функцій.
Перевір себе:
- З графіка якої функції виду у = ах2 можна отримати паралельним перенесенням графік функції:
у = -3х2 + 5х – 4;
- Укажіть координати вершини параболи:
у = -х2 + 6х – 8;
- Чи перетинає вісь абсцис графік функції:
у = -х2 + х – 6;
- Вгору чи вниз напрямлені вітки параболи:
у = ![]() х2 + 2х + 5;
х2 + 2х + 5;
- Побудуйте ескіз графіка функції:
у = х2 – 6х + 8;
-
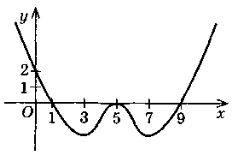
На рисунку зображено графік функції f. Визначте:
- при яких х функція зростає; спадає;
- при яких х функція набуває значень, що дорівнюють нулю, більші нуля, менші нуля;
- при яких значеннях х на відрізку [1;7] функція набуває найменшого значення, найбільшого значення.
Теоретичний матеріал
Властивості функції закладені в її рівняння та можуть бути визначені й без побудови графіка, тобто аналітично.
|
Властивості квадратичної функції
(функції виду у = ax2 + bx + c, а |
|
|
а > 0 |
а < 0 |
|
1. D(y) = R 2. Е(у) = [у0; +∞) |
1. D(y) = R 2. Е(у) = (-∞; y0] |
|
(у0 — ордината вершини параболи) |
|
|
3. а) Функція зростає, якщо
х б) Функція спадає, якщо
х |
3. а) Функція зростає, якщо
х б) Функція спадає, якщо
х |
|
(х0 — абсциса вершини параболи) |
|
|
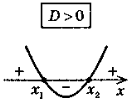
4. а) Якщо D > 0, то
у > 0 при х
у < 0 при x
|
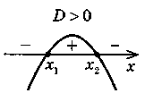
4. а) Якщо D > 0, то
у > 0 при х
у < 0 при x
|
|
(х1, х2 – нулі функції) |
|
|
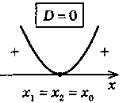
б) Якщо D = 0, то у > 0
при х
|
б) Якщо D = 0, то у < 0
при х
|
|
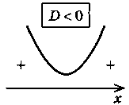
в) Якщо D < 0, то у > 0 при x
|
в) Якщо D < 0, то у < 0 при х
|
Знання теоретичної частини.
- Від якого коефіцієнта квадратного тричлена у записі квадратичної функції залежить напрям віток параболи?
- Вказати формулу для обчислення абсциси вершини параболи.
- Як знайти ординату вершини параболи.
- Скільки точок перетину з віссю ОХ має парабола, якщо дискримінант відповідного рівняння від’ємний?
- Скільки точок перетину з віссю ОХ має парабола, якщо дискримінант відповідного рівняння додатний?
- Скільки точок перетину з віссю ОХ має парабола, якщо дискримінант відповідного рівняння дорівнює 0?
- Як знайти точку перетину з віссю ОУ квадратичної функції
у = ах2 + bх + с?
- Чому дорівнює найбільше значення квадратичної функції
у = ах2 + bх + с, якщо а<0?
- Чому дорівнює найменше значення квадратичної функції
у = ах2 + bх + с, якщо а>0?
Розв’язуємо вправу разом.
- З’ясувати, якого значення(найбільшого чи найменшого) набуває функція у=1,5х2 -6х + 1 в точці екстремуму і обчислити це значення.
Розв’язання:
Оскільки а=1,5![]()
![]() = -
= -![]() = 2 ;
= 2 ; ![]() =1,5
=1,5 ![]()
![]() – 6 · 2 + 5 = -5
– 6 · 2 + 5 = -5
Відповідь: функція набуває найменшого значення -5 в точці екстремуму.
- Вказати інтервали зростання і спадання функції у=-х2 -5х -4.
Розв’язання:
Оскільки а=-1![]()
![]()
![]() ), де
), де ![]() - абсциса вершини параболи, функція зростає, а на проміжку (
- абсциса вершини параболи, функція зростає, а на проміжку (![]() ;+
;+![]()
![]() :
:
![]() = -
= -![]() = -2,5
= -2,5
Відповідь: функція у=-х2 -5х -4 зростає на проміжку (![]()
![]()
Розв’язати вправи.
- Користуючись малюнком виконайте завдання 1-10:
- Укажіть знак коефіцієнта а.
- Укажіть координати вершини параболи.
- Знайдіть вісь симетрії параболи.
- Знайдіть нулі функції.
- Укажіть проміжки, на яких функція набуває додатних значень.
- Укажіть проміжки, на яких функція набуває від’ємних значень.
- Укажіть проміжок, на якому функція зростає.
- Укажіть проміжок, на якому функція спадає.
- Визначте знак коефіцієнта с.
- Визначте знак коефіцієнта b.
![]() у
у
![]()
![]() -4 -2 -1 0 1 2 х
-4 -2 -1 0 1 2 х
-8
-9
2. Не виконуючи побудови графіка функції у=![]() -6х +8 встановіть:
-6х +8 встановіть:
1. якого значення(найбільшого чи найменшого) набуває функція точці екстремуму і обчислити це значення;
2. вказати інтервали зростання і спадання функції.
Відповідь:
-
1. а
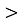
2. (-1;-9)
3. х=-1
4. -4; 2.
5. (-![]()
![]()
![]()
6. (-4;2)
7. ![]() ;+
;+![]()
8. (-![]()
![]()
9. с![]()
10. b![]()
2. 1. в точці екстремуму функція набуває найменшого значення ![]() =3,
=3, ![]() =-1.
=-1.
2. функція у=х2 -6х +8 зростає на проміжку (3;+![]()
функція у=х2 -6х +8 спадає на проміжку (-![]()
УРОК № 6
Тема уроку. Квадратна нерівність. Розв'язування квадратних нерівностей.
Мета уроку: сформувати знання учнів про зміст поняття «квадратна нерівність», домогтися розуміння та засвоєння учнями схеми розв'язування квадратних нерівностей із використанням побудови графіка квадратичної функції. Сформувати первинні вміння вирізняти квадратні нерівності серед інших нерівностей з однією змінною; за готовими графіками квадратичної функції знаходити розв'язки відповідних квадратних нерівностей, а також виконувати послідовні дії відповідно до вивченої схеми для відшукання розв'язків квадратних нерівностей різного виду.
Усні вправи
- Серед наведених рівнянь укажіть рівняння, що задають квадратичну функцію:
1) у = 2х2 + х – 1; 2) у2 = х + 1; 3) у2 = х2 – 1;
4) у = -х – х2; 5) у2 = х2; 6) у = -х2.
Для вказаних функцій назвіть коефіцієнти квадратного тричлена (у формулі у = ах2 + bх + с).
- Дано умови:
а) а > 0; D > 0; c < 0; б) а > 0; D = 0; c > 0;
в) а < 0; D < 0; c < 0; г) а < 0; D > 0; c = 0;
д) а > 0; с = 0; D = 0.
Із запропонованих рисунків графіків функції у = ах2 + bх + с оберіть той, що задовольняє кожну з даних умов:
-
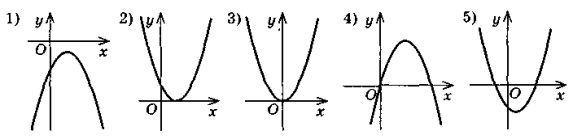
Знайдіть нулі функції (якщо вони існують):
1) у = 2х – 3; 2) у =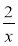 ; 3) у =
; 3) у = 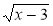 ; 4) у = х2 – 3х + 2.
; 4) у = х2 – 3х + 2.
Теоретичний матеріал
План вивчення нового матеріалу
- Означення квадратної нерівності. Приклади квадратних нерівностей з різними коефіцієнтами.
- Схема розв'язування квадратних нерівностей за допомогою побудови графіка відповідної квадратичної функції.
- Різні способи розташування графіка квадратичної функції y = ax2 + bx + c відносно осі Ох залежно від знака старшого коефіцієнта та знака дискримінанта квадратного тричлена ах2 + bх + с.
|
|
Нерівності виду ах2 + bх + с > 0 (<0; ≥ 0; ≤ 0) називаються квадратними, якщо а |
|
||
|
|
Приклад. 3х2 – 2х – 1 > 0, x2 – 9 ≥ 0, х2 – 2х < 0, -х2 > 0 — квадратні нерівності (з різними значеннями коефіцієнтів квадратного тричлена в лівій частині). |
|
||
|
|
Схема розв'язування квадратних нерівностей |
|
||
|
|
1. Знайти дискримінант D, а потім корені x1, x2 квадратного тричлена (якщо вони існують). |
|
||
|
|
2. Побудувати ескіз графіка квадратичної функції у = ах2 + bх + с (з урахуванням знака коефіцієнта а та знайденого знака дискримінанта D і коренів). |
|
||
|
|
3. Для випадку > 0 відповідно отримаємо проміжок, для якого точки параболи лежать вище осі Ох, для випадку < 0 відповідно отримаємо проміжки, для яких точки параболи лежать нижче осі Ох. |
|
||
|
|
Схема розв'язування нерівності ах2 + bx + c > 0 залежно від а і D |
|
||
|
|
ax2 + bx + c > 0 (D = b2 – 4ac)
|
|
||
|
|
x |
x |
x |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
х |
x |
x |
|
|
|
|
|
|
|
Розв’язуємо вправи разом
Усні вправи
- Дано нерівності:
а) ах2 + bx + c > 0; б) ах2 + bx + c < 0;
в) ах2 + bх + с ≥ 0; г) ах2 + bx + c ≤ 0.
Знайдіть розв'язок кожної з даних нерівностей за графіком функції
у = ах2 + bх + с, зображеним на рисунку:
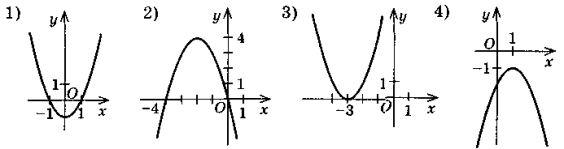
Розв’язання:
1) а) (–∞; –1)U(1; ∞) б) (–1; 1) в) (–∞; –1]U[1; ∞) г) [–1; 1]
2) а) (–4; 0) б) (–∞; –4)U(0; ∞) в) [–4; 0] г) (–∞; –4]U[0; ∞)
3) а) (–∞; –3)U(–3; ∞) б) в) (–∞; ∞) г) –3
4) а) б) (–∞; ∞) в) г) (–∞; ∞)
-
Чи є число: 0;
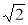 ; –3 — розв'язком нерівності:
; –3 — розв'язком нерівності:
1) 2х + 3 < 0; 2) х2 ≤ 0; 3) х2 > 2?
Розв’язання:
- 2·0+3 < 0 – нерівність невірна, отже х=0 – не є розв’язком нерівності.
2·![]() +3 < 0 – нерівність невірна, отже х=
+3 < 0 – нерівність невірна, отже х=![]() – не є розв’язком.
– не є розв’язком.
2·(–3)+3 < 0 – нерівність вірна, отже х=–3 – є розв’язком нерівності.
-
x=0 – розв’язок нерівності;
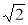 та –3 – не є розв’язками.
та –3 – не є розв’язками.
-
x=–3 – розв’язок нерівності;
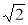 та 0 – не є розв’язками.
та 0 – не є розв’язками.
- Яка з нерівностей не є квадратною?
1) х2 – 44 > 0; 2) х2 + 3 < 0; 3) х2 + 3х3 > 0; 4) -х2 – 5 ≤ 0.
Письмові вправи
- Розв’язати нерівність х2–5х+6 > 0.
Розв’язання:
- Знаходимо нулі функції, для чого розв’язуємо рівняння х2–5х+6 = 0.
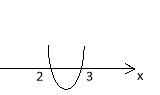 D=25–24=1
D=25–24=1
x1=2; x2=3
- Будуємо ескіз графіка (враховуючи а=1 > 0, гілки вгору)
- За графіком знаходимо проміжки, для яких точки параболи розташовані вище вісі ОХ (за умовою у>0).
Відповідь: (–∞; 2) U (3; ∞)
- Розв’язати нерівність (1–х)(х+3)–16 ≤ 5х.
Розв’язання:
- Розкриваємо дужки, переносимо доданки в ліву частину, приводимо подібні доданки. Отримаємо нерівність х–х2–3х+3–16–5х ≤ 0.
–х2–7х–13 ≤ 0.
Знаходимо нулі функції, для чого розв’язуємо рівняння –х2–7х–13 = 0.
х2+7х+13 = 0
D=49–52<0
Корнів не має.
- Будуємо ескіз графіка (враховуючи а=–1 < 0, гілки вниз)
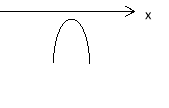
- За графіком знаходимо проміжки, для яких точки параболи розташовані нижче вісі ОХ (за умовою у ≤ 0).
Відповідь: (–∞; ∞)
Контрольні запитання
- Визначте знак коефіцієнта а, коефіцієнта с, дискримінанта D за графіком функції у = ах2 + bх + с, зображеним на рисунку:
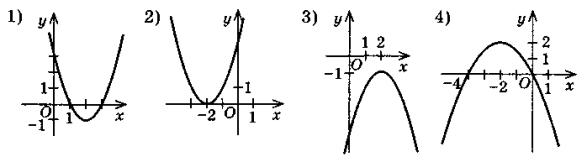
- Яка квадратна нерівність має розв'язком проміжок (див. рисунки вище):
1) x ![]() [1; 3]; 2) x
[1; 3]; 2) x ![]() R;
R;
3) х ![]() (-∞; -4)
(-∞; -4) ![]() (0; +∞); 4) розв'язків немає.
(0; +∞); 4) розв'язків немає.
Тренувальні вправи
Розв’яжіть нерівності:
1) -х2-4х-3 < 0 Відповідь: (–∞; -3) U (-1; ∞)
2) х2+2х-8 ≤ 0 Відповідь: [-2; 4]
3) х2-6 ≥ 3 Відповідь: (–∞; -3] U [3; ∞)
4) х2+4х-12 > 2(х-2) Відповідь: (–∞; -4) U (2; ∞)
5) (2х+9)(х-4)-(х+6)(х-11) ≥ 37 Відповідь: (–∞; -7) U (1; ∞)
6) (2х+7)(х-2)-(х+4)(х-5) ≤ 18 Відповідь: [-6; 2]
7) ![]() Відповідь: [–2; -1) U (-1; 1]
Відповідь: [–2; -1) U (-1; 1]
УРОК № 7
Тема уроку. Квадратна нерівність. Розв'язування квадратних нерівностей.
Мета уроку: закріпити знання учнів про зміст означення квадратних нерівностей та схему їх розв'язування; удосконалити вміння учнів розв'язувати квадратні нерівності та нерівності, що зводяться до квадратних шляхом рівносильних перетворень, а також виробити вміння використовувати ці вміння під час розв'язування систем квадратних нерівностей та для розв'язування задач дослідницького характеру.
Усні вправи
- Розв'яжіть рівняння (за теоремою Вієта):
1) x2 – 2х + 1 = 0; 2) х2 – 2х = 0; 3) 3х – 2 = 0;
4) х2 – 5x + 4 = 0; 5) 3 – x – 2х2 = 0; 6) х2 – 2х + 5 = 0.
- Знайдіть переріз та об'єднання числових проміжків, зображених на рисунку:
|
1) |
|
2) |
|
|
3) |
|
4) |
|
-
Знайдіть розв'язок системи:
1)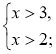 2)
2) 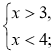 3)
3) 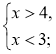 4)
4) 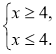
- Дано вирази:
а) ![]() ; б)
; б) 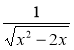 ; в)
; в) ![]() .
.
Укажіть нерівність, яка є записом умови існування кожного з даних виразів:
1) х ≥ 0; 2) х > 0; 3) ![]() ≥ 0; 4) 4х2 – 2х ≥ 0; 5) х2 – 2х > 0.
≥ 0; 4) 4х2 – 2х ≥ 0; 5) х2 – 2х > 0.
- Який із записів є умовою існування двох різних дійсних коренів рівняння х2 – 3ах + а2 = 0?
1) 9а2 – а2 > 0; 2) 9а2 – 4а2 > 0; 3) 9а2 – 4а2 ≥ 0; 4) 9а2 – 4а2 < 0.
Письмові вправи
Завдання 1
Знайдіть область визначення функції:
1) у = ![]() ; 2) у =
; 2) у = 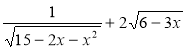 .
.
Розв’язання:
- З умови існування арифметичного квадратного кореня треба розв’язати нерівність х2+х–2 ≥ 0. Відповідь: (–∞; –2] U [1; ∞)
-
З умови існування арифметичного квадратного кореня та дробу отримаємо систему нерівностей:
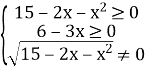 , яка рівносильна системі
, яка рівносильна системі  .
.
![]()
![]()
![]()
![]()
![]() Розв’язуємо окремо кожну нерівність і знаходимо перетин проміжків, які є розв’язками нерівностей.
Розв’язуємо окремо кожну нерівність і знаходимо перетин проміжків, які є розв’язками нерівностей.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: (–5; 2]
Завдання 2 (поглибленого рівня)
Знайдіть усі значення параметра а, при яких рівняння х2 – (а + 1)х + а2 = 0 має два різні дійсні корені.
Розв’язання:
Рівняння має два різні дійсні корені, коли D>0.
(a+1)2 – 4a2 > 0
–3a2 + 2a +1 > 0
Відповідь: (–1/3; 1)
Тренувальні вправи
Знайдіть область визначення функції:
1) у = ![]() ; 2) у =
; 2) у = 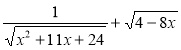 .
.
Відповідь: 1) [–2; 7]; 2) (–∞; –8) U (–3; 0,5]
При яких значеннях параметру а рівняння 3х2 – ах + 2а = 0 не має дійсних коренів.
Відповідь: (0; 24)
Подивитись презентацію за даною темою можна за посиланням
http://www.metod-kopilka.ru/prezentaciya_quotreshenie_kvadratnyh_neravenstvquot_9_klass-13675.htm
Щоб систематизувати знання перед контрольною роботою, можна переглянути презентацію
http://uslide.ru/algebra/15965-kvadratichnaya-funkciya-klass.html
УРОК № 8
Тематична контрольна робота.
«Функції. Властивості функції. Функція у = ах2 + bx + c».
«Розв'язування квадратних нерівностей».
- Дана функція f(x) = x2–4x+2. Знайти f(–3).
|
А |
Б |
В |
Г |
Д |
|
–1 |
20 |
–4 |
23 |
–38 |
- Чи проходить графік функції у = х2+6х–2 через точку А (3; 23)? (Так, Ні)
- Знайти координати вершини параболи – графіка функції у = х2–8х+7.
|
А |
Б |
В |
Г |
Д |
|
(4; 11) |
(–4; –11) |
(–4; 11) |
(4; –11) |
(–8; 7) |
- У якій точці вісь ОY перетинається з графіком функції у = х2+5х+6?
|
А |
Б |
В |
Г |
Д |
|
5 |
6 |
2,5 |
2;3 |
-2,5 |
- У якій точці вісь OX перетинається з графіком функції у = х2–5х +6?
|
А |
Б |
В |
Г |
Д |
|
6 |
2 |
3 |
2;3 |
2,5 |
-
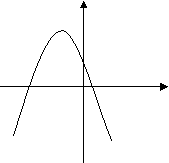
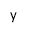 Визначити знаки коефіцієнтів a, b, c для функції y = ax2 + bx + c , яка задана графіком
Визначити знаки коефіцієнтів a, b, c для функції y = ax2 + bx + c , яка задана графіком
![]()
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- Якому графіку відповідає функція y = ax2 + bx + c, якщо відомо, що a>0, b>0, c>0
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
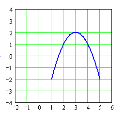
8. Графік якої з функцій зображено на малюнку?
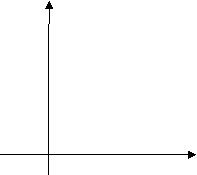 А) у=х2+2 Б) у=(х–2)2 В) у=(х–2)2+2 Г) у=(х+2)2–2 Д) у=(х+2)2+2
А) у=х2+2 Б) у=(х–2)2 В) у=(х–2)2+2 Г) у=(х+2)2–2 Д) у=(х+2)2+2
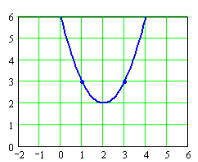
9. На якому з малюнків зображений графік функції у = –(х+3)2+2 ?
![]()
 А) Б) В) Г) Д)
А) Б) В) Г) Д)
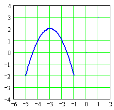
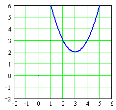
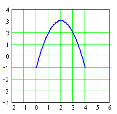
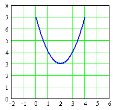
10.Знайти область визначення функції ![]()
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
11. Розв’язати нерівність ![]()
- Побудувати графіки функцій:
- у=8–2х–х2 2) у= х2–4·|x|+3
Відповіді: 1) Г 2) Ні 3) Г 4) Б 5) Д 6) Г 7) В 8) В 9) Б 10) Б
11) [–2; 1) U (1; 4]


про публікацію авторської розробки
Додати розробку