Урок "Способи задання функцій. Графік функції. Монотонність, парність і непарність функцій"

Тема заняття: Способи задання функцій. Графік функції. Монотонність, парність і непарність функцій.

Мета заняття: узагальнити і систематизувати знання студентів про способи задання функцій. Удосконалювати вміння досліджувати функції на монотонність аналітично і користуючись графіками.

Тип заняття: лекція комплексного характеру.

Обладнання: підручники, опорні конспекти, презентація «Парні  і непарні функції»

Література:

1. Алгебра і початки  аналізу: підруч. для 10 кл. загальноосвіт. навч. закладів М.І. Шкіль, З.І. Слєпканеь, О.С. Дубинчук.-К.: Зодіак – ЕКО, 2007. – 272 с.

2. Математика: Підручник О.М. Афанасьєва, Я.С. Бродський, О.Л. Павлов,  А.К.Сліпченко – К.: Вища школа, 2001.-447 с.

3. Чекова А.М. Алгебра. 7-12 класи: Навчальний посібник – 5-те видавництво.-Х.: Країна лерій. 2007.-120 с.

План заняття

I. Організація початку заняття.

ІI. Актуалізація опорних знань:

• Усне опитування студентів;
• Перевірка виконання домашнього завдання.
• Робота за індивідуальними картками.

ІІI. Систематизація  знань студентів. Виконання вправ.

IV. Підведення підсумків заняття.

V. Домашнє завдання.

Хід заняття

I. Організація початку заняття.

ІI. Актуалізація опорних знань:

1. Питання до усного опитування:

- Як можна задавати функцію?

- Що називають нулями функції?

- Які функції називаються зростаючими? А спадними?

- Чи може функція на одному проміжку спадати, а на іншому – зростати?

2. Перевірка виконання домашнього завдання.

3. Робота за індивідуальними картками:

Картка №1.

1. Функцію задано формулою , знайти : f (1), f (0), f(-3).

2. Знайти область визначення функції, заданої формулою:

а) ;    б)

3. Чи є парною або непарною функція, задана формулою:

а) ;   б)

Картка № 2.

 1. Функцію задано формулою , знайти: f (2), f (0), f (-2).

 2. Знайти область визначення функції, заданої формулою:

а) ;  б)

3. Побудувати графік функції, знайти проміжки, в яких функція зростає, і проміжки, в яких вона спадає:

а)

Картка №3.

1. Знайти область визначення функції, заданої формулою:

а) ;      б)

2. Чи є парною або непарною функція, задана формулою:

а) ;     б) ;     в)

ІІI. Систематизація  знань студентів. Виконання вправ.

1. Не виконуючи побудову, знайти координати точок перетину графіка функції з осями координат.

Розв’язання . Щоб  знайти точку перетину графіка з віссю , необхідно розв’язати рівняння у=0.

-2х -8=0

-2х=8

х=-4

(-4;0) – точка перетину з віссю  .

Щоб знайти точку перетину графіка з віссю , необхідно обчислити у при

х =0

у=

(0;-8) – точка перетину з віссю .

Відповідь: (-4; 0), (0; -8).

2. Графік  лінійної   функції  проходить через точку (-3;2). Знайти k.

Розв’язання. Щоб знайти к , підставимо замість точки х та у координати даної точки в рівняння, яким задана функція.

Точка (-3;2), то . Тоді

Відповідь:

3. Не виконуючи побудову графіків функцій та  , знайти координати точки їх перетину.

Розв’язання. Щоб знайти координати точки перетину графіків даних функцій, розв’яжемо рівняння:

Через те, що х=-3, то .

Точка перетину графіків (-3; -7).

Відповідь: (-3; -7).

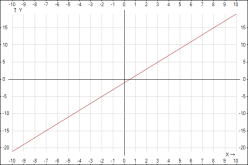
4. Побудувати графік функції . Це лінійна функція. Графіком є пряма. Для побудови прямої достатньо знати дві точки.

                 (0;-1), (2;3)                  

V. Підведення підсумків заняття.

VI. Домашнє завдання.

Повторити  §1 .

• Знайти нулі функції:

а) ;    б)

• Чи проходить графік функції:

а)   через точку (3;3);     б) через точку (2;2).