Тема заняття: Побудова графіків функцій за допомогою геомет­ричних перетворень .

Мета заняття: Формування умінь будувати графіки функцій за до­помогою восьми базових перетворень графіка функції у = f(x): у = -f(x);    у = f(-x); у = f(x) + b; у = f(x + a); у = af(x); у = f(ax); у = f(│x│);  у = │f(x)│.

Тип заняття: лекція комплексного характеру.

Обладнання: презентація «Перетворення графіків функції», таблиці.

Література: 1. Алгебра і початки аналізу. Підручник для 11 кл. загальноосвітніх навчальних закладів, М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчук. – К.: Зодіак – ЕКО, 2002, - 272 с.

 2. Алгебра і початки аналізу: Підручник для 10-11 кл. загальноосвітніх навчальних закладів. – К.: Освіта, 2006. – 255с.

План заняття

I. Організація початку заняття.

II.  Актуалізація опорних знань:

1) Перевірка домашнього завдання;

2) Розв’язування вправ аналогічних до домашніх.

III. Систематизація знань студентів

IV. Формування вмінь студентів будувати графіки.

V. Підведення підсумків заняття

VI. Домашнє завдання.

Хід заняття

I. Організація початку заняття.

II. Актуалізація опорних знань

1. Перевірка домашнього завдання.

2.     Розв'язування вправ, аналогічних до домашніх.

1) Знайдіть область визначення функції:

а) ;  б) .

Розв'язання

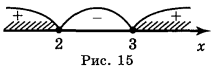
а) Через те що арифметичний квадратний корінь існує лише з не­від'ємних чисел, х² - 5х + 6 0 . Розв'яжемо нерівність методом інтервалів (знайдемо нулі функції g = х² - 5х + 6, нанесемо їх на координатну пряму і визначимо знак функції на кожному про­міжку) (рис. 1).

Отже, D(y) = (-; 2][3; +).

б) D(y) знаходимо розв'язавши систему 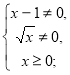.  Отже, D(y) = (0; 1)(1; +) 

2) Дослідіть на парність і непарність функцію:

а) f(x) = х²(2x - х³) ; б)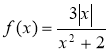

Розв'язання

а) Через те що D(f) = R і f(-x) = (-х)(2(-х) - (-х)³) = х²(-2х + х³) = -x²(2x - х³) = -f(x), f(x) = x²(2x –х³) — непарна.

б) Через те що D(f) = R і 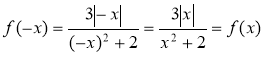 , то 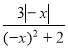– парна .

3) Чим відрізняються графіки функцій

y=x+3 і y=?

Розв'язання

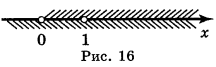
Праві частини даних рівностей тотожно рівні, оскільки . Але перший вираз має числові значення при всіх дійсних значеннях x, а другий – при всіх крім х=3. Тому графік першої функції – пряма, а другої  - пряма без однієї точки (рис. 3)

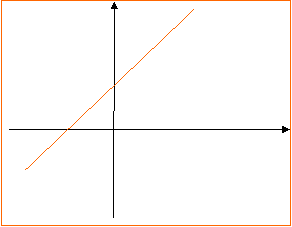
Рис. 3 

II. Повторення і систематизація знань студентів про геометричні перетворення графіків.

Запас функцій, графіки яких ви вмієте будувати, поки неве­ликий. Але використовуючи відомі із курсів геометрії і алгебри відомості про перетворення фігур, цей список можна суттєво розширити. Згадаємо елементарні перетворення графіка функції у = f(x) за допомогою таблиці 2. Щоб побудувати графіки складніших функцій, використовують такі правила:

• Графіки функцій y=f(x) і y= - f(x) симетричні відносно осі x.
• Щоб побудувати графік функції y=kf(x), де k>0, треба графік функції  y=f(x) розтягнути від осі х у k разів, якщо k>1, або стиснути його в 1/k разів до осі x, якщо 0<k<1.
• Щоб побудувати графік функції y=f (kx), де k>0, треба графік функції y=f(x) розтягнути від осі у в 1/k разів, якщо 0<k<1, або стиснути його в k разів, якщо k>1.
• Щоб одержати графік функції y=f(x)+п, треба графік функції y=f(x) перенести на п одиниць у напрямі осі у, якщо п>0, або на |п| одиниць у протилежному напрямі, якщо п<0.
• Щоб одержати графік функції у=f (x-m), досить графік функції y=f(x) перенести на m одиниць у напрямі осі x, якщо m>0, або на |m одиниць у протилежному напрямі, якщо m<0.

III. Формування умінь будувати графіки за допомогою геометричних перетворень відомих графіків.

Колективне виконання вправ

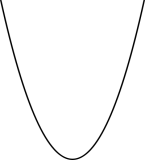
Побудувати графіки функцій а) ;

                                                  б)

IV. Підведення підсумків заняття.

1. Назвіть основні види функцій. Які їх графіки?

2. Що називають нулями функції?

3. Які функції називають зростаючими? А спадними?

4. Які функції називаються парними? Наведіть приклади парних функцій.

5. Які функції називаються непарними? Наведіть приклади непарних функцій.

V. Домашнє завдання.

Розділ І § 1 (3). Запитання і завдання для повторення № 27-31. Побудувати графік функції

І визначити, на якій множині значень аргументу дана функція спадає, а на якій зростає. При якому значенні х значення даної функції найменше?

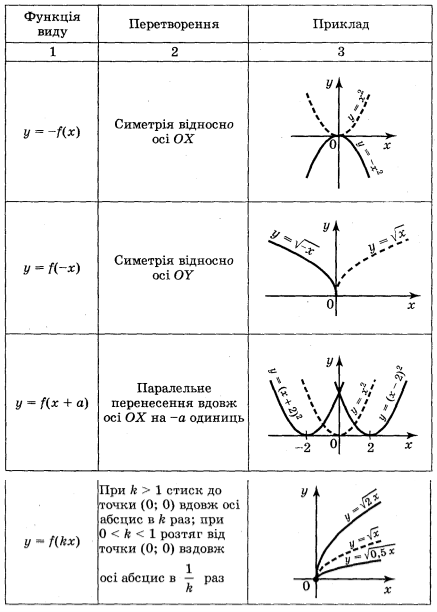
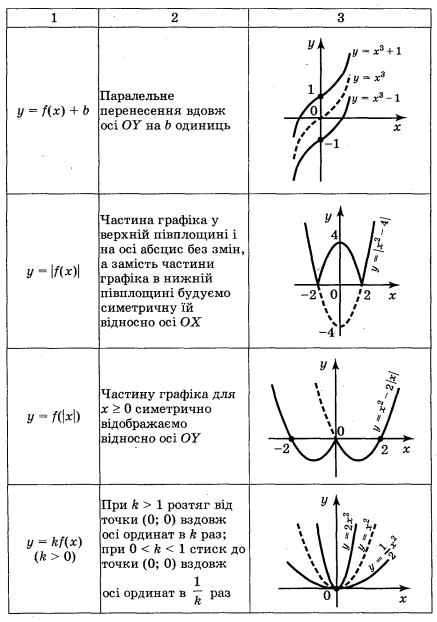Таблиця 2