Урок "Способи задання множин"

Урок 2

Тип урока: ОНЗ.

Тема: «Способы задания множества».

Основные цели:

1) формировать умение задавать множество перечислением и общим свойством элементов, познакомить с обозначением множеств;

2) повторить решение простых уравнений на умножение и деление, приемы устных вычислений, соотношение между единицами измерения длины, действия с именованными числами, анализ и решение текстовых задач.

Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, обобщение, классификация.

Демонстрационный материал:

1) картинки с изображением множеств (аналогичные № 1, стр. 4);

2) опорная схема по теме «Множество»:

 

 

 

3) таблица для этапа актуализации знаний:

 

 

 

 

4) карточки для 8 этапа:

 

 

 

 

 

 

 

 

 

 

 

6 · х = 42 20 : х = 5 х : 9 = 7

 

5) шаги плана выхода из затруднения:

1. Рассмотреть конкретные множества с их элементами;

2. Ответить на вопросы и проанализировать их;

3. Сделать вывод.

 

6) эталон способов задания множеств (из отдельных деталей):

СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ           А = {1, 2, 3,…9}                                                         А ― множество однозначных чисел Помни: Элементы множества не могут повторяться!

 

 

7) образец для самопроверки самостоятельной работы (этап 7):

 

 

 

 

8) таблица соотношений мер длины:

 

 

 

 

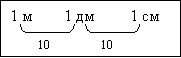
9) образец выполнения домашней работы:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Раздаточный материал:

1) пробное задание для этапа 2:

 

 

 

 

2) правила работы в группе:

 * В группе должен быть организатор обсуждения.

 * Каждый может высказать свою версию решения.

 * Один говорит, остальные слушают и пытаются понять.

 * Каждая версия обсуждается в группе.

 * В группе согласуется  общее решение.

 * Представитель группы защищает согласованное решение перед классом.

3) карточки с примерами множеств (для групповой работы);

а) заданного перечислением:            б) множество красных предметов

 

 

 

4) карточки для рефлексии (см. урок 1, М-3, ч-1).

 

Ход урока:

1. Мотивация к учебной деятельности.

Цель:

1) создать мотивацию к включению в деятельность на уроке;

2) организовать актуализацию требований к ученику со стороны учебной деятельности;

3) определить содержательные рамки урока: множества и их элементы.

Организация учебного процесса на этапе 1:

- С каким понятием вы познакомились на прошлом уроке? Покажите рисунки, которые вы сделали. Молодцы! Они вам сегодня понадобятся!

- Откройте тетради и проверьте по кодоскопу (Д-10), правильно ли вы решили дома задачу. Как найти, на сколько одно число больше или меньше другого?

- Кто решал уравнения? Как найти целое? Как найти часть? Проверьте ответы.

- А кто выбрал примеры на порядок действий? Сопоставьте свою запись с образцом.

- Как определить порядок действий в выражениях?

- Все увидели свои ошибки? Что с ними нужно сделать?

- А у кого все плюсы? Молодцы! Поставьте себе пятерки!

- Итак, что вы повторили на прошлом уроке? А что новое узнали?

- Как вы узнаёте новое? (Мы должны понять, что мы не знаем, а потом сами найдём способ для решения проблемы.)

- Сегодня вам предстоит вспомнить многое из того, что вы изучали во 2 классе ― площадь прямоугольника, решение уравнений на умножение и деление и др. И, конечно, вы продолжите работу с множествами. Так что у всех будет возможность заработать хорошие отметки! Я желаю вам успеха!

2. Актуализация знаний и фиксация затруднения в  пробном действии.

Цель:

1) актуализировать представления о множествах и их элементах, существенные свойства множеств;

2) тренировать мыслительные операции – анализ, сравнение, обобщение, классификацию – при повторении смысла арифметических действий,  приемов устных вычислений;

3) мотивировать к пробному действию; организовать его самостоятельное выполнение;

4) организовать анализ полученных ответов и зафиксировать индивидуальное затруднение.

Организация учебного процесса на этапе 2:

1) Актуализация представлений о множествах и их элементах.

- Давайте посмотрим, какие множества вы изобразили дома на своих рисунках.

Несколько детей показывают рисунки, остальные учащиеся определяют общее свойство нарисованных предметов и называют их, используя понятие множества: например, множество деревьев, множество рыб и т.д.

Учитель показывает картинки, аналогичные № 1, стр. 4 (Д–1) (можно работать по учебнику) и опорную схему Д–2.

- Объясните понятие: «множество» предметов? (Предметы собраны вместе, ни один из них не повторяется.)

- Назовите свойство, которое объединяет все элементы данных множеств. (а ― параллелепипеды, б ― оранжевые предметы, в ― цилиндры, г ― стеклянные предметы, д ― инструменты, е ― одежда.)

- Назовите 3 элемента множества грибов.

- Является ли элементом этого множества подберезовик? (Да.)

- Принадлежит ли этому множеству ежик? (Нет.)

2) Уточнение смысла арифметических действий.

На доске выставляется карточка Д–1 (1).

- Как можно назвать множество записей на доске? (Это множество выражений.)

2 + 12 + 4, 12 : 4, 12 – 2, 4 + 2, 12 : (4 + 2)?

- Веселый маленький ежик нес на своей колючей спинке 2 яблока. В лесу он нашел 12 шишек и 4 грибка. Что означают эти выражения?

3) Тренинг мыслительных операций.

- Вычислите устно, записывая только полученные результаты:

• Делимое 56, делитель 7. Найдите частное.
• Уменьшите 160 в 10 раз.
• Найдите произведение чисел 6 и 4. 
• На сколько 8 меньше 40?
• Я задумала число, уменьшила его в 2 раза, получила 20. Какое я число задумала?

(8, 16, 24, 32, 40.)

- Что интересного в полученном ряду чисел? (Числа увеличиваются на 8.)

- Продолжите ряд, чтобы эта закономерность сохранялась. (48, 56, 64, 72 …)

- Есть ли у данного множества самое большое число? (Нет, 8 можно присчитывать сколько угодно раз.)

- О таком множестве говорят, что оно бесконечно. А можно ли отнести к этому множеству число 17? (Нет, оно не делится на 8.) Число 80? (Да, оно делится на 8.) Мотоцикл? (Нет ― это вообще не число.)

- Что вы сейчас повторили? (Понятия «множество», «элемент множества» …)

- Как вы думаете, что я вам сейчас предложу и зачем? (Вы нам предложите задание, которое мы никогда не делали, для того что бы мы поняли чего мы её не знаем. Мы попробуем с ним справится.)

4) Задание для пробного действия.

- Вы отлично справились с определением того, является объект элементом множества или нет. А теперь пробное задание.

Учитель раздает на листках задание Р–1. Учащиеся должны индивидуально ответить на вопрос, является ли число 98 элементом множества больших чисел.

При выполнении данного задания возникает затруднение ― некоторые дети дадут положительный ответ на вопрос, другие ― отрицательный, кто-то не даст никакого ответа ― сообразит, что ответить на данный вопрос невозможно. Возникшее затруднение фиксируется:

1.- Кто ничего не написал, в чём затруднение? (Я не смог определить является ли число 98 элементом множества больших чисел или нет.)

2.- Кто ответил «да»? Кто ответил – «нет»?

- Вы можете обосновать свой ответ на вопрос, каким способом? (Мы не можем обосновать, у нас нет такого способа.)

3. Выявление места и причины затруднения.

Цель:

1) организовать восстановление выполненных операций;

2) организовать фиксацию места (шага, операции), где возникло затруднение;

3) организовать соотнесение своих действий с используемыми эталонами (алгоритмом, понятием и т.д.).

На этой основе организовать выявление и фиксацию во внешней речи причины затруднения – тех конкретных знаний, умений или способностей, которых недостает для решения исходной задачи и задач такого класса или типа вообще.

Организация учебного процесса на этапе 3:

- Стоп! Уточните еще раз, на какой вопрос вам нужно ответить? (Принадлежит число 98 множеству больших чисел, или нет.)

- Где возникло затруднение? (При выборе ответа.)

- А почему вы не смогли это определить? Ведь только что было такое же задание! (Там было указано свойство элементов множества – числа, кратные 8.)

- Здесь тоже сказано – большие числа! (Но мы не знаем, какие числа считать большими!)

- Молодцы! Вы верно подметили разницу в этих заданиях.

 

4. Построение проекта выхода из затруднения .

Цель:

Организовать построение проекта выхода из затруднения:

1) учащиеся ставят цель проекта: построить способ изображать часть множества;

2) учащиеся уточняют и согласовывают тему урока;

3) учащиеся определяют средства (алгоритмы, модели, справочники и т.д.).

4) учащиеся формулируют шаги, которые необходимо сделать для реализации поставленной цели.

Организация учебного процесса на этапе4:

- В математике говорят, что множество задано, если про каждый предмет можно точно сказать, принадлежит он данному множеству, или нет. Множество кратных 8 ― задано, а второе множество ― нет. Как вы считаете, важно уметь правильно задавать множества? (...)

- Очень важно! Представляете, как бы мы работали, если бы сами не знали, кто учится в нашем классе, а кто ― нет! Значит, чему вы должны научиться? (Правильно задавать множества.) (Цель.)

- Верно! Тема урока: «Способы задания множества». - открывается на доске.

- Что вам может помочь в достижении цели? (Понятие множества, элементы множества.)

- Давайте составим план преодоления затруднения:

1) Рассмотреть несколько множеств с их элементами.

2) Ответить на вопросы и проанализируем ответы.

3) Сделаем вывод.

 

5 . Реализация построенного  проект.

Цель:

1) организовать коммуникативное взаимодействие с целью реализации построенного проекта, направленного на приобретение недостающих знаний;

2) организовать согласование способов и фиксацию построенного способа действия в речи и знаково (с помощью эталона);

3) организовать уточнение общего характера нового знания.

Организация учебного процесса на этапе 5:

Рассматривается два «удобных» примера множеств, которые придумали дети. Например, множество красных предметов и множество{5, берёза, грузовик}. Организовать работы можно в группах, необходимо вспомнить правила работы в группах.

Задание группам:

1 , 3 группы: множество красных предметов

Вопросы:

1) перечислите несколько элементов множества;

2) принадлежит ли этому множеству ворона, огурец, 98, красный помидор?

3) как вы это определили?

4) про любой предмет можем сказать: принадлежит он этому множеству или нет?

5) значит множество задано - верно?

6) каким способом задано множество?

7) вывод.

2, 4 группы: множество{5, берёза, грузовик}.

Вопросы:

1) назовите элементы данного множества;

2) принадлежит этому множеству число 9? Трамвай? Береза?

3) про любой предмет можно точно ответить на этот вопрос?

4) сделайте вывод;

5) есть ли у элементов этого множества общее свойство?

6) а как же оно задано?

7) как бы вы назвали этот способ задания множества?

8) вывод.

Представители групп у доски обобщают свою групповую работу, при этом уточняется, что элементы перечисляются в фигурных скобках и при перечислении элементы не могут повторяться. На доске появляется «собранный» эталон Д–4, фиксирующий оба способа задания множеств.

- Проверим по учебнику, правильно ли вы рассуждали. Прочитайте текст в рамке на стр. 5 и подчеркните ответы на вопросы:

1) Когда множество задано? (Если о любом предмете  можно точно сказать, является ли он элементом этого множества.)

2) Какими способами можно задать множество? (Перечислением его элементов или общим свойством его элементов.)

- Каким способом вы зададите бесконечное множество и почему? (Общим свойством его элементов, перечислить такое множество будет невозможно.)

- Приведите пример бесконечного множества. (Множество чисел, оканчивающихся нулем; множество натуральных чисел, множество чисел содержащих цифру 7 и т.д.)

- Каким способом вы зададите конечное множество и почему? (Общим свойством его элементов или перечислением  элементов множества. Множество, которое имеет конец можно задать любым способом.)

- Приведите пример конечного множества и задайте его двумя способами. (Множество предметов прямоугольной формы на картинке (№1 стр.4)   – телевизор, книга, коробка, шкаф, дом и т.д.)

В завершение, обсуждается задание, вызвавшее затруднение.

- Когда множество задается свойством, его надо указывать правильно, или корректно, чтобы о каждом предмете можно было точно сказать, обладает он этим свойством или нет. Почему нельзя указать свойство ― «большое число»? (Мы не договорились, какие числа отнести к большим, а какие ― к маленьким.)

- Уточните эту формулировку. Какие числа вы бы предложили назвать «большими»? (Например, те, которые больше 1000.)

- Тогда как вы ответите на поставленный вопрос? (Число 98 этому множеству не принадлежит? Докажите. (98 < 1000.)

- Решили вы свою задачу? (Да.) Молодцы!

 

6. Первичное закрепление во внешней речи.

Цель:

создать условия для фиксации изученного способа действий во внешней речи.

Организация учебного процесса на этапе 6:

Задания выполняются с комментированием способов действий в громкой речи. Перед выполнением заданий учитель уточняет, что множества принято обозначать большой латинской буквой, а его элементы записываются в фигурных скобках.

1) Фронтальная работа: № 3–5, 6 (а, б), 7 (а), стр. 5–6.

- Рассмотрите иллюстрацию. Кто помнит, что сдавала дама в багаж из стихотворения Маршака. (Диван, чемодан, саквояж, картину, корзину, картонку и маленькую собачонку.)

- Каким способом задано множество предметов багажа? (Перечислением – все предметы просто названы.)

- Принадлежит ли этому множеству стол? (Нет.) Докажите. (Его нет среди перечисленных предметов.)

Если позволит время, можно перечислить элементы 2–3 множеств из № 4–5, стр. 5.

№ 6 (а ,б), стр. 6

а) В списке перечислены все однозначные числа. Это их общее свойство. Значит, А ― это множество цифр;

б) В ― множество однозначных четных чисел.

№ 7 (а), стр. 6

{к, р, о, т}.

2) Работа в парах: № 7 (в, г), стр. 6 (проверку провести фронтально)

№ 7 (в, г), стр. 6

в) {10, 20, 30, 40, 50, 60, 70, 80, 90}; г) {604, 605, 606, 607}.

7 . Самостоятельная работа с самопроверкой  по эталону.

Цель:

1) организовать самопроверку и самооценку учащимися умения  задавать множества разными способами.

 

Организация учебного процесса на этапе 7:

- Теперь я предлагаю вам самостоятельно выполнить № 6 (в), стр. 5 и № 7 (б), стр. 6. Успешной вам работы!

Учащиеся работают самостоятельно. На самостоятельную работу отводится 1–2 минуты.

- Закончили работу.

Учитель помещает на доску образец для самопроверки Д–8 и эталон Д–6.

- Проверьте себя по образцу и эталону, зафиксируйте результат проверки при помощи знаков «+» или «?».

Дети выполняют самопроверку и фиксируют ее результат.

- Какие возникли затруднения? (Перепутал знаки; забыл перечеркнуть знак «принадлежит»; не понял задание…)

- Исправьте ошибки.

- Поднимите руки те, кто сделал все верно? (…) Молодцы!

 

8. Включение в систему знаний и повторение.

Цель:

1) повторить решение простых уравнений на умножение и деление, приемы устных вычислений, соотношение между единицами измерения длины, действия с именованными числами;

2) тренировать способность к анализу и решению текстовых задач.

Организация учебного процесса на этапе 8:

1) Повторение формулы площади прямоугольника и ассоциативного способа решения простых уравнений на умножение и деление.

Учитель выставляет на доске карточки Д–2 (2, 3).

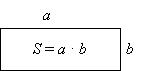
- Чему равна площадь прямоугольника со сторонами a и b? (Произведению длин сторон a и b.)

 

 

 

 

- У ежика есть прямоугольный участок земли, стороны которого равны 4 м и 9 м. Какова площадь участка? (9 · 4 = 36 квадратных метров.)

- Как найти сторону прямоугольника, если известна площадь и другая сторона? (Площадь разделить на длину известной стороны.)

- Решите уравнения, пользуясь рисунками. (х = 7, х = 4, х = 63)

 

 

 

 

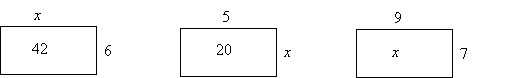
6 · х = 42 20 : х = 5 х : 9 = 7

- Как в уравнениях найти неизвестный множитель, делитель, делимое?

 

2) Решение уравнений: № 9, стр. 6.

- Теперь займемся повторением. Какой моделью мы пользуемся при решении уравнений на умножение и деление? (Прямоугольником.)

- Посмотрите на уравнения в № 9. Мысленно представьте прямоугольник и определите, в каких уравнениях неизвестна сторона. (В первом и третьем.)

- Каким действием находим сторону? (Делением.)

- Какое действие выберете при решении второго уравнения? (Умножение.) Почему? (Ищем площадь.)

Работа организуется в группах. Каждая группа в течение 2 мин решает по одному уравнению. Трое учащихся в разных группах работают с переносной доской, остальные ― в тетрадях. Затем те, кто работал на переносных досках, озвучивают решение своих уравнений с комментированием по компонентам действий, а остальные дети проверяют и записывают в тетрадях решение уравнений других групп. Попутно обсуждаются приемы умножения и деления круглых чисел, внетабличного умножения и деления. 

Ответы: х = 8,   х = 294,   х = 2. 

3) Действия с именованными числами:  № 11, стр. 6.

- Что надо вспомнить перед выполнением этого задания? (Соотношение мер длины.)

Выставляется таблица Д–7:

 

 

 

 

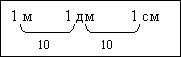
- Сколько дециметров в 1 м, сантиметров в 1 дм, сантиметров в 1 м?

- С чего начнете решение? (Выразим числа в одинаковых единицах измерения.)

Первые три примера распределяются по одному в группу. Работа организуется так же, как и при решении уравнений.

Запись:  3 м 7 дм 6 см + 4 м 3 дм 8 см = 376 см + 438 см = 814 см = 8 м 1 дм 4 см

                     1 1

          3 7 6

          4 3 8

          8 1 4

Ответы: 8 м 1 дм 4 см,   6 м 4 дм 1 см,   9 м 1 дм 3 см.

 

4) Приемы устного сложения и вычитания чисел:  № 8, стр. 6.

Задание выполняется в форме игры: «Кто быстрее?», выполняется на печатной основе. Обратить внимание на вычислительный приём: 85 – 39=85 – 40 + 1.

5) Анализ и решение задачи: № 10, стр. 6.

В начале этапа учитель вызывает одного ученика для работы по задаче № 10, стр. 6. На доске нарисована заготовка для схемы. Он параллельно работе групп «одевает» схему, составляет план решения задачи и готовит ее для ответа. В завершение урока он проводит анализ задачи.

 

 

 

 

Анализ задачи:

– В первый день Ира прочитала 21 страницу, во второй ― в 2 раза больше, чем в первый, а в третий ― на 15 страниц меньше, чем во второй. Надо узнать, сколько страниц она прочитала за все три дня вместе.

Чтобы ответить на этот вопрос, надо сложить количество страниц, которые Ира прочитала за каждый из трех дней. (Ищем целое.) Но вначале надо найти, сколько она прочитала за второй и третий дни. Для этого вначале умножим 21 на 2 ― узнаем количество страниц во второй день, а потом из полученного числа вычтем 15.

План решения задачи можно записать в виде схемы:

 

II   →   III  →   I + II + III

9. Рефлексия учебной деятельности на уроке.

Цель:

1) зафиксировать новое содержание, изученное на уроке;

2) оценить собственную деятельность и работу класса в целом;

3) зафиксировать неразрешенные затруднения, если они есть, как направления будущей учебной деятельности;

4) обсудить и записать домашнее задание.

Организация учебного процесса на этапе 9:

- Какую цель мы ставили перед собой сегодня ? Достигли вы цели ? Докажите.

- Что нового узнали?

- Когда можно сказать, что множество задано?

- Какими способами можно задать множество?

- Что вы сегодня повторили?

- В чем было затруднение? Над чем еще надо поработать?

- Какие группы сегодня слаженно работали? Кого из ребят вы отметите?

- Оцените свою работу. (детям даются (проговариваются) критерии оценивания своей

деятельности из предыдущего урока)

 

Домашнее задание:

  повторить таблицу умножения, взаимозачет ― в парах;

 № 10 – построить схему и записать решение; № 11 (4), № 12;

☺ придумать множество, которое можно задать двумя разными способами.

            – Каким оно должно быть? (Конечным и элементы должны обладать
                       общим свойством.)