Урок " Стандартні графічні процедури і функції для роботи з координатами, вікнами"

Стандартні графічні процедури і функції для роботи з координатами, вікнами.

Для побудови зображення у графічному режимі використовують систему координат, яка відрізняється від текстового режиму (екран представляється у вигляді прямокутного масиву символів і координати Х, Y починаються з 1 … max значення).

Відлік координат починається з верхнього лівого кута екрана з координатами (0, 0). При цьому екран представляється у вигляді прямокутного масиву адресованих точок (пікселів). Для різних типів адаптерів та режимів кількість точок по вертикалі та горизонталі суттєво відрізняється.

Для визначення максимальних значень координат екрану, в модулі GRAPH використовують функції:

GetMaxX: integer; GetMaxY: integer.

Особливості: якщо при адресації точок вказуються значення координат, які перевищують максимальні, то операція ігнорується.

Спосіб побудови зображень з використанням абсолютних координат не завжди є зручним, оскільки виникають випадки, коли необхідно змінювати розташування, чи розміри зображень.

При використанні абсолютних координат це є  неможливим, принаймні для швидкого коригування програм, що є дуже незручним. Також даний метод є дещо незручним при побудові зображень із симетричними об’єктами.

В такому випадку використовують метод відносних координат – метод, коли координати графічних елементів задаються не відносно початку координат екрану, а відносно змінних, яким задаються певні значення координат перед початком побудови. При використанні даного методу, переміщення графічних об’єктів зводиться до зміни значень лише двох координат. У випадку масштабування вводяться додаткові змінні – коефіцієнти, які множаться на значення координат.

Зобразимо систему відносних координат. Початок машинної системи координат, напрямок осей, а також максимальні значення координат монітора показані на рисунку.

 На рисунку представлено також машинну (xm, ym) та фізичну (відносну - x, y) системи координат. Для зображення на екрані точки з фізичними координатами (x, y) необхідно визначити її машинні координати (xm, ym). Розрахункові формули мають наступний вигляд: x_m=x₀+x*M_x, y_m=y₀-y*M_y,

де Mx, My-масштаби відповідно по осях x і y, які показують кількість пікселів в одній фізичній одиниці, x, y- фізичні координати точки, xm, ym- машинні координати точки, x0, y0- машинні координати початку фізичної системи координат.

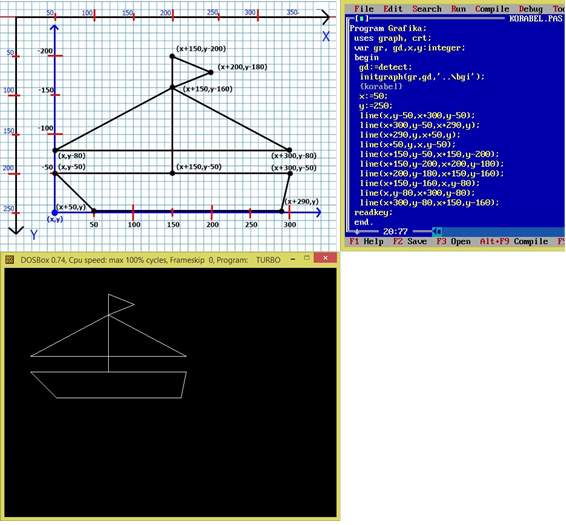
Така система використовується скоріше для побудови складних об’єктів (таких що мають багато елементів), наприклад побудова корабля, автомобіля, тощо.

Приклад: Намалювати корабель, використовуючи відносну систему координат.

При побудові зображень із симетричними елементами використовую умовні осі симетрії, проведені через середину рисунка. Зазвичай такі побудови виконуються відносно центру екрану. Відомо, що у графічному режимі Pascal координати центру рівні (319,239), проте не завжди можна згадати ці числа. Їх можна визначити за допомогою нескладних розрахунків – максимальні значення координат (функції GetMaxX та GetMaxY) – розділивши націло на 2:

координати центру екрану:

xс:= GetMaxX div 2;

yс:= GetMaxY div 2;

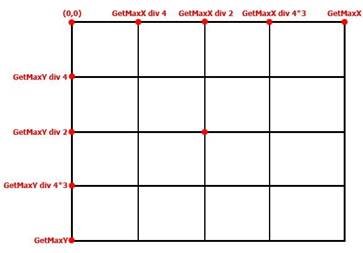
На рисунку представлено розподіл координат         екрану            через   розділ їх максимальних            значень.          Наприклад, координати центру можна представити як (GetMaxX div 2, GetMaxY div 2), ліва нижня четверть – (GetMaxX div 4, GetMaxY div 4*3), права половина        – (GetMaxX    div       4*3,

GetMaxY div 2), тощо.

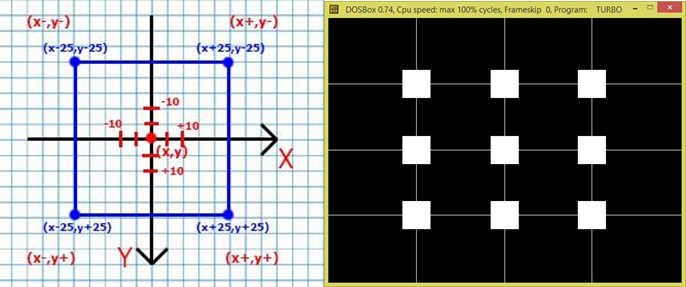
Приклад: Написати програму, яка виконує наступні дії:

1.      будує на екрані сітку з трьох горизонтальних ліній і трьох вертикальних, які перетинаються в центрі, серединах і четвертях;

2.      побудувати зафарбовані квадрати в 9-ти точках, де перетинаються прямі. Для побудови використати відносні координати.

Для спрощення і зрозумілості коду, на початку побудови, для змінних x та y присвоїмо відповідні максимальні значення координат.

Для побудови квадратів використовуватимемо відносні системи координат, центрами яких будуть точки перетину ліній. Дані системи мають вигляд перевернутих Декартових систем координат.

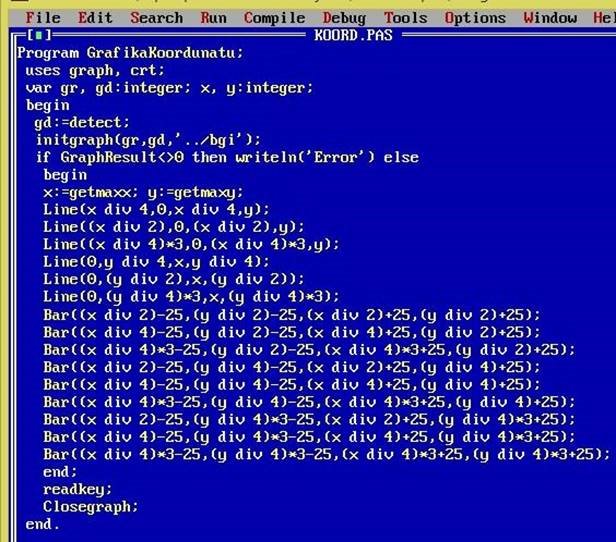
Program GrafikaKoordunatu;  uses graph, crt;  var gr, gd:integer; x, y:integer; begin   gd:=detect;   initgraph(gr,gd,'../bgi'); if graphrezult<>0 then writeln(‘Error’) else begin

   x:=getmaxx; y:=getmaxy;

   Line(x div 4,0,x div 4,y);

   Line((x div 2),0,(x div 2),y);

   Line((x div 4)*3,0,(x div 4)*3,y);

   Line(0,y div 4,x,y div 4);

   Line(0,(y div 2),x,(y div 2));

   Line(0,(y div 4)*3,x,(y div 4)*3);

   Bar((x div 2)-25,(y div 2)-25,(x div 2)+25,(y div 2)+25);

   Bar((x div 4)-25,(y div 2)-25,(x div 4)+25,(y div 2)+25);

   Bar((x div 4)*3-25,(y div 2)-25,(x div 4)*3+25,(y div 2)+25);

   Bar((x div 2)-25,(y div 4)-25,(x div 2)+25,(y div 4)+25);

   Bar((x div 4)-25,(y div 4)-25,(x div 4)+25,(y div 4)+25);

   Bar((x div 4)*3-25,(y div 4)-25,(x div 4)*3+25,(y div 4)+25);

   Bar((x div 2)-25,(y div 4)*3-25,(x div 2)+25,(y div 4)*3+25);

   Bar((x div 4)-25,(y div 4)*3-25,(x div 4)+25,(y div 4)*3+25);

Bar((x div 4)*3-25,(y div 4)*3-25,(x div 4)*3+25,(y div 4)*3+25);   End; readkey;    Closegraph;  end.