Урок «Сума кутів трикутника».

Про матеріал

Автор розробки пропонує організувати засвоєння знань про суму кутів трикутника у вигляді уроку-кейсу. Розв'язувати задачі практичного змісту доводиться чи не кожному з нас майже щодня. Деякі з них розглядаються на цьому уроці.

Перегляд файлу

Урок математики у 7-му класі

Алла МОРОЗОВА, вчитель математики Смілянської спеціалізованої школи І-ІІІ ст. № 12, Черкаська обл.

Автор розробки пропонує організувати засвоєння знань про суму кутів трикутника у вигляді уроку-кейсу. Розв’язувати задачі практичного змісту доводиться чи не кожному з нас майже щодня. Деякі з них розглядаються на цьому уроці.

Тема уроку. «Сума кутів трикутника».

Мета уроку:

Навчальна:

створити умови для сприйняття, осмислення і первинного закріплення блоку нової навчальної інформації по темі «Сума кутів трикутника».

формувати практичні навички застосування знань про властивості трикутника при розв’язуванні завдань з життєвим навантаженням;
узагальнити знання про трикутник, вивчити, осмислити і вміти застосовувати теорему про суму кутів трикутника, розширити знання про різновиди трикутників.
підвищити мотивацію до вивчення теми «Сума кутів трикутника»;
знати теорему про суму кутів трикутника, вміти застосовувати її під час вирішення завдань, свідомо обирати найбільш ефективні шляхи вирішення, розвивати вміння працювати з навчальним текстом, проводити класифікацію трикутників в залежності від їх кутів.
усвідомити цінність знань для повсякденного життя;
формувати ключові, предметні і міжпредметні компетентності.

Розвивальна:

розвивати логічне мислення, монологічне і діалогічне математичне мовлення, аналітичні уміння і навички (класифікувати, аналізувати, мислити чітко, генерувати альтернативні рішення, переконувати).

Виховна:

виховувати: працьовитість, креативність, ініціативність, активність, вольові якості, цілеспрямованість, впевненість в собі, конкурентоспроможність, самостійність у прийнятті рішень в умовах невизначеності.

Ключові компетентності, які формуються на уроці

Ціннісно-смислові:

формулювати свої ціннісні орієнтири по відношенню до навчального предмету та сфери діяльності, володіти способами самовизначення в ситуації вибору на основі власних позицій;
уміти приймати рішення, брати на себе відповідальність за наслідки, здійснювати дії та вчинки на основі обраних цільових установ.

Навчально-пізнавальні:

ставити мету і організовувати її досягнення, уміти пояснити мету;
організовувати планування, аналіз, рефлексію, самооцінку своєї пізнавальної діяльності;
ставити пізнавальні задачі і знаходити їх розв’язання;
володіти вимірювальними навичками, працювати з інструментами, діловими паперами;
описувати результати, формулювати висновки; розповідати усно чи письмово про результати свого дослідження з використанням мультимедійних засобів.

Соціокультурні:

володіти знаннями і досвідом виконання соціальних ролей працівника, власника; уміти діяти в щоденних ситуаціях сімейно-побутової сфери;

Комунікативні:

володіти способами взаємодії; уміти задавати питання, коректно вести навчальний діалог;
володіти різними способами діяльності в групі; прийомами дії в ситуаціях спілкування, умінням шукати і знаходити компроміси.

Інформаційні:

володіти навичками роботи з різними джерелами інформації: словником, довідниками; Інтернет-ресурсами;
самостійно шукати, систематизувати, аналізувати і відбирати необхідну інформацію для вирішення навчальної задачі;
орієнтуватись в інформаційному просторі, усвідомлено сприймати інформацію;
володіти навичками роботи з комп’ютером, телефоном.

Здоров’язберігаючі:

володіти способами емоційної саморегуляції, підтримки і самоконтролю.

Тип уроку. Урок когнітивного типу; урок постановки проблем і їх рішень за Case - технологією з використанням методів аналізу – методу ситуативного аналізу (Case-study) .

Вид кейсу. Навчальний.

Обладнання: мультимедійний проектор, кейси учнів, висловлювання видатних людей про математику.

Тривалість: 1 академічна година

Хід уроку
1.Організаційний момент

Вчитель перевіряє готовність учнів до уроку. Створює позитивний емоційний настрій, включає учнів в діяльність.
2. Цілепокладання і мотивація.
Мотивує учнів, подводить їх до формулювання теми і цілей уроку. Створює проблемну ситуацію.
3. Актуалізація знань учнів.
Пропонує учням фронтальну роботу з повторення вивченого матеріалу, необхідного для «Відкриття нових знань».
4. Первинне засвоєння нових знань
- Пропонує розбитися на групи по 4 учні і побувати в ролі дослідників, виконавши дослідницьку роботу.

1 група - завдання на перегинання трикутників.

2 група - завдання на розрізування трикутників.

3 група - вимірювання кутів трикутників транспортиром.
- Організовує і спрямовує діяльність учнів в парах по оригінальному пошуку доведення теореми.
5. Первинна перевірка розуміння вивченого матеріалу.
- За допомогою питань підводить учнів до класифікації трикутників в залежності від їх кутів. Привертає учнів на самостійний пошук інформації за підручником, організовує роботу в парах.
6.Закріплення навчального матеріалу

7. Рефлексія навчальної діяльності на уроці.

(Підсумок уроку)
8. Інформація про домашнє завдання.
1. Вступне слово вчителя.

Перш ніж приступити до роботи, згадаємо, що вивчає наука геометрія? Учні: геометрія-це наука про властивості геометричних фігур

Вивченню якої фігури ми приділяємо найбільше уваги в 7 класі? Як ви думаєте, чому саме з трикутника ми починаємо вивчати геометрію? Трикутник найпростіша замкнута геометрична фігура, властивості якої людина дізналася ще в глибоку давнину, так як ця фігура жорстка, має широке застосування в практичному житті при будівництві будинків, мостів та інших споруд.

Учні відповідають на питання, відповіді на які повинні були підготувати вдома:

1) У назві якого географічного об’єкту зустрічається назва трикутника?

(Бермудський)

2) Які материки схожі формою на трикутник? (Африка і Південна Америка)

3) Які корисні копалини позначаються трикутником? (нафта, природний газ, залізна руда)

4) Один з найбільших островів схожих на трикутник? (Гренландія)

2. Демонстрація малюнків-прикладів трикутників.

Перший учень : «Геометричні фігури ми можемо спостерігати скрізь і навіть у мистецтві» (і наводить приклади на малюнках).

Другий учень : «Проходять століття, але роль геометрії в архітектурі не зменшилася. Вона як і раніше залишається її «граматикою». У наш час нових технологій архітектура творить нестандартні архітектурні форми, пов’язані з трикутником». (Демонструю малюнки).

$C:\Users\Надежда\Downloads\i (1).jpg$ $C:\Users\Надежда\Downloads\i (2).jpg$ $C:\Users\Надежда\Downloads\i (5).jpg$

$C:\Users\Надежда\Downloads\рабочий стол.jpg$ $C:\Users\Надежда\Downloads\i (3) - копия.jpg$ $C:\Users\Надежда\Downloads\i (4).jpg$

Використання рівностороннього трикутника нашими предками

У стародавньому мистецтві дуже широко поширюються зображення рівностороннього трикутника . Первісні люди штампували трикутники на різних виробах.
Вожді племен північно-американських індійців носили на грудях символ влади — рівносторонній трикутник з крапкою в центрі
В Африці жінки також прикрашають себе великими пластинами рівносторонніх трикутників.
Рівносторонні трикутники малювали – на зображеннях священних тварин.

Хоч трикутник і найпростіший з вигляду багатокутник, але за кількістю властивостей він випереджає багато інших геометричних фігур.

З трикутниками ми зустрічаємось досить часто : вітрило корабля, повітряний змій, дах будинку і т. д. – все це трикутники. Мабуть, це найголовніша фігура, бо з трикутників, як з цеглинок, складаються майже всі геометричні фігури, які ми будемо вивчати далі.

3. Актуалізація опорних знань.
А зараз ми повторимо ті геометричні фігури, які ми вивчали раніше і які нам знадобляться при вивченні даної теми уроку.

Гра «Відгадайка»

Один учень класу виходить до дошки і встає спиною до екрану.

На екрані з'являються такі фігури:

• Пряма

• Промінь

• Кут

• Точка

Учні класу описують ту фігуру, яку вони бачать на екрані, кажуть її визначення, а учень відгадує, що зображено на екрані.

Вчитель опитує методом «незакінченого речення»

1) Трикутником називається…( геометрична фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, що сполучають ці точки)

2) Дві геометричні фігури називаються рівними, якщо…(вони суміщаються при накладанні)

3) Якщо сторона і два прилеглі до неї кути…( одного трикутника дорівнюють відповідно стороні й прилеглим до неї кутам другого трикутника, то такі трикутники рівні)

4) Рівнобедреним називається трикутник…( у якого дві сторони рівні.)

5) Різностороннім називається трикутник…( у якого всі сторони мають різну довжину)

6) Якщо у трикутника всі кути рівні…( то він рівносторонній)

7) Медіаною трикутника називається…( відрізок, що з'єднує вершину трикутника із серединою протилежної сторони)

8) Бісектриса в рівнобедреному трикутнику є …(медіаною і бісектрисою)

11) Кожний кут має …(свою градусну міру)

12) Дві прямі, які не перетинаються …(паралельні)

13) Твердження, яке доводиться …(аксіома)

14) Якщо одна сторона спільна, а дві інші доповняльні …(суміжні кути)

15) Кут суміжний з прямим …(прямий)

16) Вертикальні кути завжди …(рівні)

17) Гострий кут – це…(кут менше 90˚)

18) Якщо прямі перетинаються під прямим кутом…(перпендикулярні)

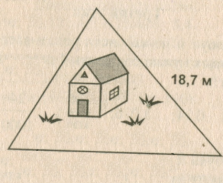Завдання . Завдання кота Базіліо для лисиці Аліси.

Лисиця Аліса: «Я виміряла усі сторони своєї трикутної ділянки. Довжина кожної сторони по 18,7 м. Мій сусід кіт Базіліо сказав, якщо я знайду периметр своєї ділянки, він зможе посадити кущі троянд.Але я не можу цього зробити, бо я незнаю такого дивного слова «периметр»».

Діти допоможемо знайти лисиці Алісі периметр своєї ділянки.

Розв’язання: (периметр рівностороннього трикутника)

4. Групова робота. Клас розділяється на три групи. Кожна група отримує задачі, над розв’язанням яких міркує вся група з наступним розв’язанням їх на дошці одним із учасників групи, решта учнів записують розв’язання у зошиті.

Рисунок 1

Зміст інформаційного Кейсу

Трикутник
1. Означення. Елементи
	∆АВС: А, В, С — вершини; АВ, ВС, АС — сторони; A, B, C — кути
2. Периметр трикутника
Р = АВ + ВС + АС
3. Види трикутників (за кутами)
гострокутний	прямокутний		тупокутний
4. Нерівність трикутника
		\|b – c\| < a < b + c

Зміст практичного кейсу 1

Група перша.

Який трикутник треба взяти, щоб після проведення в ньому одного відрізка отримати такі види трикутників: рівнобедрений, різносторонній, прямокутний, гострокутний?

Група друга

Як провести одну лінію в довільному трикутнику, щоб розділити його на чотири фігури?

Третя група

Довжина однієї сторони трикутника 6,31м, другої – 0,82м. Яка довжина третьої сторони, якщо відомо , що вона складає ціле число метрів?

Презентація групи 1

Якщо в прямокутному трикутнику з гострим кутом 45° проведемо медіану із вершини прямого кута, то отримаємо такі види трикутників: рівнобедрений, різносторонній, прямокутний, гострокутний.

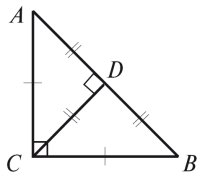
36-3 Рисунок

Презентація групи 2

Щоб розділити трикутник на чотири фігури потрібно вписати коло в довільний трикутник.

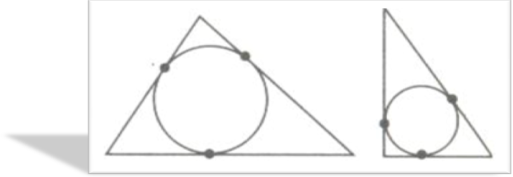
ЗОБР 016

Презентація групи 3

Ми скористалися нерівностями трикутника:

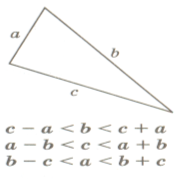
Отже, якщо довжина однієї сторони трикутника 6,31м, другої – 0,82м, то довжина третьої сторони 6 м або 7м.

Учитель: Зараз я хочу запропонувати вам виступити в ролі дослідників і зробити математичне обґрунтування своїх спостережень і припущень. Може бути, у вас і не вийде зробити ніяких нових відкриттів в області геометрії, але кожен з вас побуває в ролі першовідкривача, якщо буде уважним і спостережливим.

Чертех

Завдання групам: шляхом дослідження висунути гіпотезу про суму кутів трикутника.
Проблемна ситуація (завдання нездійсненне взагалі):

Побудуйте трикутник з кутами 100˚, 200˚, 60˚.

Учитель: - Ви можете накреслити такий трикутник? (Спонукання до усвідомлення протиріччя.)

Учні: - Ні, не виходить! (Усвідомлення труднощів.)

Учитель: - Який же питання виникає? (Спонукання до формулювання проблеми.) Учні: - Чому не будується трикутник? (Проблема як питання, яке не збігаєтьсяз темою уроку.)
Формулювання навчальної проблеми. Діалог, що спонукає до висування і перевірки гіпотези.

Зміст практичного кейсу 2

Група перша.

- Будуйте трикутник з двома прямими кутами.

Група друга

- Будуйте трикутник з двома тупими кутами.

Третя група

- Будуйте трикутник з тупим і прямим кутом.

Учні: - Ні, не виходить!

Вчитель: Що ж можна припустити про суму кутів трикутника?

Зміст практичного кейсу 3

Завдання 1 групі: учням видаються паперові моделі трикутників. Шляхом перегинання отримати прямокутник і зробити висновок про суму кутів трикутника.
Завдання 2 групі. На парті три трикутника різних видів гострокутий, прямокутний, тупокутний. Розрізати трикутники на три частини, щоб вийшло три кути. Спробувати визначити їх суму. Зробити висновок.
Учні роблять висновок: отримані три кути утворюють розгорнутий кут.               Завдання 3 групі. На картках побудовані трикутники. Виміряти кути кожного трикутника за допомогою транспортира. Дані вимірювань занести в таблицю. Зробіть висновок про суму кутів трикутника.
      Після закінчення роботи кожна група представляє свої результати. За результатами доходимо висновку, що сума кутів близька до 180°, а периметр різний у всіх трикутників.

При виконанні даної роботи в учнів формується наочне представленя про суму кутів трикутника.

Фізкультхвилинка для очей

Малюємо очима трикутник,

Тепер його повертаємо вершиною вниз.

І знову очима по периметру ведемо.

Малюємо вісімку вертикально,

Тепер покладемо її на бік

А зараз нашу вісімку горизонтально поставимо

І у її центрі зупинились.

Очі примружили. А тепер – відкрили!

Фізкультхвилинка завершилась.

Учитель: Чи можемо ми стверджувати, що сума кутів будь-якого трикутника дорівнює 180˚? Або це випадковий збіг? А чи відомо вам, що в теорії Лобачевського при додаванні кутів трикутника їх сума завжди має результат менший, ніж 180º. В геометрії Рімана, сума всіх кутів трикутника більше 180º, а в працях Евкліда вона дорівнює 180˚ градусам.

Дуже часто вчені спочатку експериментальним в шляхом встановлюють важливі факти, а потім доводять їх за допомогою логічних міркувань.
Це відбувається в хімії, фізиці, біології, геометрії. Спробуємо і ми довести висновок, отриманий в результаті дослідження.
Далі йде робота в парах.

На кожній парті є листи з готовим малюнком.
Учням пропонується на цьому аркуші записати умову теореми і спробувати усно довести теорему про суму кутів трикутника.

Що стосується труднощів, можна звернутися до підказки на зворотному боці аркуша:

1.Знайти три кути, складових розгорнутого кута.

2. Деякі кути заміни рівними.

1. На рисунку назвіть пари внутрішніх різносторонніх кутів при прямих a і b і січних AB і BC.

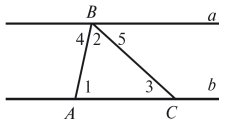
33-5 Рисунок

2. Що можна сказати про кути кожної пари (див. вище), якщо a||b?

3. Знайдіть на рисунку 3 суміжні кути з вершиною в точці B. Чому дорівнює їх сума?

4. Порівняйте суму суміжних кутів (див. вище) із сумою кутів трикутника. Зробіть висновок.

Для підготовки до сприйняття наслідку 1 можна запропонувати учням запитання:

Чи можуть бути в трикутнику:

а) два прямі кути; (ні)

б) два кути 100° і 120°; (ні)

в) два тупі кути; (ні)

г) один кут тупий, а інший — прямий? (ні)

Якщо учні дають відповіді з обґрунтуванням, то доведення наслідку 1 буде мати вигляд узагальнення проведених міркувань.

Звіримо висновок з підручником.

Як квінтесенція роботи з вивчення нового матеріалу демонструється таблиця «Сума кутів трикутника».

Сума кутів трикутника
Теорема
	A + B + C = 180° Сума кутів трикутника дорівнює 180°.
Висновки
Якщо в трикутнику ABC кут А — тупий, то він єдиний. Якщо в трикутнику ABC кут А = 90°, то він єдиний. У будь-якому трикутника ABC принаймні два кути гострі

5. Первинне усвідомлення нового матеріалу

Зміст практичного кейсу 4

І група. Задачі на безпосереднє застосування теореми.

Рівень А

Знайдіть невідомий кут трикутника, якщо два його кути дорівнюють: а) 65° і 45°; б) 120° і 18°; в) 90° і 64°.

Відповідь: а) 70˚; б) 42˚; в) 26˚.

Рівень Б

Знайдіть усі кути трикутника, якщо:

а) один із них удвічі менший за другий і на 20° більший за третій;

б) їхні градусні міри відносяться як 1 : 3 : 5.

Відповідь: а) 30˚, 50˚, 100˚; б) 20˚, 60˚, 100˚.

ІІ група. Задачі на застосування теореми про суму кутів трикутника разом із властивістю кутів рівнобедреного трикутника.

Рівень А

Знайдіть невідомі кути рівнобедреного трикутника, якщо:

а) кут при його основі дорівнює 40°;

б) кут, протилежний його основі, дорівнює 40°.

Відповідь: а) 40˚ і 100˚; б) 70˚ і 70˚

Рівень Б

Один із кутів рівнобедреного трикутника дорівнює 50°. Знайдіть решту кутів. Скільки розв’язків має задача?

Відповідь: І. 65˚ і 65˚

ІІ. 50˚ і 80˚

ІІІ група. Задачі на застосування наслідків з теореми.

Рівень А

Доведіть методом від супротивного, що кут при основі рівнобедреного трикутника не може бути тупим.

Доведення: Припустимо, що кут при основі рівнобедреного трикутника є тупим. Тоді за властивістю кутів рівнобедреного трикутника, він має два рівних тупих кута. А це не можливо, бо якщо в трикутнику є тупий кут , то він єдиний.

Рівень В

Чи може трикутник із кутом 40° дорівнювати трикутнику з кутом 140°? Відповідь обґрунтуйте.

Відповідь: Ні. Тому, що сума двох кутів уже буде дорівнювати 180˚, а ще додати третій. Це суперечить теоремі: сума кутів трикутника дорівнює 180°.

Наведені задачі рівня А можна розв’язати усно, для цього вчителю достатньо заздалегідь зробити рисунки і позначити на них відомі величини.

6. Закріплення нового матеріалу.

Яке з тверджень неправильне?

3) Якщо

4) Якщо

Відповідь: 2 і 3

33-6 Рисунок

Самостійна робота

Варіант 1

1. Знайдіть невідомий кут трикутника (рис. 1).

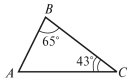
34-1 Рисунок

(рис. 1).

Відповідь:72˚

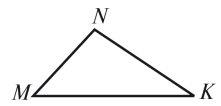
2. Знайдіть невідомі кути трикутника (рис. 2).

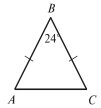
34-2 Рисунок

(рис. 2).

Відповідь: 78˚ і 78˚

3. Кут при основі рівнобедреного трикутника дорівнює 72°. Знайдіть кут при вершині.

Відповідь: 36˚

Варіант 2

1. Знайдіть невідомий кут трикутника (рис. 3).

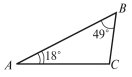
34-3 Рисунок

(рис. 3).

Відповідь: 113˚

2. Знайдіть невідомі кути трикутника (рис. 4).

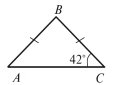
34-4 Рисунок

(рис. 4).

Відповідь: 42˚ і 86˚

3. Знайти кути рівнобедреного трикутника, якщо кут при вершині в три рази більший за кут при основі.

Відповідь: 36˚, 36˚ і 72˚

7. Підсумок уроку .

Математичний диктант:

Чи може сума кутів трикутника дорівнювати 200⁰?
Чи є правильним твердження, що в трикутнику принаймні один кут є тупим?
Чи існує трикутник з двома прямими кутами?
Чи існує трикутник з кутами 60⁰, 50⁰, 70⁰?
Сума двох кутів трикутника дорівнює 140⁰. Знайдіть третій кут.
Один кут у трикутнику прямий. Якими є два інші кути?
Знайдіть третій кут трикутника, якщо два його кути дорівнюють 40⁰ і 60⁰.

У трикутнику ABC A= 60⁰ , 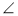B= 80⁰. Який це трикутник – гострокутний, прямокутний чи тупокутний?
Внутрішній кут при вершині С трикутника АВС дорівнює 70⁰. Чи є правильним твердження, що зовнішній кут при цій же вершині дорівнює 110⁰?
Один із зовнішніх кутів трикутника дорівнює 60⁰. Чому дорівнює сума двох внутрішніх кутів трикутника, не суміжних з ним?
У трикутнику АВС кут А прямий. Чим (катетом чи гіпотенузою) є відрізок ВС?
Один із кутів, прилеглих до катета прямокутного трикутника, дорівнює 40⁰. Чому дорівнює другий кут, прилеглий до цього ж катета?

ВЗАЄМОПЕРЕВІРКА І ОЦІНЮВАННЯ

Ні 7. 80⁰
Ні 8. Гострокутний
Ні 9. Так
Так 10. 60⁰
40⁰ 11. Гіпотенузою
Гострими 12. 90⁰

Вчитель виставляє оцінки за урок.

Прийом «Рефлексія»

- Який етап уроку був тобі самим цікавим у пізнавальному плані?

- На якому етапі ви відчули емоційний підйом?

- Який етап уроку здався тобі найбільш нудним?

- Поставте собі оцінки за урок, можна з коментарями.

- Поставте оцінку роботі всього класу за роботу на уроці, можна з коментарями.

- Що більше всього зацікавило вас на уроці і що здивувало?

- Що сподобалося більше всього?

Школярі виставляють оцінки на полях зошита. Коментуються декілька оцінок.

Учитель. Дякую всім за гарну та плідну працю!

$D:\Матеріали з ноутбука 09.2013\Математика\Відсоткові відношення\Смайлики до уроку\smiley_with_thumbs_up.gif$ $D:\Матеріали з ноутбука 09.2013\Математика\Відсоткові відношення\Смайлики до уроку\33743658-Emoticon-sveglia-con-mezzo-sorriso-Archivio-Fotografico.jpg$ $D:\Матеріали з ноутбука 09.2013\Математика\Відсоткові відношення\Смайлики до уроку\1374942091_5m6w8jswrbbftdc.jpeg$

8. Домашнє завдання.

Плиточки, що мають форму рівних рівносторонніх трикутників, викладають на площині так, що одна з вершин у них спільна, а сторони двох сусідніх збігаються. Чи можна скласти в такий спосіб “розетку” без зазорів? Якщо можна, то скільки плиточок для цього треба взяти?

Відповідь: 6

За бажанням ви можете написати казку чи, навіть, вірш про країну Чудесних Трикутників. А можете із різних видів трикутників скласти картинку. Це може бути тварина чи візерунок.

Додаток 1

Зміст інформаційного Кейсу

Трикутник
1. Означення. Елементи
	∆АВС: А, В, С — вершини; АВ, ВС, АС — сторони; A, B, C — кути
2. Периметр трикутника
Р = АВ + ВС + АС
3. Види трикутників (за кутами)
гострокутний	прямокутний		тупокутний
4. Нерівність трикутника
		\|b – c\| < a < b + c

Додаток 2

Зміст практичного кейсу 1

Група перша.

Група друга

Як провести одну лінію в довільному трикутнику, щоб розділити його на чотири фігури?

Третя група

Додаток 3

Зміст практичного кейсу 2

Група перша.

- Будуйте трикутник з двома прямими кутами.

Група друга

- Будуйте трикутник з двома тупими кутами.

Третя група

- Будуйте трикутник з тупим і прямим кутом.

Додаток 4

Зміст практичного кейсу 3

Додаток 5

1. На рисунку назвіть пари внутрішніх різносторонніх кутів при прямих a і b і січних AB і BC.

33-5 Рисунок

2. Що можна сказати про кути кожної пари (див. вище), якщо a||b?

3. Знайдіть на рисунку 3 суміжні кути з вершиною в точці B. Чому дорівнює їх сума?

4. Порівняйте суму суміжних кутів (див. вище) із сумою кутів трикутника. Зробіть висновок.

Зоротна сторона аркуша:

1.Знайти три кути, складових розгорнутого кута.

2. Деякі кути заміни рівними.

Додаток 6

Сума кутів трикутника
Теорема
	A + B + C = 180° Сума кутів трикутника дорівнює 180°.
Висновки
Якщо в трикутнику ABC кут А — тупий, то він єдиний. Якщо в трикутнику ABC кут А = 90°, то він єдиний. У будь-якому трикутника ABC принаймні два кути гострі

Додаток 7

Зміст практичного кейсу 4

І група. Задачі на безпосереднє застосування теореми.

Рівень А

Знайдіть невідомий кут трикутника, якщо два його кути дорівнюють: а) 65° і 45°; б) 120° і 18°; в) 90° і 64°.

Рівень Б

Знайдіть усі кути трикутника, якщо:

а) один із них удвічі менший за другий і на 20° більший за третій;

б) їхні градусні міри відносяться як 1 : 3 : 5.

Рівень А

Знайдіть невідомі кути рівнобедреного трикутника, якщо:

а) кут при його основі дорівнює 40°;

б) кут, протилежний його основі, дорівнює 40°.

Рівень Б

Один із кутів рівнобедреного трикутника дорівнює 50°. Знайдіть решту кутів. Скільки розв’язків має задача?

ІІІ група. Задачі на застосування наслідків з теореми.

Рівень А

Доведіть методом від супротивного, що кут при основі рівнобедреного трикутника не може бути тупим.

Рівень В

Чи може трикутник із кутом 40° дорівнювати трикутнику з кутом 140°? Відповідь обґрунтуйте.

Додаток 8

Самостійна робота

Варіант 1

1. Знайдіть невідомий кут трикутника (рис. 1).

34-1 Рисунок

(рис. 1).

2. Знайдіть невідомі кути трикутника (рис. 2).

34-2 Рисунок

(рис. 2).

3. Кут при основі рівнобедреного трикутника дорівнює 72°. Знайдіть кут при вершині.

Варіант 2

1. Знайдіть невідомий кут трикутника (рис. 3).

34-3 Рисунок

(рис. 3).

2. Знайдіть невідомі кути трикутника (рис. 4).

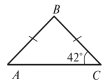
34-4 Рисунок

(рис. 4).

Література

Програма для загальноосвітніх навчальних закладів. Математика . 5-12 класи. « Перун». Київ .2005
Бабенко С. П. Геометрія. 7 клас: Розробки уроків
Нелін Є.П. Геометрія в таблицях.
Геометрія у визначеннях, формулах і таблицях: Довідковий посібник для учнів 7—11 класів. — X.: Веста: Видавництво ≪Ранок≫, 2006.
Роєва Т. Г. Геометрія в таблицях 7-9 кл. Навчальний посібник.
Роганін О.М. Тест-контроль. Алгебра + Геометрія. 7 клас: Зошит для самостійних та контрольних робіт
Погорєлов О.В., Геометрія 10-11[Текст]: підруч. для 10-11 кл. серед. шк./ О.В.Погорєлов. – К.: «Освіта», 1997. – 128 с.
Бевз Г.П., Геометрія 11[Текст]: підруч./ Г.П.Бевз, В.Г.Бевз, Н.Г.Владімірова, В.М. Владіміров. – К.: «ГЕНЕЗА», 2011. – 335 с.
Лекция 11-12 кейс-метод, кейс технология [Електронний ресурс]/НФПК – Режим доступу: http://www.openclass.ru/node/284481.

10. Вказівки до підготовки завдань за кейс-методом [Електронний ресурс]/ ПЕДКАБІНЕТ блог для викладачів СТБО – Режим доступу:

https://pedkab.wordpress.com

Доклад по математике «Применение кейс-технологий на уроках математики» [Електронний ресурс]/ VIDEOUROKI – Режим доступу: http://videouroki.net/filecom.php?fileid=98697337
Case – технологии на уроках математики [Електронний ресурс]/ Фестиваль педагогических идей «Открытый урок» – Режим доступу: http://festival.1september.ru/articles/593299/

Середня оцінка розробки

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

Загальна:

5.0

Всього відгуків: 2

Оцінки та відгуки

Могиленко Анастасія 09.05.2020 в 23:41

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0
Качанова Тетяна Василівна 13.02.2020 в 10:10

Гарний урок. Дякую. Буду викорстовувати у своїй роботі.

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0