Урок "Теорема Піфагора"

Урок  геометрії.  8 клас 

Л. Т. Фисина, с. Олександрівка, Снігурівський р-н, Миколаївська обл.

Тема. Теорема Піфагора

Мета. Ознайомити учнів з теоремою Піфагора; довести теорему Піфагора та сформулювати наслідки з неї; формувати вміння відтворювати зміст вивчених тверджень та використовувати їх під час розв’язування задач; удосконалювати навички самостійної діяльності учнів, роботи в малих групах; поглибити знання учнів з історії математики; розвивати логічне мислення, увагу, спостережливість, застосування знань у реальних життєвих ситуаціях. 

Тип уроку. Засвоєння нових знань.

Обладнання та наочність.  Презентація «Піфагор», аркуші із завданнями (для кожного учня). Вислів індійського математика Бхаскари «Я глибоко шаную математику, бо обізнані з нею мають у ній засіб до розуміння всього існуючого; вона – основа всього видимого ». Картки оцінювання. 

Підручник. Геометрія: підручник для 8 класу загальноосвітніх навчальних закладів/А. Г. Мерзляк, В. Б. Полонський, М. С. Якір  - Харків «Гімназія», 2016/.

ХІД УРОКУ

І. Організаційний момент

Налаштування учнів на роботу. Працюємо так, щоб в кінці уроку ви змогли підсумувати кількість набраних балів у картці оцінювання. 

Хочу зачитати слова індійського математика ХІІ ст. Бхаскари «Я глибоко шаную математику, бо обізнані з нею мають у ній засіб до розуміння всього існуючого; вона – основа всього видимого ».  Вона допоможе при вивченні інших наук тому, що розвиває логічне та критичне мислення, уміння узагальнювати, аналізувати, порівнювати та робити висновки.

ІІ. Перевірка домашнього завдання

1). Доповідають консультанти про наявність домашнього завдання.

2). Учні обмінюються зошитами із сусідом по парті та перевіряють правильність виконання домашнього завдання за зразком на дошці.

3). Гра «Хрестики - нулики». Клас ділиться на дві команди: «Хрестики» та «Нулики».

Згадайте.

1. Який трикутник називають прямокутним?

2. Які назви мають сторони прямокутного трикутника?

3. Чому дорівнює сума гострих кутів прямокутного трикутника?

4. Що більше: гіпотенуза чи катет прямокутного трикутника?

5. Чому дорівнює катет прямокутного трикутника, що лежить проти кута 30°?

6. Чому дорівнює медіана прямокутного трикутника, проведена до гіпотенузи?

7. Знайдіть висоту прямокутного трикутника, якщо вона проведена до гіпотенузи і ділить її на відрізки, що дорівнюють 3 см і 12 см.

8. Знайдіть висоту прямокутного трикутника, якщо вона проведена до гіпотенузи і ділить її на відрізки, що дорівнюють 9 см і 4 см.

9. Висота прямокутного трикутника, що проведена до гіпотенузи  ділить її на відрізки завдовжки 9 см і 16 см. Знайдіть більший катет. (20 см)

4). Гра «Математичне лото». На столі вчителя лежать картки з відповідями до завдань, на зворотній стороні яких написані літери «П», «І», «Ф», «А», «Г», «О», «Р», «Е». Літери магнітами кріпляться на металеву дошку. Отримуємо слово «ПІФАГОР». 

Завдання 1.

Трикутник АВС – прямокутний. Назвіть проекції катетів на гіпотенузу. (ВD і AD – П)        

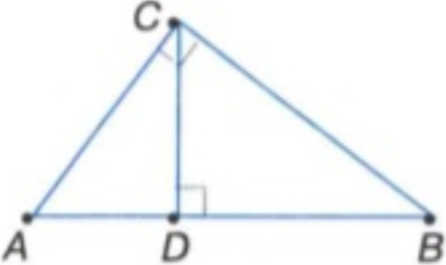
Завдання 2. Трикутник АВС – прямокутний.  Знайдіть гіпотенузу.  (25 – І )                                                 

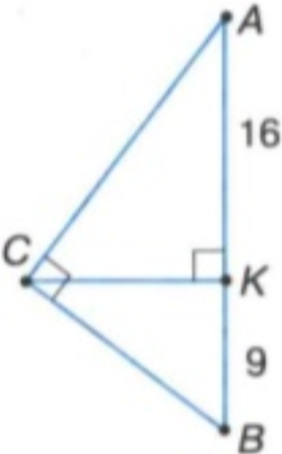
Завдання 3. Трикутник АВС – прямокутний. Знайдіть більший катет. (20 – Ф)                                                           

Завдання 4. Трикутник АВС – прямокутний. Знайдіть менший катет. (15 – А)

Завдання 5. Трикутник АВС – прямокутний. Знайдіть висоту, проведену на гіпотенузу. (12 –Г)

Завдання 6. Чи може відношення катета до гіпотенузи прямокутного трикутника бути меншим від одиниці? ( Так – О, Ні – Е)

Завдання 7.За рисунком визначте довжину відрізка х. (2 –Р) 

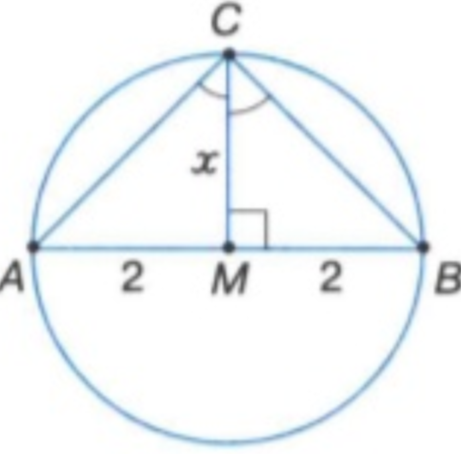
ІІІ. Формулювання теми та мети уроку

1). Презентація «Піфагор».

2). Доведення теореми Піфагора.

3). Наслідки. с = ; a = ; b = .

ІV. Застосування знань, закріплення вмінь та навичок

1). Вправа «Знайти зашифроване слово» (УСПІХ)

1. Використайте теорему Піфагора для трикутника KЕM, у якого = 90°. 

А) ЕМ² = ЕК² + КМ²;   О) ЕК² = ЕМ² + КМ²;  Ж) КМ² = ЕМ² + КЕ².

1. Використайте теорему Піфагора для трикутника KLM, у якого = 90°.

А) КМ² = КL² + МL²;  У) КL² = КМ² + МL²;  В) МL² =КL² + КМ².

2.  Використайте наслідок з теореми Піфагора для трикутника АВС, у якого = 90°. 

О) АВ = ;   К) ВС = ;  С) АВ =

3. Якщо в трикутнику PRS виконується рівність PS² = PR² + RS², то прямим кутом є:

А) П) ;  Л)

 4. Знайдіть гіпотенузу прямокутного трикутника, якщо катети дорівнюють см і 1 см.

Б) 3;  В) 1;  І) 2.

5. Знайдіть катет прямокутного трикутника, якщо гіпотенуза і другий катет відповідно дорівнюють см і 1 см.

Л) 1;  Х) 2;  М) 3. 

6. Визначте, який із кутів трикутника АВС прямий, якщо АВ = 3 см, ВС = 4 см, АС = 5 см.

К)      Р)

2). Графічний диктант (так  - ^     , ні - _ )

1. Якщо в трикутнику АВС °, то АВ² = АС² + ВС².

2. Якщо в трикутнику MNP P = 90°, то MN² = MP² + PN².

3. Якщо в трикутнику XYZ виконується рівність  XY² = XZ² + YZ², то прямим є кут Х.

4. Якщо в трикутнику MКP К = 90°, то MК² = MР² - PК².

( Відповідь ^^-^)

V. Узагальнення знань учнів

Самостійна робота

№ 529 (по варіантах: 1в. - 1. 5 см, 2 в. - см)  

№ 530 (по варіантах: 1 в. – 9 см, 2 в. – 6 см)

№532.

Робота в групах

1 група

№ 539 (21 + 35 + 28 = 84(см))

2 група

№ 540 (10 см, 24 см)

3 група

Один з катетів прямокутного трикутника 5 см. А другий – менший від гіпотенузи на 1 см. Знайдіть сторони трикутника. (12 см, 13 см)

4 група

Катети прямокутного трикутника відносяться, як 3:4, а гіпотенуза дорівнює 25 см. Знайдіть катети трикутника. (15 см, 20 см)

VІ. Домашнє завдання. Підведення підсумків

1). Опрацювати П.16, вивчити теорему та наслідки.

№ 531 (1 в. – 1 та 2 випадки, 2 в. – 1 та 3 випадки),

№ 533, № 535.

2). Оформлення карток оцінювання