Урок "Теорема Піфагора"

Тема. Теорема Піфагора

Мета:

навчальна: сформувати в учнів розуміння змісту теореми Піфагора та її доведення; формувати вміння відтворювати зміст теореми Піфагора; застосовувати її формулювання для розв'язування задач на знаходження невідомих сторін прямокутних трикутників; довести теорему різними способами;

розвивальна: розвивати логічне, критичне мислення учнів, стимулювати їх пізнавальну діяльність; розвивати вміння учнів аналізувати,  зіставаляти, робити висновки;

виховна: виховувати  прагнення до самовдосконалення; охайність побудови малюнків та культуру записів на дошці і в зошиті; прививати в учнів любов до геометрії.

Типу уроку: засвоєння нових знань.

Хід уроку

1. Організаційний етап

Учитель. Доброго ранку, діти! З яким настоєм ви прийшли на сьогоднішній урок?

З’ясування емоційної готовності учнів до уроку (вправа «Світлофор»). Учні піднімають картки:

- готовий до уроку (зелений колір);

- готовий частково (оранжевий колір);

- не готовий зовсім (червоний колір).

Учитель. Я радий, що сьогодні переважає зелений, а це означає, що ви готові до праці. Сподіваюся, що на уроці, нас чекає успіх, якщо ми працюватимемо організовано і будемо компетентними в запропонованих задачах.

Світ, що нас оточує, - це світ геометрії. Тому запрошую вас до його пізнання. І нехай сьогоднішній урок стане ще одним віконцем у дивовижний і цікавий математичний простір.

Я надіюсь на нашу співпрацю, свідоме засвоєння матеріалу уроку.

ІІ. Формулювання теми і мети уроку; мотивація навчальної діяльності:

Сьогодні на уроці я пропоную вивчити: теорему нареченої, теорему німфи, теорему метелика, теорему 100 биків, розглянути «втечу убогих» і «міст ослів».

У вас може виникнути запитання: чому так багато теорем на один урок? Цілком вірно: ці назви стосуються всього однієї теореми і має вона назву «Теорема Піфагора». Саме так і буде звучати сьогоднішня наша тема, тому відкрийте будь ласка ваші зошити і запишіть 3 березня, класна робота, Тема Теорема Піфагора.

Отже, ми сьогодні вивчимо теорему Піфагора.

Теорема Піфагора – одна з основних у геометрії. Завдяки їй можна довести та розв’язати не одну задачу. Тому її потрібно добре засвоїти.

Сьогодні у нас урок однієї теореми, на якому ми познайомимося з декількома способами її доведення (а відомо понад 300 різних доведень, а звучить ця теорема так : Квадрат гіпотенузи дорівнює сумі квадратів катетів.

Що ж давайте спробуємо це довести.

ІІІ. Доведення теореми Піфагора.

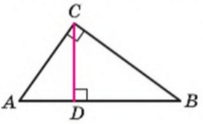Дано: ∆АВС, С=90º.

Довести: AB²=АС² + BC²

Доведення

Розглянемо АСВ. Що ви можете про нього сказати? Проведемо висоту CD. Застосувавши теорему про метричні співвідношення для катетів АС і ВС, отримаємо:

АС² = AB  АD

BC²= AB  DВ

 АС² + BC² = AB  АD + AB  DВ= AB (АD + DВ) = AB  AB = AB²

Якщо в прямокутному трикутнику довжини катетів дорівнюють a і b, а довжина гіпотенузи с, то т.Піфагора можна виразити такою рівністю

Доведення 2: за допомогою розробки.

ІV. Первинне закріплення матеріалу.

Оскільки на уроці розпочинається робота із формування вмінь застосовувати теорему Піфагора, то слід одразу виробляти в учнів навички математичної культури, тобто застосуванню теореми Піфагора для деякого прямокутного трикутника мають передувати такі міркування:

А зараз пропоную вам провести експеримент – ви отримуєте мотузку із 12 вузлами. Вам необхідно буде утворити трикутники із сторонами 3,4 і 5 рівних відрізків та визначити вид даних трикутників.

Ще  в  Давньому  Єгипті  була відома  теорема, яка потім дістала  назву  „ТЕОРЕМА  ПІФАГОРА”.

Вона застосовувалась тоді для побудови  прямих   кутів  на місцевості за допомогою мотузки з вузликами, яку натягували у вигляді трикутника зі сторонами 3,4 і 5 вузлів.

Та заслуга Піфагора в тому, що він першим її довів.

Теорема Піфагора - одна із найголовніших теорем геометрії.

Але, крім того, теорема Піфагора має велике практичне значення: вона застосовується в геометрії  і в житті буквально на кожному кроці.

Жарт:

Один професор скористався теоремою Піфагора на практиці. Йому запропонували ліжко, що виявилось коротким для нього. Не розгубившись той, виміряв довжину і ширину ліжка – a і b, і побачив, що його власний зріст менший від . Тоді математик зручно вмостився на ліжку по діагоналі, остаточно впевнившись у великій практичній користі теореми Піфагора.

V. Розв’язування задач на застосування теореми Піфагора.

Діагональ прямокутника дорівнює 10см, а одна з його сторін 8см. Знайдіть периметр прямокутника.

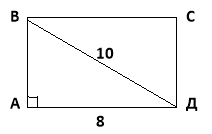                                                    Дано: АВСД – прямокутник,

ВД – діагональ,             

                                                    ВД = 10см,  АД = 8 см.

Знайти: Р.

І так, яку ж теорему ми сьогодні вивчили? Щоб дати відповідь на ц запитання пропоную вам розгадати кросворд, у виділеній частині якого ми і дізнаємося її назву.

Кросворд

1.Чотирикутник, у якого дві сторони паралельні, а дві інші – не паралельні.

           (Трапеція)

2.Найбільша із сторін прямокутного трикутника.   (Гіпотенуза)

3.Трикутник – це ..., яка складається із трьох точок, що не належать одній прямій, і трьох відрізків, попарно з’єднуючих ці точки.                                               (Фігура)

4.Одна із сторін трикутника, що утворюють прямий кут.  (Катет)

5.Наука, яка вивчає властивості геометричних фігур.   (Геометрія)

6.Перпендикуляр, проведений із вершини трикутника на протилежну сторону.                                                                                                                                             (Висота)

7.Прямокутник, у якого всі сторони рівні.                              (Квадрат)

VІ. Підсумок уроку. Рефлексія

Сьогодні на уроці ми вивчили теорему Піфагора, навчились використовувати її при розв'язанні задач. Давайте ще раз сформулюємо теорему Піфагора.

Інтерактивна вправа “Незакінчені речення”.

1.               Сьогодні на уроці ми дізналися…
2.               На сьогоднішньому уроці найважливішим відкриттям для мене було…

 «Оберіть колір вашого настрою» учні визначають свій настрій, З’ясування емоційної готовності учнів до уроку (вправа «Світлофор»). Учні піднімають картки:

- готовий до уроку (зелений колір);

- готовий частково (оранжевий колір);

- не готовий зовсім (червоний колір).

Урок має свої часові межі, але бажання пізнати більше має бути безмежним. Ми дізналися лише дещицю того, що можна знайти цікавого про терему Піфагора.

Працюйте, шукайте, поглиблюйте свої знання.

VІІ. Домашнє завдання