Урок Теорема Піфагора

Про матеріал

Конспект уроку містить матеріали, необхідні для узагальнення теми "Теорема Піфагора".

Перегляд файлу

Тема. Розв'язування прикладних задач на застосування теореми Піфагора

Мета:

формування математичної компетентності (формування поняття про теорему Піфагора та вироблення вмінь і навичок застосовувати набуті знання під час розв'язування пракфтичних задач);
перевірити знання учнів з теми «Метричні співвідношення у прямокутному трикутнику. Теорема Піфагора» з метою подальшої корекції;
використання математичних методів у життєвих ситуаціях;
формування культури усних та письмових обчислень;
розширити знання учнів про особистості видатних математиків;

формування компетентності вміння вчитися впродовж життя (формування уміння визначати мету навчальної діяльності, відбирати й застосовувати потрібні знання та способи діяльності для досягнення цієї мети;
знаходити зв'язок з раніше вивченим: переносити набуті знання в нові ситуації);
стимулювання учнів до висловлювань без побоювань помилитися; формування компетентності спілкування державною мовою (формування умінь ставити запитання і розпізнавати проблему;
міркувати, робити висновки;
розуміти, пояснювати і перетворювати тексти математичних задач (усно і письмово), грамотно висловлюватися рідною мовою);

формування соціальної і громадянської компетентності (уміння висловлювати власну думку, слухати і чути інших, оцінювати аргументи та змінювати думку на основі доказів);
формування компетентності ініціативності та підприємливості (формувати уміння вирішувати життєві проблеми, аналізувати, прогнозувати).

ключові компетентності:

спілкування державною мовою – розуміти, пояснювати і переказувати тексти математичних задач; доречно та коректно вживати в мовленні математичну термінологію;
математична компетентність – оперувати числовою інформацією;
навчально-пізнавальна – застосовувати різні методи пізнання, володіння вимірювальними навичками;
комунікативна – уміння взаємодіяти з однолітками, навички роботи в групі, навички володіння різними соціальними ролями;
загальнокультурні – уміння до взаємоповаги, до здорового суперництва, охайності в записах, працьовитості, уміння вислухати інших, уміння бути активним, дисциплінованим, самокритичним, самостійним (самостійно працювати з дидактичними завданнями), уміння самоконтролю.

Тип уроку: удосконалення знань і вмінь

Обладнання: демонстраційно-креслярське приладдя, ілюстрації до задач

Хід уроку

I. Організаційний момент

За календарем скоро весна. Пора пробудження, натхнення, кохання. Але в повітрі ще відчувається прохолода, яка віддзеркалює сум у наших душах. Але я раджу вам запозичити досвід Олександра Дюма, який, коли чекав гостей на звану вечірку, у гардеробі вішав табличку з написом: «Отут, за дверима, разом із одягом, залишайте свій поганий настрій».

Отож, шановні, я впевнена, що ви теж залишили свій негатив, коли такий був, за дверима класу і налаштувалися на роботу.

«Геометрія володіє трьома скарбами

Одне з них - теорема Піфагора»

Сьогодні ми маємо можливість знову доторкнутися до тієї міри золота, якою Йоганн Кеплер назвав…(теорему Піфагора). Теорема Піфагора є тим золотим ключиком, який дозволяє відкрити двері до багатьох загадок і задач, дає можливість виконувати наукові розрахунки траєкторій польоту літаків і ракет, руху небесних тіл, визначати відстані до доступних і недоступних точок, висоту будівель, знаходити площі фігур. Без теореми Піфагора геометрію уявити собі дуже важко

Ми перевіримо, наскільки добре вивчили та зрозуміли цю визначну теорему, а також закріпимо навички використання цієї теореми для розв’язування задач, в тому числі і прикладних.

А гаслом цього уроку я обрала слова чоловіка, якого довгий час не допускали до участі до змагань з боротьби через його малу масу, та який завдяки своїй наполегливості зумів стати врешті-решт стати олімпійським чемпіоном:

Тимчасова невдача краще, ніж тимчасова удача.

Піфагор

Отож, удачі нам усім, і хай вона буде не тимчасовою!

ІІ Оголошення теми, мети уроку

(Дванадцяте лютого Класна робота Розв’язування задач)

ІІІ. Мотивація навчальної діяльності учнів

Діти понад усе люблять секрети. І ви, я думаю, також. У вас на партах є секретні листівки. Напишіть у них, чого ж ви очікуєте від сьогоднішнього уроку, виходячи з теми. Обміняйтесь із сусідом по парті. Але не озвучуйте.

В кінці уроку побачимо, чи збудеться задумане вами. І наші гості теж поділяться між собою своїми сподіваннями.

ІV. Актуалізація опорних знань

Усне опитування

-для яких геометричних фігур можна застосувати теорему Піфагора?

- який трикутник називається прямокутним?

- як називаються сторони прямокутного трикутника?

- яка сторона трикутника називається гіпотенузою? Катетами?

-сформулювати теорему Піфагора

- сформулювати теорему, обернену до теореми Піфагора

2. Для закріплення теорії напишемо графічний диктант:

Трикутник з кутом 90 ̊ називається прямокутним
Єгипетським називають прямокутний трикутник із катетами 3 і 4 та гіпотенузою 5?
Щоб знайти квадрат гіпотенузи, треба додати квадрати катетів? (+)
Сторона, що лежить навпроти прямого кута – катет
Якщо трикутник прямокутний та рівнобедрений, то його гострі кути по 60̊
Сума гострих кутів прямокутного трикутника дорівнює 90 ̊
В прямокутному трикутнику навпроти кута в 30 ̊ лежить катет, що дорівнює половині гіпотенузи
Сторони, що утворюють прямий кут називають катетами

+++--+++

Повторення формул .

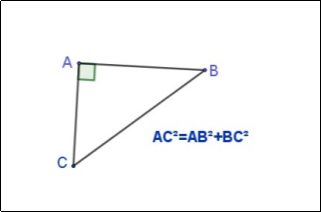
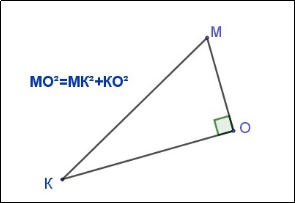
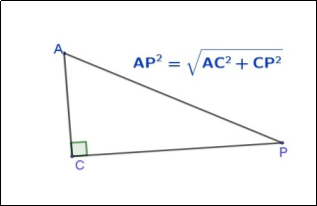
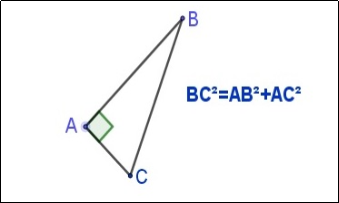
Гра «Вірно-невірно». Дано 10 рисунків та формули для обчислення певних елементів трикутника. Розподілити на 2 групи : правильні чи неправильні вказані формули

ПЕРЕВІРКА: вірно:5,6,7,8,10

невірно:1,2,3,4,9

Усне розв’язування задач

Гра «Знайди пару»

ІІІ. Систематизація та узагальнення знань

Ми повторили вивчений матеріал і будемо застосовувати його до задач. Чи замислювався хтось з вас, що дорога до школи – це прямокутні трикутники? Ось ми і розглянемо наш маршрутний лист «Школа-дім»

Наше село- це 4 паралельні вулички, а провулки поділяють його на прямокутники. Ми розглянемо окремі частини вашого шляху та подумаємо: а чи змогли б ви визначити переміщення, яке ви при цьому здійснюєте. Звичайно, бо в нас утворюються прямокутні трикутники, для яких можна застосувати теорему Піфагора.

Отож, наш маршрутний лист:

Саша до вул. Центральної: 4096+5041=9137 (96м)

Ліза до вул. Центральної до зустрічі з Сашою: 15129+4096=19225 (139м)

Ліза до вул. Центральної до зустрічі з Богданом: 8836+4096=12932 (114м)

Даша до вул. Центральної: 13689+252004=265693 (515м)

Богдан до зустрічі з Лізою, якщо відомо, що від Даші до нього 207 м

42489-13689=29160 (171м)

До Юлі від провулка, якщо відомо, що від неї до Саші 216 м.

46656-4096=42560 (206м) 206-71=135м

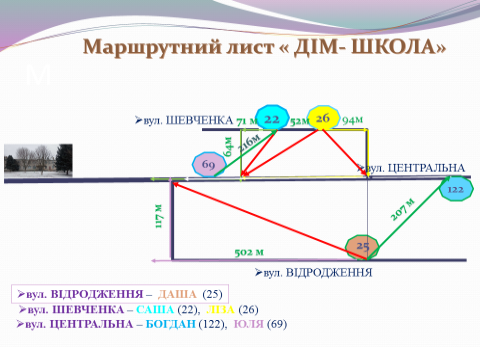
При цьому я нагадую, що ви йдете до школи притиснувши ліву ручку до узбіччя, тобто назустріч транспорту

ІV. Хвилина здоров’я .

«Вправа «Ходіння по калюжах»

Вправа виконується сидячи або стоячи.

Уявіть собі, що ви йдете по калюжах, намагаючись не промочити ніг. Ви взуті в кросівки; на високих підборах; у вас зламався каблук; в замшевих чоботах; в ризових чоботах.

Вправи для зняття втоми очей.

Швидко кліпати очима протягом 15 с.
Заплющити очі. Не відкриваючи очей, начебто подивитися ліворуч на рахунок „раз-чотири”, повернутися у вихідне положення. Так само подивитися праворуч на рахунок „п’ять-вісім” і повернутися у вихідне положення. Повторити 5 разів.
Спокійно посидіти із закритими очима, розслабившись протягом 5 с.

ІV. Удосконалення знань і вмінь

Техніка «Сигнали рукою». Учитель зупиняє пояснення і просить учнів показувати йому сигнали рукою, які свідчать про розуміння або нерозуміння матеріалу. Для цього вчитель заздалегідь домовляється з учнями про ці сигнали:

Я розумію __________ і можу пояснити (великий палець руки спрямований вгору).
Я все ще не розумію _________ (великий палець руки спрямований в бік).
Я не зовсім впевнений в _______________ (помахати рукою).

Подивившись на сигнали, учитель пропонує деяким учням висловитися:

тим, хто не зрозумів, задає питання: «Що саме вам незрозуміло?»;
слово надається тим, хто не дуже впевнений у правильності відповіді;
слово надається тим, хто все зрозумів.

Колективне розв’язування задач

Задача 1. ( для пожежників) Якої довжини має бути драбина, щоб її можна було б приставити до вікна, що знаходиться на висоті 6 м від землі, коли відстань від нижнього кінця драбини до будинку повинна дорівнювати 2,5 см?

Розв’язання.
Так як стіна перпендикулярна до землі драбина і стіна утворять прямокутний ∆АВС ( <С= 90°)
За теоремою Піфагора
АВ = АС² + СВ² =
С В² = 35 + 6,25 = 42,25

СВ = 6,5 ( м)
Відповідь: 6,5 м.

Задача 2. Телевізійна вишка підтримується чотирма канатами, прикріпленими до неї на відстані 12 м від землі і на відстані 5 м від основи вишки. Скільки метрів мотузки потрібно, якщо на вузли витратили 10 м (рис. 2)?

Розв’язання:

За теоремою Піфагора

(м) – довжина однієї мотузки

13 · 4 + 10 = 62 (м)

Відповідь. 62 м.

Задача 3. Ескалатор метрополітену має 160 сходинок від підлоги наземного вестибюлю до підлоги підземної станції. Ширина сходинки 20см, висота – 15см. Знайдіть довжину ескалатора АК. ( один учень розв’язує коло дошки задачу з поясненням, а інші за ним записують в зошити )

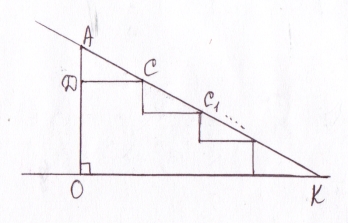мал 7 3 Розв’язання:

За теоремою Піфагора

(см) – довжина ескалатора над однією сходинкою

25∙160 = 400 (см)= 40(м)

Відповідь. 40 м.

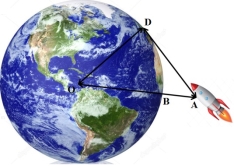
Задача 4 Космонавт під час польоту знаходиться на відстані 327 км над землею. На якій відстані від корабля знаходились у цей час найбільш віддалені від нього видимі ділянки поверхні Землі? (Радіус Землі ≈ 6400 км.)

Розв’язання

АО=АВ+ВО=327+6400=6727 (км).

(км).

Відповідь. 2071,84 км

Гра «Вірю – не вірю»

1.У Франції та Німеччині в епоху середньовіччя теорему Піфагора називали «ослячим мостом».

Відповідь: У Франції і деяких областях Німеччини в Середні віки теорему Піфагора називали «містком віслюка». Це тому, що учнів, які завчили теорему напам’ять, але не розуміли її, називали віслюками, для яких вона була ніби непрохідним мостом.

2. Чи вірите ви , що Теорема Піфагора має 999 доведень?

Відповідь: Теорема Піфагора - одна з найбільш відомих і старих теорем, має щонайменше 367 доведень.

3. У математиків арабського Сходу ця теорема отримала назву «теореми нареченої». Чому?

Відповідь: У математиків арабського сходу «теорема нареченої» (Евклід називав «теорема німфи» через подібність рисунка з метеликом. Але цим словом греки називали деяких богинь. а також наречених. Перекладаючи, араби не звернули увагу на креслення і переклали слово «німфа» як «наречена», а не як «метелик»).

4. Чи правда, що довівши свою знамениту теорему, Піфагор віддячив богам, принісши їм у жертву 100 биків?

Відповідь: Легенда говорить, що коли Піфагор сформулював І довів теорему, то приніс у жертву богам 100 биків, звідси й пішла друга назва теореми - «гекатомба» (сто биків). Але ця легенда, швидше за все, вигадана, адже він був вегетаріанцем і непримеренним супротивником пролиття крові тварин.

5. Чи вірите ви , що в 1995 року в Єгипті було випущено поштову марку, що ілюструє теорему Піфагора

Відповідь: ні. 1995 року в Греції було випущено поштову марку, що ілюструє теорему Піфагора. Дивлячись на неї, можна наочно пересвідчитись в тому, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.

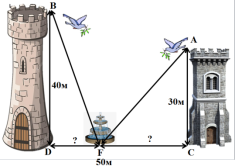Задача 5. «Дві вежі» (задача Фібоначчі- італійський математик ХІІІ ст.)

Дві вежі висотою 30 і 40 футів, розміщено одна від одної на відстані 50 фунтів. Між ними знаходиться фонтан, до якого одночасно з маківок веж з однаковою швидкістю вилетіли два голуби. Яка відстань від

фонтана до кожної з двох веж, якщо голуби долетіли до фонтана одночасно.

Дано: АС=30 (фут) ВD=40(фут) CD=50(фут) Знайти: СF; FD

Розв’язування:

AF=BF;

Нехай CF=x, FD=50-x.

Фут - довжина ступні людини.

AC 2 + CF 2 = FD2 + BD2

302 + x 2 = (50 - x)2 + 402

302 + x 2 = 502 -100x + x 2 + 402

100x = 502 - 302 + 402

100x = 20 ´ 80 + 402

100x = 1600 + 1600

x = 16 + 16

x = 32

CF = 32(фут)

FD = 50 - 32 = 18(фут)

Відповідь: CF=32, FD=18.

Задача Бхаскари (індійський математик ХІІ ст.)

Над озером тихим, з

півфута заввишки

виситься лотоса квітка.

І вітер поривчастий

відніс її вбік. Нема

більше квітки над водою.

Знайшов рибалка її

у двох футах від місця, де росла.

Отже, пропоную питання:

як озера вода тут глибока?

V. Підсумок уроку

1. Підведемо підсумок , відповівши на чотири «що?»

Що найбільше запам’яталося на уроці?
Що не сподобалося?
Про що хотілося б дізнатись більше ?
Що дізнався нового?

Рефлексія

Які риси характеру допомагали вам досягти успіху на уроці?
Які заважали?

активність пасивність упертість

дисциплінованість лінь ввічливість

неуважність допитливість недбалість

організованість незібраність уважність

ініціативність наполегливість недбалість

відповідальність працелюбство

Ось і наближається дзвінок. Дякую вам за гарну роботу. А за неї годиться й гарна винагорода – високі бали.

САМООЦІНЮВАННЯ РЕЗУЛЬТАТІВ УРОКУ

я уважно слухав (ла) пояснення учителя _________ балів
я активно працював (ла) на уроці ____ балів
я приймав (ла) участь в аналізі задач,

та мої пропозиції були враховані при розв’язуванні задач____балів

я допомагав (ла) своїм однокласникам, заохочуючи їх до роботи

у класі_____________________ балів

Підбиття підсумків ___________ балів

А я вам хочу побажати: Нехай ваші

Праця

Ідеї

Фантазія

Активність

Гумор

Оптимізм

Розум

допоможуть вам весь рік працювати так дружно і завзято, як сьогодні на уроці, а теорема Піфагора нехай буде не ослячим, а веселковим місточком до нових знань та здобутків!

І наостанок:

Життя – театр, а всі ми в нім актори,
Ми знаємо багато різних див,
Та пам’ятати будем Піфагора,
Що теорему «золоту» створив.