Урок з геометрії у 8 класі на тему "Теорема Піфагора. Розв'язування задач"

Урок з геометрії у 8 класі

Тема уроку: розв’язування прямокутних трикутників

Мета уроку: 1)повторити теорему Піфагора, перевірити як учні її розуміють; 

                        розглянути наслідки, що випливають з теореми Піфагора,

                        єгипецький трикутник; формувати вміння застосовувати

                        теорему Піфагора для знаходження невідомих сторін

                        прямокутного  трикутника;

                     2) формувати уміння чітко, зрозуміло, лаконічно виражати свою

                         думку державною мовою, аргументовано доводити  правиль-

                         ність своїх дій; вчити підбирати потрібні знання, щоб  застосу- 

                         вати їх в житті

Тип уроку: застосування знань і вмінь.

Обладнання та наочність: підручник, креслярські прилади, заготовлені малюнки, заготовлені задачі, комп’ютер з інтернетом.

Хід уроку

І. Організаційний момент

 

ІІ. Перевірка домашніх завдань

1. Які бувають трикутники в залежності від сторін (означити, три учнгі будують на дошці трикутники: рівносторонній, рівнобедрений, різно-сторонній)
2. Назвати елементи трикутника
3. Які бувають трикутники в залежності від кутів ( побудувати три-кутники: гострокутній, прямокутній, тупокутній). Дати озачення.
4. Чи може бути у трикутнику два( три) прямі кути?
5. Чи може бути у трикутнику два( три) тупі кути?
6. Поясни, доведи чому.
7. Як називаються сторони прямокутного трикутника?
8. Сформулювати теорему Піфагора
9. Як  знайти невідомий катет прямокутного трикутника?
10.  Як  знайти гіпотенузу прямокутного трикутника?

Задачі за готовим малюнком

 

 

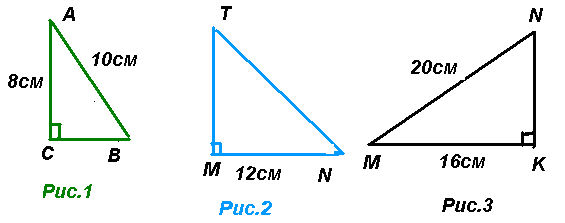
ІІІ. Удосконалення знань і вмінь.

        Попрацюємо з інтернетом. Знайдімо інформацію про єгипецький трикутник та ознайомимось цією інформацією.

 То що це за такий трикутник?

Чому називається єгипецьким?

 

 

Робота з підручником

Розв’язування задач.

1. Задача № 16  [ 2, cт.107]

     Між двома фабричними будівлями побудовано похилий жолоб для транс-портування матеріалів.Відстань між будівлями дорівнює 10 м, а кінці жолоба розташовані на висоті 8 м і 4 м над землею.Знайти довжину жолоба.

Задача № 2. Із підручника “Математика” Л.П. Магницького. Сталося якомусь чоловіку до стіни драбину поставити, стінки ж тої висота є 117 стоп.  І відати хоче він, на скільки стоп драбини нижній кінець від стіни отстояти має, якщо драбини довжина 125 стоп.

       Розв’язання: з Δ BCА – прямокутний трикутник : АС²=   АВ² – ВС²,

АС² = 125 -117 =15625 – 13689 = 1936 ;  АС =  44 ( стоп ).Відповідь:  44 стоп

Задача 3. Менша основа прямокутної трапеції дорівнює 9 см, більша її діагональ – 17см, а висота – 8 см. Знайти периметр трапеції.

Розв’язання: АВСН – прямокутник, ВС = АН = 9 см,  АВ = СН = 8 см,

ВD = 17 cм.

З  ΔВАD, кут А – прямий,   АD² = BD² + AB²;   АD² = 289 – 64 = 225 ,

AD = 15 cм,   HD = AD – AH = 15 cм - 9 см = 6 см.

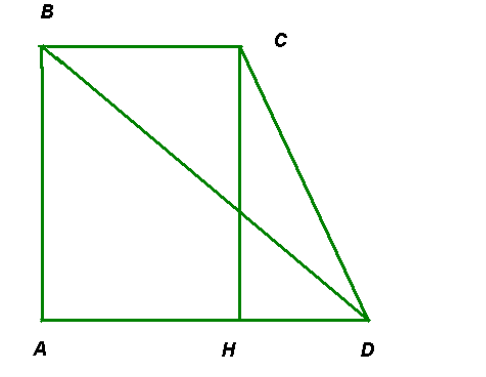
З  ΔСНD, кут Н– прямий,   СD² = НD² + СН²;  СD² = 64 + 36 = 100,

CD = 10 cм.  Р_ABCD = AB +BC + CD + AD  = 8 см + 9 см + 10 см + 15 см  =

= 42 см .     Відповідь:  42 см

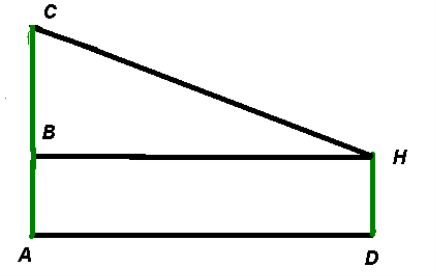
    Задача 4. За  40 м одна від одної ростуть дві ялинки. Чи можна обчислити відстань між верхівками ялинок, якщо висота однієї 31 м, а висота другої –

 6 м ?

Розв’язання: АС = 31 м, DH = 4 м, АD = BH = 40 м,  СВ = АС – АВ = 27 м,

ABHD – прямокутник.     З  ΔBHC,  СВН = 90⁰ ,       СН² = ВС² +  ВН² ,    СН² = 1600 + 729 = 2329 (м² ), СН =   48,3 м.   Відповідь.  48,3 м.  

                   

ІУ. Підбиття підсумків уроку. Рефлексія

 

У. Домашнє завдання :

1. Завдання за підручником: вчити п. 16   , виконати № 535, 538 [ 1, ст.117 ]

 

 

 

 

                          Список використаних джерел:

1. Геометрія : підрруч. для 8 кл. загальноосвіт. навч. закладів /А.Г.Мерзляк,

    В.Б. Полонський, М.С. Якір. – Х.: Гімназія, 2016. – 208 с.

2. Погорєлов О.В. Геометрія: Планіметрія: підрруч. для 7-9 кл. загальноосвіт.

    навч. закл.-   6-те вид.- К.: Школяр, 2004.- 240 с. 

 

 

 

                                 Інтерне ресурси 

Піфагор. Єгипетський трикутник. [ Електронний ресурс ]- Режим доступу:

           Вікіпедія