Урок на тему "Ділення з остачею. Конгруенції та їх властивості"

Цикл уроків з алгебри на тему «Основи теорії подільності»

для 8 класів з поглибленим вивченням математики 

                підготувала вчитель математики

 НВК: Гайсинська СЗШ-інтернат І-ІІІ ступенів  - гімназія

 Дем´янюк Ганна Володимирівна

Урок №3

Тема: Ділення з остачею. Конгруенції та їх властивості

Мета: Вдосконалити вміння учнів знаходити неповну частку та остачу, оперувати з конгруенціями; розвивати розумові операції, вміння аналізувати, порівнювати, узагальнювати, класифікувати, розмірковувати за аналогією; виховувати самостійність, організованість і мотиви діяльності.

Тип уроку: комбінований урок

Обладнання: підручник, презентація

Хід уроку:

1. Актуалізація знань

  - у формі роботи в парах (взаємоперевірка)

1. Вiдомо, що a кратне 3, b кратне 8. Доведiть, що ab кратне 24.

2. Число a кратне 6. Доведiть, що a² -12a кратне 36.

3. Доведiть, що n ²+3n дiлиться на 2 при будь-якому натуральному n.

4. Доведiть, що n³+ 5n дiлиться на 3 при будь-якому натуральному n.

5. Доведiть, що сума кубiв трьох послiдовних натуральних чисел дiлиться на 9.

6. Доведiть, що 2008⁴- 42⁴ дiлиться на 2050.

2. Пояснення нової теми  (презентація)

Якщо натуральне число а не ділиться націло на натуральне число , то можна виконати ділення з остачею. Розширимо поняття «ділення з остачею» на випадок, коли ділене є цілим числом.

Теорема:    Для будь-якого цілого числа а і натурального числа b існує єдина пара цілих чисел q і r таких, що а = bq+ r, де 0 r < b.

• Якщо 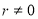  , то число  q називають неповною часткою. Число r називають остачею.

Наприклад:  Для чисел а=2, b=7 існує пара q=0 і r=2, тобто 2=7·0+2.

 Для чисел а=-2, b=5 існує пара q=-1 і r=3, тобто  -2=5·(-1)+3.

 Для чисел а=-8, b=4 існує пара q=-2 і r=0, тобто -8=4·(-2)+0.

Для заданого натурального числа m, де m>1, множину Z можна розбити на m підмножин, які не перетинаються, таким чином, що першій підмножині належатимуть усі числа, які при діленні на m, дають в остачі 0.

Теорема: Якщо цілі числа а і b при діленні  на натуральне число m дають однакові остачі,  то .

Доведення: Нехай де . Тоді . Звідси .

Означення: Цілі числа a і b називають конгруентними за модулем m (mєN), якщо остачі при діленні їх на число m рівні.

                          - такий запис називають конгруенцією. Читають так:

“a конгруентне b  за модулем m”.

Наприклад, , , , .

Теорема: Для того, щоб цілі числа a і b були конгруентними за модулем m, (mєN),  необхідно й достатньо, щоб різниця a-b ділилася націло на m.

3. Розв’язування вправ

 - вправа «Я знаю…» (учні за бажанням розв’язують вправи біля дошки)

1. Знайдіть неповну частку і остачу при діленні числа a на число b, якщо:

           1) a=253, b=19;    3) a=-26, b=3;   

           2) a=8, b=13;        4) a=-1, b=7.

2.  Які остачі можна отримати при діленні цілого числа на 7?

3.  Дано множини A, B, X, які попарно не перетинаються, і A B X =Z. Знайдіть  множину Х, якщо А = , B = .

4. Яку остачу при діленні на 3 дає число виду 3k-2, де k Z?

5. Відомо, що при діленні числа m на 18 остача дорівнює 11. Знайдіть остачу при діленні числа m: 1)на 2; 2)на 3; 3)на 6;4)на 9.

6. Число m кратне 6. Чому може дорівнювати остача при діленні числа m на 18?

7. Числа a при діленні на 6 дає в остачі 3, а при діленні на 4 дає в остачі 1.          Знайдіть остачу при діленні числа a на 12.

8. Число m дає рівні остачі при діленні на 3 і на 4. Чому може дорівнювати остача при діленні  числа m на 12?

9. Замість знака   запишіть таке найменше невід’ємне число, щоб отримана конгруенція була  правильною:

         1) 56 (mod 8);                      4) 3(mod 15);

         2) 23 (mod 7);                      5) -2(mod 18);

         3) -43 (mod 5);                     6) 6(mod 2);

10.  Відомо, що а -11(mod 8), b -2(mod 8). Знайдіть остачу при діленні на 8 числа:    1) a+b;  2) a-b;  3) 2a-3b;  4) ab; 5) a²;  6) b³.

4. Домашня робота

1)  Знайдіть неповну частку і остачу при діленні числа m на число n, якщо:

           1) m=9, n=15;   2) m=-31, n=10;       3) m=-6, n=11.

2) Задайте всі множини, кожна з яких складається з усіх цілих чисел, які мають 

           однакові остачі при діленні на 4.

3) Яку остачу при діленні на 6 дає число виду 6n-1, де n Z?

4) Відомо, що при діленні числа n на 16 остача дорівнює 9.

         Знайдіть остачу при діленні числа n: 1)на 2; 2)на 4; 3)на 8.

5) Число n кратне 4. Чому може дорівнювати остача при діленні числа n на 16?

6) Числа b при діленні на 5 дає в остачі 2, а при діленні на 3 дає в остачі 1.

     Знайдіть остачу при діленні числа b на 15.

7) Замість знака   запишіть таке найменше невід’ємне число, щоб отримана конгруенція була   правильною:

 1) 84 (mod 9); 2) -26 (mod 6);      3) -3(mod 11);

8) Відомо, що а -4(mod 6), b -9(mod 6). Знайдіть остачу при діленні на 6 числа:     1) 3a+4b;  2) a²-b;  3) b²+ ba.

Використані джерела:

1. Алгебра підручник для 8 класу з поглибленим вивченням математики,

А.Г. Мерзляк,  В.Б. Полонський, М.С. Якір, - Харків, «Гімназія», - 2009

2. Алгебра та початки аналізу 10 клас, профільний рівень

А.Г. Мерзляк, Д.А. Номіровський,  В.Б. Полонський, М.С. Якір, - Харків «Гімназія», - 2010

3. О.Ю. Карік, Матеріали для факультативних занять, спецкурсів, гуртків, математика 5-7, Харків, - «Основа», -  2008