Урок "Тотожні перетворення виразів, що містять квадратні корені"

Тема: Тотожні перетворення виразів, що містять квадратні корені

Мета:

• сформувати вміння виконувати тотожні перетворення виразів, що містять квадратні корені, зокрема виносити множник з-під знака кореня, скорочувати дроби, звільнятися від ірраціональності в знаменнику дробу;
•  розвивати логічне мислення, мову, вміння працювати самостійно, аналізувати ситуацію, оцінювати свої та дії інших;
• виховувати позитивні риси характеру: доброзичливість, взаємовиручку, справедливість, ставити мету та досягати успіху.

Тип уроку: засвоєння нових знань.

Обладнання: підручник, роздатковий матеріал.

Хід уроку:

І. Організаційний етап

II. Повідомлення теми та мети уроку. Мотивація навчальної діяльності

Cьогодні на уроці ми розглянемо тотожні перетворення виразів з коренями: додавання коренів, винесення множника з –під кореня, звільнення від ірраціональності в знаменнику дробу.

Бесіда:

«Чому необхідно уміти правильно виконувати тотожні перетворення виразів із квадратними коренями?»

 

Очікувана відповідь:

 Тому що застосування  тотожних перетворень зустрічається у геометрії при застосуванні теореми Піфагора, яку в свою чергу застосовують в будівництві та на місцевості, у фізиці для обчислення першої космічної швидкості та період математичного маятника.

Посміхнись! Ось такий він, справжній квадратний корінь, в житті! А Вам зустрічались такі дива?

 

III. Актуалізація опорних знань та вмінь

Гра – змагання «Математична естафета»

Клас поділений на дві команди. Учні по черзі виходять до дошки, розв’язують завдання, передають естафету іншому члену команди, самостійно обираючи порядок виконання завдань. Якщо хтось із команди помилився – потрібно виправити помилку та передати естафету іншому гравцю. Перемогу  здобуває та команда, яка виконала завдання найшвидше і отримала всі правильні відповіді.

Завдання для гри:

 

I команда	II команда
Знайдіть значення виразу:
Подайте у вигляді вираз:
Спростіть вираз:
3а + 2а + 5а;	(а + 2)(а + 3);
(а + 3)2	(а – 1)2 + 2а;

 

IV. Сприймання та усвідомлення нового навчального матеріалу

Фронтальна бесіда

• Множення та  ділення виразів, що містять квадратні корені

Використовуючи правила множення та ділення коренів, можна виконувати відповідні дії над виразами, що містять квадратні корені.

Приклад 1

:

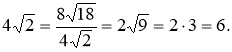
• Піднесення до степеня виразів, що містять квадратні корені

Використовуючи тотожність ()² = а, де а > 0 можна під­носити до степеня вирази, що містять квадратні корені.

Приклад 2

• Додавання квадратних коренів

Приклад 3

 

• Скорочення дробів

Приклад 4

 

• Звільнення від ірраціональності в знаменнику дробу

Приклад  5. Перетворити дріб  так, щоб він не містив  кореня у знаменнику дробу.

Розв'язання

Для виконання завдання досить чисель­ник і знаменник дробу помножити на :

 

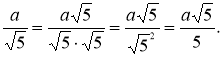
У такому випадку говорять, що ми звільнилися від ірраціо­нальності в знаменнику дробу.

Приклад 6. Звільнитися від ірраціональності у знамен­нику дробу .

Розв'язання

Помножимо чисельник і знаменник дробу на:

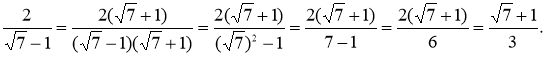
Отож, ми бачимо, що у кожного перетворення є свої особливості, їх треба знати. А знати краще будемо тільки тоді, коли більше будемо розв’язувати. Адже  «Уміє розв’язувати задачі той, хто їх розв’язує»

V. Осмислення та закріплення матеріалу

Робота з картками:

Учні з початковим і середнім рівнем навчальних досягнень самостійно виконують завдання за зразком на картках. Вчитель контролює роботу і при необхідності надає допомогу учням.

Прізвище, ім’я учня_________________________________________

 

1.Винести множник з-під знака кореня:

Зразок.

а)

б)

2.Внести множник під знак кореня:

а)
          б)

3.Звільнитись від ірраціональності в знаменнику дробу

Зразок.

а)

б)

4.Обчисліть:

 

а)

б)

5.Обчисліть:

а)

б)

6.Спростіть вираз:

7.Обчисліть:

   Зразок.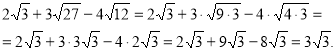

Робота біля дошки з коментуванням:

Учні з достатнім і високим рівнем навчальних досягнень  виконують вправи біля дошки

№ 1. Спростіть вираз   

№  2. Порівняйте числа і

№ 3. Скоротіть дріб:

     а)     б)     в)

№ 4. Звільніться від ірраціональності у знаменнику дробу:

     а)  б)  в)

№ 5. Обчисліть:

№ 6. Додаткове завдання

          Обчисліть: 

VI. Підсумок уроку

Вправа «Кореневий феєрверк»

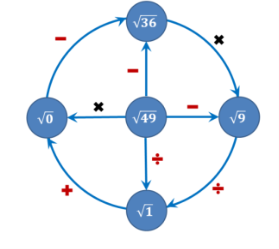Учні по черзі називають дії над коренями та їх результат. Передають естафету іншому гравцю.

 

 

 

 

 

VII.  Оцінювання навчальних досягнень

VІІІ.  Домашнє завдання

Опрацювати § 18, розв’язати завдання на картках

Поставтесь з відповідальністю до виконання домашнього завдання, оскільки з повторенням кожного правила, з виконанням кожного завдання ви наближаєтесь до досягнення мети – успішного написання контрольної роботи.

Вчіть свій розум та душу бачити хороше – і тоді дорога до успіху буде для вас відкрита.                      Завдання на картках

Достатній та високий рівні

Варіант 1

1.Спростіть вираз  

2. Скоротіть дріб:

     а)        б)

3.Звільніться від ірраціональності у знаменнику дробу:

     а)     б)     в).

4.Обчисліть:

       а)

      б)

Варіант 2

1.Спростіть вираз 

2. Скоротіть дріб:

     а)        б)

3. Звільніться від ірраціональності у знаменнику дробу:

 а)     б)     в).

4.Обчисліть:

       а)

      б)

Початковий і середній рівні

1.Винести множник з-під знака кореня:

 а)  б)

2.Внести множник під знак кореня:

а)   б)

3.Звільнитись від ірраціональності в знаменнику дробу

а)     б)

4.Обчисліть:

а)           б)

в)                       г)

д)