Урок "Тригонометрические неравенства"

Казахстан, ЗКО, г. Уральск

Уральский технологический колледж «Сервис»

Преподаватель Бурковская Нина Дмитриевна

Урок №32

Тема программы: 4. Тригонометрические функции -24 часа.

Тема урока: Решение тригонометрических неравенств

 Цель урока: показать алгоритм решения тригонометрических неравенств с использованием единичной окружности, научить решать простейшие тригонометрические неравенства, содействовать развитию математического мышления учащихся, побуждать учащихся к само-, взаимоконтролю, вызывать у них потребность в обосновании своих высказываний.

Тип урока: Совершенствования зун.

Методы ведения: Комбинированный урок.

Оборудование урока Тригонометрические формулы

ХОД УРОКА:

Организационный момент – 1 – 2 мин.

1. Приветствие учащихся.
2. Отметить отсутствующих.

II.      Опрос по домашнему заданию

III.   Объяснение нового материала. Краткий конспект.

Определение :

Простейшими тригонометрическими неравенствами называют неравенства вида

Неравенства : sin x > a, sin x≥  a, sin x < a, sin x ≤ a

Sin x > a,  arcsin a + 2π n < x < – arcsin a + 2π n, n Z

ά = arcsin a; ά = π  – arcsin a.

sin x<a  – π– arcsin a + 2π n<x< arcsin a + 2π  n, n  Z

ά = –π  – arcsin a ; β = arcsin a.

В случае нестрогих неравенств знаки < и > в решениях заменяются соответственно на ≤  и ≥.

Неравенства : cos x > a, cos x≥  a, cos x < a, cos x ≤ a.

cos x > a,   -arccos a+2π n <x< arccos a+2π n, n Z

ά =   – arcсos a ; β = arcсоs a

cos x <  a,   arccos a+2π n <x< 2π - arccos a+2π n, n Z

ά =   – arcсos a ; β = arcсоs a

Алгоритм решения тригонометрических неравенств с помощью единичной окружности:

1. На оси, соответствующей заданной тригонометрической функции, отметить данное числовое значение этой функции.

2. Провести через отмеченную точку прямую, пересекающую единичную окружность.

3. Выделить точки пересечения прямой и окружности с учетом строгого или нестрогого знака неравенства.

4. Выделить дугу окружности, на которой расположены решения неравенства.

5. Определить значения углов в начальной и конечной точках дуги окружности.

6. Записать решение неравенства с учетом периодичности заданной тригонометрической функции.

Формулы решения простейших тригонометрических неравенст:

1. sinx>a (|a|<1)      x∈(arcsin(a)+2Rπ; π-arcsin(a)+2Rπ)

2. sinx≥a (|a|<1)      x∈[arcsin(a)+2Rπ; π-arcsin(a)+2Rπ]

3.  sin<a (|a|<1)        x∈(-π-arcsin(a)+2Rπ; arcsin(a)+2Rπ)

4. sin≤a (|a|<1)        x∈[-π-arcsin(a)+2Rπ; arcsin(a)+2Rπ]

5.  cosx>a (|a|<1)     x∈(-arccos(a)+2Rπ; arccos(a)+2Rπ)

6. cosx≥a (|a|<1)     x∈[-arccos(a)+2Rπ; arccos(a)+2Rπ]

7. cosx<a (|a|<1)      x∈(arccos(a)+2Rπ; 2π-arccos(a)+2Rπ)

8. cosx≤a (|a|<1)      x∈[arccos(a)+2Rπ; 2π-arccos(a)+2Rπ]

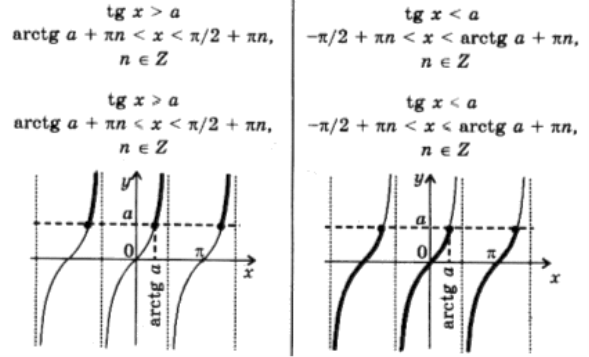
9.  tgx>a                   x∈(arctg(a)+Rπ; (π/2)+Rπ)

10.  tgx≥a                 x∈[arctg(a)+Rπ; (π/2)+Rπ)

11.  tgx<a                 x∈((-π/2)+Rπ; arctg(a)+Rπ)

12. .  tgx≤a                x∈((-π/2)+Rπ; arctg(a)+Rπ]

13.  ctg>a                  x∈(Rπ; arcctg(a)+Rπ)

14. ctg≥a                  x∈(Rπ; arcctg(a)+Rπ]

15.  ctg<a                x∈(arcctg(a)+Rπ; π+Rπ)

16. ctg≤a                x∈[arcctg(a)+Rπ; π+Rπ)

Закрепление нового материала: № 136,138

Задание на дом §11№137

Литература:  А.Е. Абылкасымова и др. Алгебра и начала анализа 10, 11 классы.

Ж. Кайдасов, В. Гусев, А Кагазбаева Геометрия 10, 11 классы. Дидактический материал по алгебре и начала анализа для 10, 11 класов.