урок Тригонометричні функції. Тригонометричні формули. Розв'язування вправ.

Тернопільська ЗОШ № 4

 

 

 

 

Розробка

відкритого уроку за темою:

«Тригонометричні функції. Тригонометричні формули. Розв’язування вправ.»

 

 

 

 

Підготувала:

вчитель математики

Дудник О. В.

 

 

 

 

 

м. Тернопіль,  2022р.

Девіз уроку:

«Розум полягає не тільки в знанні, але й в умінні застосовувати знання на практиці»

Давньогрецький філософ Аристотель

Тема уроку:  Тригонометричні функції. Тригонометричні формули. Розв’язування вправ.

 

Мета уроку:

•     Навчальна: вдосконалити та перевірити знання учнів з теми; розвивати вміння виконувати перетворення виразів, використовуючи основні співвідношення тригонометричних функцій числового аргументу, тригонометричних формул та формул зведення. Систематизувати знання учнів з метою всебічного осмислення ними даної теми.

 

 

•     Виховна: виховувати інтерес до вивчення математики, потяг до наукової творчості, уявлення про математику як невід’ємну складову загальнолюдської культури. Привчати до вміння спілкуватися та вислуховувати інших.

 

•     Розвиваюча: сприяти розвитку умінь та навичок щодо розв’язання вправ на застосування тригонометричних формул; інтелектуальних і творчих здібностей учнів; розвивати математичну мову та логічне мислення; розширювати кругозір; вміння працювати в колективі.

 

 

 

Очікувані результати:

•        Учні повинні засвоїти тригонометричні функції числового аргументу; основні тригонометричні формули; формули зведення.
•        Вміти використовувати набуті знання при розв’язуванні різнорівневих завдань.
•        Засвоїти навички виконання завдань на швидкість, індивідуальної самостійної роботи та роботи в групах.
•        Вміти висловлювати власні думки.

 

Обладнання:

 підручники, дидактичний матеріал, комп’ютерні технології, картки самооцінювання.

 

Тип уроку: повторення, узагальнення і систематизація знань з вивченої теми.

 

Формувати ключові компетентності:

- компетентність уміння вчитися:

  виконувати розумові операції й практичні дії;

- загальнокультурна компетентність:

  культура міжособистісних відносин;

• інформаційно – комунікативну компетентність:

уміння здобувати нові знання на основі наявних;

уміння формувати власну точку зору й доводити власну позицію;

• здоровʼязбережувальна компетентність:

уміння долати труднощі

Формування компетентностей:

✵ предметна компетентність: домогтися засвоєння формул  для тригонометричних функцій; сформувати вміння застосовувати ці формули до перетворення виразів;

ключові компетентності:

✵ спілкування державною мовою — аргументувати, доводити правильність тверджень;

✵ уміння вчитися впродовж життя —відбирати й застосовувати потрібні знання та способи діяльності для досягнення  мети;

✵ соціальна та громадянська компетентності — співпрацювати в команді, виділяти та виконувати власну роль у командній роботі;

 

 

Хід уроку:

1. Організаційний момент (1 хв.)

Оголошення теми й мети уроку. Запишемо в зошитах тему уроку

Вправа «Побажай успіху!»

• Прошу вас повернутись до сусіда, побажати гарного настрою, творчих успіхів та продуктивної роботи на уроці.

 

Підпишіть Картку самооцінювання        (не забувайте, що ми працюємо на довірі )

 

ПІ_____________________________________

 

Види роботи на уроці	Бали
Усні вправи (+12)
Домашнє завдання (+12)
Захист проектів (+12)
Робота в групах ( +12)
Тести (+12)
Загальна сума балів

 

 

2. Мотивація навчальної діяльності учнів.

 

 Систематизувати знання учнів з метою всебічного осмислення ними даної теми.

Виховувати уявлення про математику як невід’ємну складову загальнолюдської культури.

 Розвивати  кругозір; вміння працювати в колективі.

Формування компетентностей:

✵ предметна компетентність: домогтися засвоєння формул  для тригонометричних функцій; сформувати вміння застосовувати ці формули для перетворення виразів;

ключові компетентності:

✵ спілкування державною мовою — аргументувати, доводити правильність тверджень;

✵ уміння вчитися впродовж життя —відбирати й застосовувати потрібні знання та способи діяльності для досягнення  мети;

✵ соціальна та громадянська компетентності — співпрацювати в команді, виділяти та виконувати власну роль у командній роботі;

 

3 Актуалізація опорних знань (3 хв.).

Усні вправи

Запитання 1

cos² α + sin² α = ?

Запитання 2

tgα ×ctgα=

Запитання 3

Встановіть знак виразу sin210^о

Запитання 4

Установіть відповідність між градусними мірами кута та їх радіанним значенням:

1. 180⁰

2. 60⁰

3. 270⁰

4. 20⁰

A)

Б) 2П

В)

Г)

Д ) П

Запитання 5

Установіть відповідність між чвертями та кутами, які їм належать:

1. І

2. ІІ

3. ІІІ

4. ІV

А) 2П

Б)

В) -

Г)

Д)

Запитання 6

Спростіть вираз sinα⋅ctgα .

Запитання 7

Спростіть вираз tg² β(1− sin² β)

Запитання 8

Обчислити sin 225⁰

Запитання 9

Спростити вираз (1 - sin²β) : (1 - cos²β)

Запитання 10

1-sin²α-cos²α=

Запитання 11

Обчисліть cos 0⁰ + tg 45⁰ – 4 sin 30^{0 =}

Запитання 12

 

Відповіді

1. cos² α + sin² α = 1

2. tgα ×ctgα=1

3.Встановіть знак виразу sin210^о

-

4. Установіть відповідність між градусними мірами кута та їх радіанним значенням:

1. 180⁰

2. 60⁰

3. 270⁰

4. 20⁰

A)

Б) 2П

В)

Г)

Д ) П

1Д, 2В, 3Г, 4А

5. Установіть відповідність між чвертями та кутами, які їм належать:

1. І

2. ІІ

3. ІІІ

4. ІV

А) 2П

Б)

В) -

Г)

Д)

1Г, 2Б, 3Д, 4В

6. Спростіть вираз sinα⋅ctgα =Cosa

7. Спростіть вираз tg² β(1− sin² β)=sin² β

8. Обчислити sin 225⁰ = -√2/2

9. Спростити вираз (1 - sin²β) : (1 - cos²β)=ctg²β

10. 1-sin²α-cos²α=0

11. Обчисліть cos 0⁰ + tg 45⁰ - 4sin 30^{0 =}0

12.  = cos² α

4. Перевірка домашнього завдання

13.4 1) cos 6a  cos 2a – sin 6a sin 2a = cos(6a + 2a) = cos 8a;

2)  sin 12 cos 18 + sin 18  cos 12 =  sin ( 18  + 12) = sin 30 = ;

3)  sin (- 15) cos 75 + cos 15 sin 75 =  cos 15 sin 75 - sin 15 cos 75  =  

 sin ( 75 – 15 ) = sin 60 = ;

4) cos (a – b) - 2 sina sinb =  cosa cos b + sina sinb  - 2 sina sinb =  cosa cos b -  sina sinb = cos (a + b).

 

14.4   1) sin ( - 305 ) = - sin 305 = - sin ( 270 + 35) = - ( - cos 35) = cos 35;

2)  sin = sin ( П - )= sin ;

3) cos ( - 0,7 П) = cos 0,7 П = cos ( П – 0,3 П) = - cos  0,3 П;

4) cos  = cos ( П + ) =  - cos   .

14.6 1) cos ( - 150) = cos 150 = cos  ( 180 - 30) = - cos 30 = - ;

2) cos 210 = cos  ( 180 + 30) =  - cos 30 = - ;

3) sin 315 = sin ( 270 + 45 ) =  - cos 45 = - ;

4)  sin (- ) = - sin = - sin (2П - ) = - ( -  sin  ) =  sin = .

 

 

5. Захист проектів.

  Частина 1.    Історична  довідка

Частина 2.    Тригонометрія в нашому житті

 

6. Руханка

 

7. Вдосконалення вмінь, відпрацювання навичок

 

 Практична робота в групах

Письмові вправи

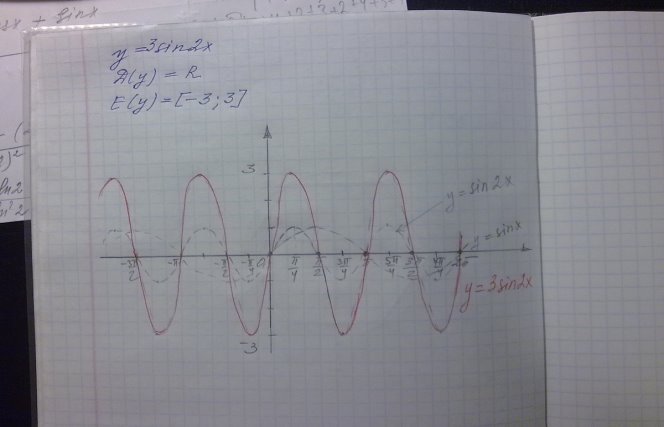
1) Побудувати графік функції y=3 sin (2x).

 

 

 

 

 

 

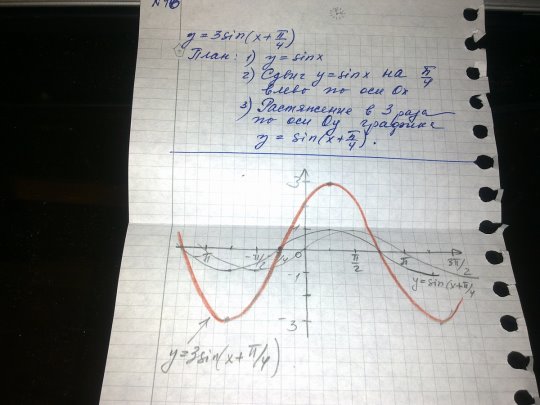
2) Побудувати графік функції y=3 sin (x + ).

 

 

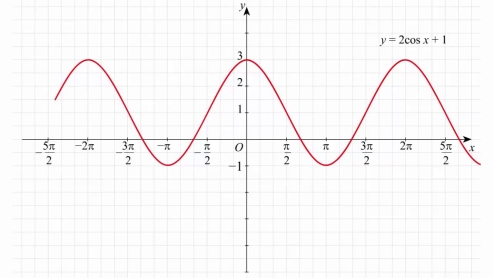
y=2cosx + 1

 

Тригонометричні функції числового аргументу. Радіанне вимірювання кутів   

                                                                  І в

 

 

Побудувати графік функції y=3 sin (2x).

 

 

1. Знайти значення виразу:  1)           2) tg

 

2. Визначити знак рівності

а)     б)

 

 

3. Порівняти : а)       б)

 

 

4. Кутом якої чверті є кут, радіанна міра якого 3,5 радіана?

       A) І                  Б) ІІ              В)ІІІ                    Г) ІV

 

5. Знайдіть , якщо  ,   .

      A) 0,2                  Б) -0,6             В)-0,2                   Г) 0,6

 

6. Знайдіть значення виразу

 

 

 

 

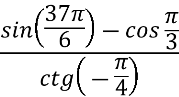
Тригонометричні функції числового аргументу. Радіанне вимірювання кутів   

                                                                 ІІ в

 

 

Побудувати графік функції  y=3 sin (x + ).

 

 

 

1. Знайти значення виразу: 1)      1)   

 

2. Визначити знак рівності

а)     б)

 

3. Порівняти : а)       б)

 

 

4. Кутом якої чверті є кут, радіанна міра якого 7,3 радіана?

       A) І                  Б) ІІ              В)ІІІ                    Г) ІV

 

 

5. Знайдіть значення виразу

 

 

6. Знайдіть , якщо  ,   .

      A) 0,2                     Б) -0,6               В)-0,2             Г) 0,6

 

 

 

 

                                                               IІІ в

Побудувати графік функції  y=2cosx + 1

 

 

 

1. Знайти значення виразу: 1)      1)   

 

2. Визначити знак рівності

а)     б)

 

3. Порівняти : а)       б)

 

4. Кутом якої чверті є кут, радіанна міра якого  4,3 радіана?

       A) І                  Б) ІІ              В)ІІІ                    Г) ІV

 

 

5. Знайдіть значення виразу

 

                                                        

 

6. Знайдіть , якщо  ,  0.

      A)                    Б)                 В)                 Г)

 

Відповіді:

                                                                  І в

 

1. Знайти значення виразу: 

1)    =  +   

  2) tg = 1 - =

2. Визначити знак рівності

а)    +  -  + < 0

                                                       1 2  3

   б) -  -  + 0

                                                        2  3  1

 

3. Порівняти : а)    

  б)

 

4. Кутом якої чверті є кут, радіанна міра якого 3,5 радіана?

       A) І                  Б) ІІ              В)ІІІ                    Г) ІV

 

3,5 радіан =3,5 * 57 =199,5   3 чверть  В

 

5. Знайдіть , якщо  ,   .

      A) 0,2                  Б) -0,6             В)-0,2                   Г) 0,6

 

=  - 0,6  Б

 

6. Знайдіть значення виразу

 

  = = 0

ІІ в

1. Знайти значення виразу:

1) = 1 - = 

 

    2)    =   +

 

2. Визначити знак рівності

а) +  -  + < 0

                                                    1  3  3

   б) +  -  - 0

                                                1 3 3

 

3. Порівняти : а)

 

    б)

 

4. Кутом якої чверті є кут, радіанна міра якого 7,3 радіана?

       A) І                  Б) ІІ              В)ІІІ                    Г) ІV

 

7,3 * 57 = 416,1         A) І

   

4. Знайдіть значення виразу

 

  = = ;

6. Знайдіть , якщо  ,   .

      A) 0,2                     Б) -0,6               В)-0,2             Г) 0,6

=  - 0,6  Б

                                                               IІІ в

1. Знайти значення виразу: 1) = 1 - = ;

    2)    = 1 +   = 1,5 .

 

2. Визначити знак рівності

а)  +  -  - 0

                                                     1 2 2

   б) +  +  - < 0

                                                       1 2 2

3. Порівняти : а) ; 

   б) ;

 

4. Кутом якої чверті є кут, радіанна міра якого  4,3 радіана?

       A) І                  Б) ІІ             В)ІІІ                    Г) ІV

4,3 * 57 = 245, 1  В)ІІІ 

 

5.   Знайдіть значення виразу

 

                          = =0;

6. Знайдіть , якщо  ,  0.

      A)                    Б)                 В)                 Г)

 

      A)                   

     

- 0,6  Б1111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111118. Узагальнення знань

Тести (самоперевірка).

Тест :Тригонометричні функції

1.Знайдіть значення виразу :    -2cos60 + sin30⋅ tg135

а)1,5

 б)2

 в)-2

 г)-1,5

2.Укажіть радіанну кута 225° ?

а)

 б)

 в) 

 г) 

3.Укажіть градусну міру кута ?

а)150

 б)270

 в)60

 г)225

4.Обчисліть : 2cos(-α) -2sin ( + α)

а)0

 б)1

 в)-2

 г)2

5.Обчичліть : sin94cos49 - sin49cos94

а)

 б)1

 в)-2

 г)  

Відповіді до тесту:

1.  г) -1,5

2.  а) 

3.  а)150

4.  а)0

5.   г)

9. Підсумки уроку.

 Оголошення оцінок

Картка самооцінювання

ПІ_____________________________________

 

Види роботи на уроці	Бали
Усні вправи (+12)
Домашнє завдання (+12)
Захист проектів (+12)
Робота в групах ( +12)
Тести (+12)
Загальна сума балів

 Пояснення домашнього завдання

Запишіть, будь-ласка, домашнє завдання

Прочитати пункт 13, 14, ст. 76, 82, вивчити означення, формули, розв'язати № 13.6, 14.8, |високий рівень14.10.

Рефлексія.

Інтерактивна вправа “Коло вільних думок”

Як Ви вважаєте, чи досягли ми мети уроку?

Що нового Ви дізнались?

Чи все було зрозуміло?

Що сьогодні виконували на уроці?

Що зрозумів?

Що було цікавим?

Що буде корисним в житті?

На розвиток яких рис характеру вплинув урок?

 

 

СМАЙЛИКИ

 

 

Урок закінчено.  Дякую за увагу!