Урок " Тригонометрія: вчити чи не вчити"

Тригонометрія: вчити чи не вчити?

 

                           Зима за літом, ніч за днем. Плюс змінюється мінусом.

                           Все у природі і в людей йде за законом синуса.

                           То вверх крокуємо, то вниз, удачі за невдачами,                             По синусоїді кудись всі пливемо неначе ми.

 

Розділ: наука, природа, мистецтво.

Рівень: 10-11 клас

Тема: наука

Мета: Дізнатися, що таке тригонометрія, де тригонометричні функції зустрічаються в математиці, природі, де і як використовуються у нашому житті.

 

Яка інформація мене тут чекає:

ØЩо таке тригонометрія

ØЯкі тригонометричні функції вивчають математики

Ø

Де зустрічається тригонометрія у природі та житті

ØЯку роль зіграла тригонометрія у розвитку астрономії

 

                          

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                            

 

Що таке тригонометрія і як вона виникла? Яку роль відіграє тригонометрія в фізиці, природі, біології, медицині?        Чому          знання        тригонометрії потрібні сучасній людині?                За допомогою  тригонометрії з давніх часів люди          вивчали відстані. Тригонометрія (з         грецької     trigoonтрикутник, metro-метрія) – розділ математики, в якому вивчаються залежності між величинами кутів та довжинами сторін трикутників, алгебраїчні тотожності тригонометричних       функцій.     За допомогою до недосяжних предметів, складали

географічні карти, здійснювали виміри землі та розрахунки у будівництві. Початок тригонометрії як вчення було покладено в Індії. Головним досягненням індійських астрономів стала заміна хорд синусами, що дозволило вводити різні функції, що мають відношення до сторін і кутів прямокутного трикутника. Тригонометрія сучасності стала заслугою Леонарда Ейлера. Визначення терміну « тригонометричні функції» надається у його        трактаті «Введення в        аналіз нескінченних»(1748). Протягом довгого часу тригонометрія     вивчалася   і розвивалася       як      один з        розділів астрономії. На будь-якій кулі, як і на

поверхні Землі, відстані між точками можна розрахувати за кутами, під якими її видно з центра кулі. Задачу про знаходження усіх елементів сферичних трикутників розв’язав Франсуа Вієт. 

Тригонометрія пройшла довгий шлях розвитку і тепер ми можемо впевнено сказати, що тригонометрія не залежить від інших наук, а інші науки залежать від тригонометрії. Починаємо цікаву подорож у світ тригонометрії!

 

 

                       

 

 Згадаємо, що таке синус, косинус, тангенс, котангенс гострого кута прямокутного трикутника. Навіщо ми це вивчали? Для яких кутів мали місце вивчені поняття?

 

 

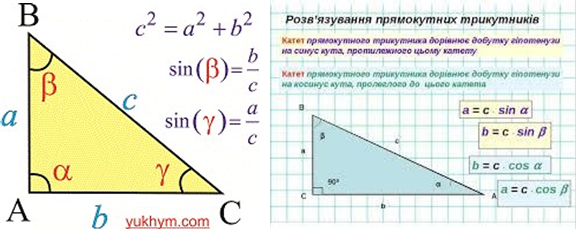
А чи бувають тригонометричні функції кутів, більших за 90 градусів?

 

 

 

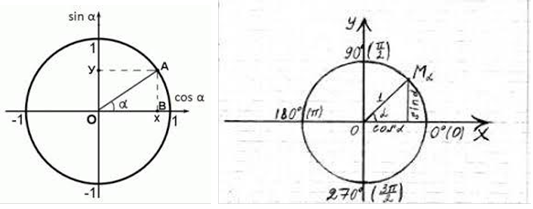
Що ви бачите на малюнку?

Які формули тригонометрії ми вивчили?

 

Усе так складно? А навіщо?

 

 

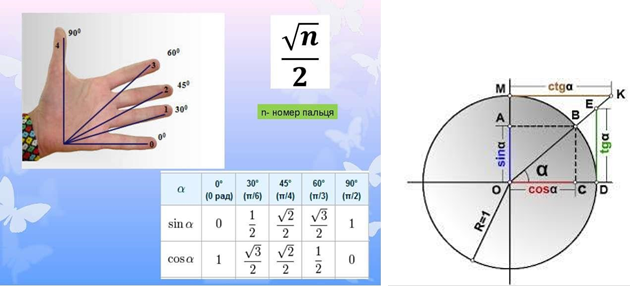
Завдання:  

1) 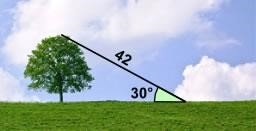    розв’язати задачу  

  

 

 

 

 

2) 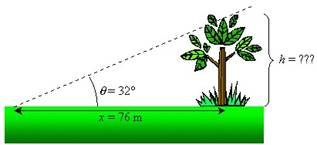    розв’язати задачу  

 

 

 

 

 

 

3)     Cпростити вираз:

1) 1-cos²a                                   2)  cos²a+(1-sin²a)

3) sin²a-1                                   4) sin²a+2 cos²a-1

5) cos²a+ sin²a+tg²a                 6) 1- sin²a- cos²a 

 7 ) cos²a –( 1+2 sin²a)             8) tga ctga+ctg²a

 9) - sin²a- cos²a                       10)  1- sin²a +1- cos²a

 11) tgactga+1                          12) ctgasina+1

Відповіді:  cos²a;  1/ cos²a;  - cos²a;  2 cos²a;  сosa+1;  0;  -1;  1;  2;  sin²a;  1/ sin²a;  -3/ sin²a.

          

                                  

                               Щасливий той, хто в звичнім наче побачив  те, чого ніхто не бачив.

                                                                    Дж.Г.Байрон

 

Коли ми дивимося на графіки тригонометричних функцій, то можемо згадати, що є схожі криві в нашому житті. Наприклад, хвилі на морі мають форму, що нагадує синусоїду.

У світі, що нас оточує, ми зустрічаємося з періодичними процесами, що повторюються через однакові проміжки часу. Ці процеси називають коливальними. Коливальні явища різної фізичної природи підкоряються загальним

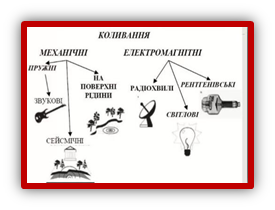закономірностям і         описуються         однаковими рівняннями. 

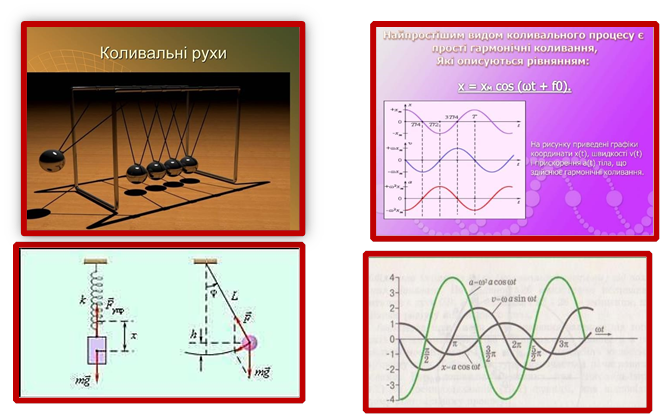
Коливання – найпоширеніша форма руху в оточуючому нас світі та техніці. Коливаються хвилі, дерева під дією вітру, поршні автомобілів і т.п. Прикладами простих коливань можуть слугувати вантаж на пружині або математичний маятник. Коливання, при яких змінення фізичних величин відбуваються за законами косинуса або

синуса, називають гармонічними коливаннями

 

Механічні коливання                                       Гармонічні коливання

 

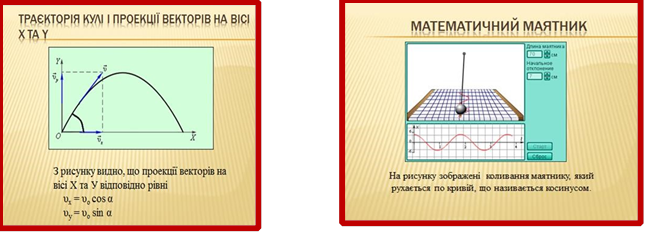
Як виникла веселка? Північне сяйво? За яким графіком рухається Сонце? Як тригонометрія допомогає  знайти відповіді на ці запитання? 

 

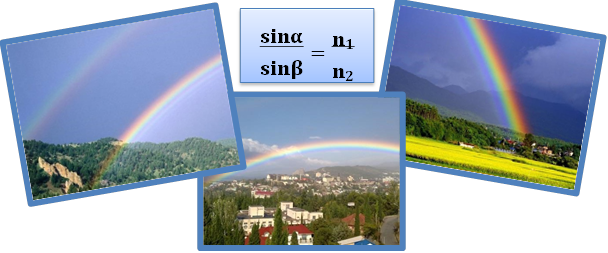
Вперше теорія веселки була дана у 1637 Рене Декартом, який пояснив веселку як явище, пов’язане з відображенням і заломленням світла в дощових краплях.

Що таке Північне сяйво? У верхні шари атмосфери Землі проникають частинки сонячного вітру і взаємодіють з магнітним полем планети.

Завдання:

1.                 На похилій площині, яка складає з горизонтом кут 24,5⁰, знаходиться тіло масою 90 кг. Знайдіть, з якою силою воно скотиться по похилій площині і який тиск воно справляє на цю площину .

 

2.                 Сили в 40 Н і 56 Н діють на одну і ту ж точку тіла під прямим кутом.  Знайдіть рівнодіючу цих сил і кути , утворені нею з кожної зі складових .

 

3.                 За допомогою відривного календаря побудуйте графіки  сходу та заходу Сонця за даними на перше число кожного місяця протягом року. Вісь ОУ – час сходу (заходу) Сонця, вісь ОХ – місяць року.

 

У давнину люди спостерігали за рухом небесних тіл. За зірками визначали положення кораблів в морі або напрямок руху каравану в пустелі. Вчені обробляли дані вимірів, щоб вести календар і правильно визначати час початку сівби і збору врожаю, дати релігійних свят.

  

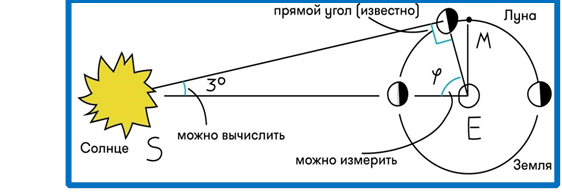
при відомому значенні одного з кутів. Аристарх розглядав

прямокутний трикутник, що утворено Сонцем, Луною та Землею під час квадратури.

Складені Гіппархом ( бл.190 до н.е. – бл. 120 до н.е.) таблиці розташування Сонця і Луни дозволили       обчислювати       моменти,    коли відбуваються затемнення ( з похибкою 1-2 години). Гіппарх вперше став використовувати в астрономії методи сферичної геометрії. Він підвищив точність спостережень, застосувавши

для наведення на об’єкт хрест нитей в кутомірних приладах – сектантах і квадрантах. Вчений склав величезний за тими часами каталог положень 580 зірок, поділивши їх за блиском на 6 ступенів (зоряних величин). Гіппарх ввів географічні координати широту та довготу, його можна вважати засновником математичної географії.

          Пізніше Клавдій Птоломей  у своїх працях « Географія», «Аналемма»,       «Планісферій»    надає докладні застосування тригонометрії в картографії, астрономії та механіці. В « Альмагесті» він наводить таблицю довжин хорд кола радіусом в 60 одиниць, обчислених з кроком 0,5 градуса з точністю до 5 десяткових знаків включно. Праця Птоломея була декілька століть введенням в тригонометрію для астрономів. 

Тригонометрія використовувалася для:

Ø Точного визначення часу в сутках

ØОбчислення розташування небесних світил, моменти їх появи та заходу, затемнення Луни та Сонця

ØВизначення географічних координат місця знаходження

ØОбчислення відстані між містами, якщо відомі їх географічні координати.

 У 4-5 століттях  в працях з астрономії  великого індійського вченого Аріабхати  виник термін sinus.

Слово косинус набагато молодше. Косинус – це скорочення від латинського виразу completeby sinus, тобто «додатковий синус», cosa=sin(90-a). Назва тангенс походить від латинського tanger (дотикатися) і з’явилася у 1583 році. Подальший розвиток тригонометрія получила в працях астрономів Ніколая Коперника (14731543), Тихо Браге (1546-1601), Йогана Кеплера (1571-1630) і Франсуа Вієта (15401603).

Як рухаються планети? Чому у нас чотири пори року? Який шлях проходить Сонце від сходу до заходу?

                    Велика книга природи написана мовою математики.

                                                                               Галілео Галілей

 

Яке відношення має тригонометрія до природи? Як відбуваються рухи у тваринному світі? Дивно, але за законом синуса. Крила птахів, хвости риб, тіло змії, рухаючись, відтворюють графік синусоїди.

                            

Медицина і математика. Що може бути спільного? Усім знайомі слово «електрокардіограма» і крива, що описує електричну активність серця. Електричний струм виникає і розповсюджується по всьому організму при кожному скороченні серця.У результаті досліджень студента іранського університету Ширази Аббасі була створена формула, яка полегшує процес опису основних параметрів діяльності серця, прискорюючи тим самим постановку діагнозу  і початок лікування. Ця формула є комплексне алгебраїчно-

тригонометричне рівняння, що складається з 8

виразів, 32 коефіцієнтів і 33 основних параметрів, включаючи кілька додаткових для розрахунків  у випадках аритмії.

Зв'язок з тригонометрією мають інтелект, емоції та фізичний людини, які є періодичними процесами. Кожна людина поєднує в собі набір різних біоритмів: інтелектуальний,

емоційний та фізичний, які

стартують одночасно в момент народження і відразу починають

рости, потім зменшуються, потім знову ростуть, періодично повертаючись до початкового значення. Зміни біоритмів відбуваються періодично, але не синхронно.

Інтелектуальний ритм має період 33 дні і керує пам’яттю, здатністю до навчання, розумовою активністю.

Емоційний триває 28 днів, впливає на почуття, настрій, емоції. 

Фізичний ритм складає 23 дні і регулює фізичну активність, силу, швидкість, координацію, витривалість. 

В біології використовується таке поняття як сонний синус, каротидний синус і венозний або печерестий синус.

 

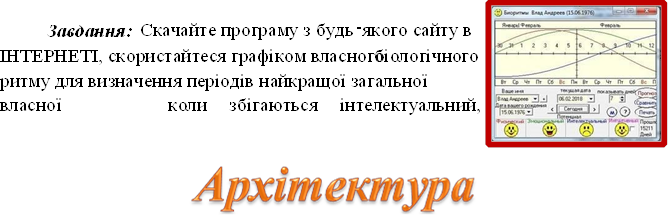форми,

емоційний та фізичний ритми.

 

                                     

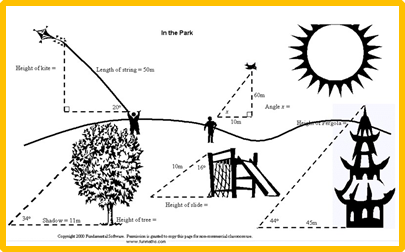Як це не дивно, але архітекторам, щоб створити неповторні будівлі, треба знати крім опору матеріалів, матеріалознавства та інших прикладних дисциплін, ще й тригонометрію. Але теоретичні знання вирішують не все. Ось що пригадують знавці про створення однієї з скульптур французького майстра Золотого століття мистецтва. Пропорційні співвідношення в побудові статуї були ідеальними. Однак при встановленні її на високий п’єдестал, статуя виглядала потворною. Скульптор не врахував, що в перспективі до горизонту зменшуються багато деталей і якщо дивитися знизу вверх, вже не складається враження її ідеальності. Проводилося багато розрахунків для того, щоб фігура і з висоти виглядала пропорційно. З’ясувалося,що знаючи відстань від статуї до точки зору, тобто від верху статуї до очей людини і висоту статуї, можна розрахувати синус кута       падіння      погляду за допомогою таблиць, таким чином буде знайдено точку зору. Ситуація змінюється, якщо статую піднімають на висоту, тому відстань від верхівки статуї         до      очей людини збільшується і синус кута падіння      теж збільшується.      Порівнюючи

виміри відстані від верхівки статуї до землі в першому і другому випадках, можна знайти коефіцієнт пропорційності. В подальшому створюється рисунок, а потім скульптура, яка буде наближена до ідеалу.

 

 

Завдання: Графіки яких функцій використовують архітектори у розрахунках об’єктів, зображених на фотографіях? 

 

Підведення  підсумків кейс-уроку.

№	Назва	Зміст
1	Результати уроку можна доповнити такими знахідками
2	Які три сайти допомогли знайти важливу інформацію	www.bibl.nngasu.ru/electronicresources/uchmetod/ecology/842968.pdf  https://ru.wikipedia.org/wiki/Тригонометрия https://sites.google.com/site/trigonometry121/trigonometria-vzizni
3	На допомогу учню і коучу	https://multiurok.ru/files/trigonometriia-v-realnoi-zhizniinformatsionnyi-pr.html  uchportfolio.ru/public_files/1215722342.ppt https://www.slideshare.net/rudenkoos/ss-57820978
4	Де знаходити інформацію для кейсу	https://kopilkaurokov.ru/.../trigonomietriia-i-ieie-primienieniiev-razlichnykh-sfierakh. https://nsportal.ru/ap/.../prezentatsiya-trigonometriya-vokruzhayushchem-nas-mire skverik.pro/it-is-interesting/the-history-of.../from-the-historyof-trigonometry/  https://vseosvita.ua › Бібліотека › Алгебра https://www.slideshare.net/rudenkoos/ss-57821666
5	Локація проведення кейсуроку	Кейс-урок проходить у класі
6	Змагання	За 3 хвилини записати як найбільше : 1) формул тригонометрії; 2)слів, використовуючи літери слова «тригонометрія»
7	Домашнє завдання	1) За допомогою відривного календаря побудуйте графіки  сходу та заходу Сонця за даними на перше число кожного місяця протягом року. Вісь ОУ – час сходу ( заходу) Сонця, вісь ОХ – місяць року. Скачайте програму з будь-якого сайту в ІНТЕРНЕТІ, скористайтеся графіком власного біологічного ритму для визначення періодів найкращої загальної власної форми, коли збігаються інтелектуальний, емоційний та фізичний ритми.
8	Тривалість	90 хвилин(спарений урок)
9	Можливість схеми заняття з учнем-дублером	Можливо
	Отримані знання і напрацьовані компетенції	Уміння швидко знайти необхідну інформацію і користуватися нею в практичних цілях Знання про застосування тригонометрії в математиці, фізиці, астрономії, медицині, природі, архітектурі Уміння конструювати нові знання на основі отриманих знань
		Тригонометричні функції, графіки, синус, косинус, тангенс, коливання гармонічні ,механічні, біоритми, е Електрокардіограма, сектант, квадрант, фази Луни, сход, захід Сонця, веселка, Північне сяйво, відстані, архітектурні форми.
12	Автори	Постнікова Тетяна Володимирівна, вчитель математики Марганецької спеціалізованої природничо-математичної школи І-ІІІ ступенів №11, вчитель вищої кваліфікаційної категорії, «Вчитель-методист»
13	Брали участь у апгрейді кейсу	Учні 10 класу Марганецької ПМШ №11