Урок "Трикутник та його елементи. Нерівність трикутника"

Тема: ТРИКУТНИК ТА ЙОГО ЕЛЕМЕНТИ. НЕРІВНІСТЬ ТРИКУТНИКІВ,

Мета: сформувати поняття трикутника як геометричної фігури; розглянути основні елементи трикутника; класифікувати трикутники за сторонами та кутами ; застосовувати отримані знання при розв’язуванні задач;

Розвивати просторову уяву та мислення. Виховувати захоплення математикою.

Тип уроку: засвоєння знань.

Обладнання: набір трикутників, презентація до уроку.

Хід уроку

І. Організаційний етап

ІІ. Актуалізація опорних знань і умінь учнів.

Фронтальна бесіда.

1.Які кути ви знаєте?

2.Що таке бісектриса кута?

3.За допомогою чого можна виміряти кут?

ІІІ. Мотивація навчальної діяльності учнів

Учням було задано випереджаюче домашнє завдання: спробувати з трьох кусків дроту скласти трикутник. Проаналізувати свої результати відповівши на запитання

1)Чи завжди можна скласти такі трикутник? Чому?

2)В яких випадках це неможливо?

Про це ми поговоримо сьогодні на уроці і з'ясуємо, коли саме такі трикутники існують, а коли ні.

IV. Засвоєння нових знань

План вивчення матеріалу

1.               Історична довідка про трикутник.

Трикутник – найпростіша фігура: має три вершини й три сторони.

Перші відомості про трикутник та його властивості ми знаходимо в єгипетських папірусах, яким більше 4000 років. У них згадується спосіб, яким знаходили площу рівнобедреного трикутника. Через 2000 років у Стародавній Греції високого рівня досягає вивчення властивостей трикутника

2.               Означення трикутника. 

Трикутник – це геометрична фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, що послідовно сполучають ці точки .

3.               Елементи трикутника: вершини, сторони, кути. 

Точки – це вершини трикутника, позначаються великими латинськими літерами А, В,С. Відрізки – це сторони трикутника. позначаються двома великими латинськими літерами АВ, ВС, СА, або однією маленькою а,в,с.

4.               Периметр трикутника. 

Периметр трикутника - це сума довжин всіх його сторін. P ABC = AB + BC + AC

5.               Види трикутників (за кутами, за сторонами). 

Залежно від міри кутів трикутники поділяються на види:гострокутні, прямокутні, тупокутні.

Залежно від довжини сторін трикутники поділяють на види: рівносторонні, різносторонні, рівнобедрені.

6.               Властивість сторін трикутника (нерівність трикутни­ка). 

Теорема:У будь-якому трикутнику кожна сторона менша за суму двох інших сторін (нерівність трикутника).

Наслідок.

А,В,С – довільні точки, які не лежать на одній прямій.

АВ < АС + ВС

АС < АВ + ВС

ВС < АВ + АС

V. Застосування нових знань.

Завдання 1

Василько та Дмитро вирішили виміряти розміри повітряного змія. Василько стверджує, що його розміри становлять 80см, 155 см і 80 см, а Дмитро – 70см, 155см і 70 см. Хто правий?

Задача 2

а)  Дано: ∆АВС. АВ = ВС, АВ = 4 см, АС на 3 см більша за АВ.

     Знайти : Р.

б) Дано: ∆АВС. АВ = ВС, АВ = 8 см, АС  в два рази менша  за АВ.

     Знайти : Р.

в)    Знайти сторони ∆АВС, якщо АВ : ВС : АС = 2 : 2 : 4, а периметр дорівнює 56 см.

Задача 2

Відстань від Донецька до Дніпропетровська становить 211 км, що на 12 км більше, аніж відстань між Донецьком та Запоріжжям. Яка відстань від Запоріжжя до Дніпропетровська, якщо периметр трикутника, утвореного цими містами, дорівнює 480 км?

Задача 3

Петрику потрібно обгородити грядку трикутної форми. Скільки йому необхідно метрів огорожі, якщо відомо, що сторони ділянки відносяться, як 4:5:8, а її периметр становить 34 м?

Задача 4

 Василько із куска дроту, довжиною 24см зігнув фігурку - рівносторонній трикутник. Який периметр цього трикутника? Яка довжина сторони?

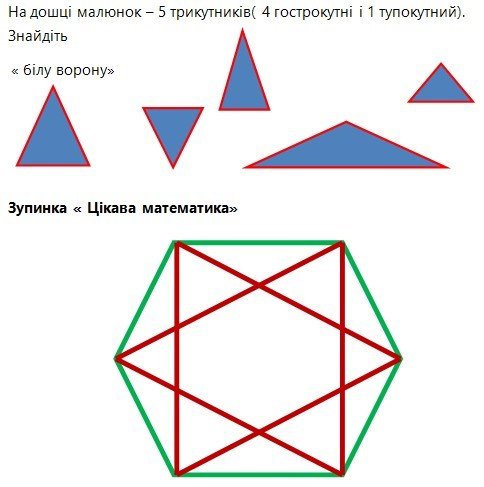
Відповідь: 32 трикутники.

V. Проведення практичної роботи.

Учням роздаються моделі трикутників. За допомогою  лінійки, косинця, транспортира визначити вид трикутника. Оформити роботу у вигляді таблиці.

VI. Підсумки уроку

Рефлексія 

•                   Сьогодні я на уроці …..
•                   Я дізнався…..
•                   Я поглибив……
•                   Мені нам уроці сподобалося…..
•                   Мене дуже здивувало…..
•                   Мене найбільше вразило….
•                   Я вирішив дізнатися більше про….
•                   Я вважаю дану тему…..
•                   Дані знання допоможуть мені під час…

VІI. Домашнє завдання 

1.               Опрацювати §3 п.16,    №368,    №391,    №415.
2.               Підготувати розповідь про трикутник у повсякденному житті

3.Задача з міжнародного математичного конкурсу кенгуру . Довжини двох сторін трикутника дорівнюють 5 см та 2 см, а довжина третьої дорівнює непарному числу сантиметрів. Чому дорівнює довжина третьої сторони?