Урок узагальнення і систематизації вивченого матеріалу з теми "Квадратична функція"

Тема: «Узагальнення і систематизація вивченого матеріалу з теми «Квадратична функція»

 

Мета:

• узагальнити і систематизувати знання учнів з теми «Квадратична функція»;
• формувати вміння коректно і доречно вживати математичну термінологію,здатність продуктивно співпрацювати в групі,

розвивати увагу учнів, логічне мислення, творчу активність;

• Сприяти самовихованню наполегливості,відповідальності

 

Тип уроку: Узагальнення і систематизація  знань, умінь і навичок,урок=ода.

 

Обладнання: комп’ютер з прикладним програмним забезпеченням, учительська презентація, роздатковий матеріал.

Хід уроку

 

 І.Організаційний етап.(1 хв) (слайд 1)

Учитель налаштовує учнів на роботу.

 Вправа «Ідеальне опитування»

          ІІ. Оголошення теми і мети уроку

             Розгадування ребуса (слайд 2)     

         Слухання вірша про відповідності

На цьому уроці нашим завданням буде систематизувати та узагальнити  ваші вміння будувати графіки функцій; щоб  підготуватися до контрольної роботи. (слайд 3,4 )

Отже, ви бачите, що дуже багато життєвих процесів у математиці описується за допомогою функцій. Завдання математики вивчити їх та спрогнозувати те, що буде відбуватися насправді, дивлячись на формулу, яка описує певний процес.

Сьогодні ми підіб’ємо підсумки вивчення теми «Квадратична функція, її графік і властивості». Я сподіваюсь на успішну працю, що на уроці ми зможете показати свої знання вміння, кмітливість, то ж будьте уважними, думайте, запитуйте, пропонуйте, оскільки нам разом з вами йти шляхом до  істини.

Підготуємо наші зошити до роботи. Пам’ятайте, що під час роботи з діловою документацією ,її треба вести старанно, охайно, уважно ставитися  до цієї справи.

Який малюнок відображає ваш настрій? (слайд 5)     

 ІІІ. Актуалізація опорних знань

 1.  Вправа «Інтелектуальна розминка» (слайд 6,7,8)     

1. Що називають функцією?
2. Що називають нулями функції?
3. Як, користуючись графіком функції у = х², побудувати графік функції: у=х² + 3; у = (х – 1)²;
4. у = (х – 1)² + 3; у = -х²?
5. Яку функцію називають квадратичною?
6. За якими формулами обчислюються координати вершини параболи?
7. Як визначити напрям віток параболи?
8. Як знайти  нулі квадратичної функції?

2.Усні вправи: гра «Поле чудес».

Цей етап уроку проходить у формі дидактичної гри «Поле чудес». На окремих аркушах умова завдань та аркуш з літерами. Відповіді до кожного завдання відповідає певна літера. Мета учнів скласти ключове слово.(Парабола)

1. Яка з наведених функцій є квадратичною?

      А) у = х – 1.   Б) у = – 1.   В) у = – 1.   Г) у = .

2. Знайти область визначення функції:

1. y = .

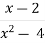3. Знайти множину значень функції   y = x² - 4x + 4.
4. Яка з точок (2;5), (-1;3) належить графіку функції f(x)= -2х² + 5 ?
5. Графік функції  y = 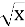перенесли паралельно вправо на 3 одиниці і на 4 одиниці вгору. Графік  якої функції було отримано?
6. Знайти нулі функції  y = x² - 2x – 8.

7.Указати проміжки зростання функції  y= (x + 3)².

(1; М	(- Б	y = + 4 А
0; 2 А	(- Е	Рисунок а) Р
у = – 1 Л	х=-5.х=0 П	(2 ; 11) Р
Рисунок г) О	[4; 12] А	y = + 4 И
[0; + Й	[1; + К	[-3; + Ц

 

 

 

1).Піднесіть

ІV. Удосконалення вмінь і навичок учнів.  

Отже, основні алгоритми ми з вами повторили, а тепер перевіримо, наскільки якісно ви засвоїли вивчений матеріал.          

 

 1.Математичний диктант.

1. Укажіть знак числа а.
2. Укажіть координати вершини параболи.
3. Знайдіть найбільше чи найменше значення функції.
4. Знайдіть нулі функції.
5. Укажіть проміжки на яких функція набуває додатніх значень.
6. Укажіть проміжки на яких функція набуває від’ємних значень.
7. Укажіть проміжок, на якому функція зростає.
8. Укажіть проміжок, на якому функція спадає.

 

                 Відповіді

Варіант 1.  1. а˃0.  2. (-1;-9).  3. х= - 1.  4. -4; 2.  5. (-∞;-4); (2;+∞).

6. (-4; 2).  7. [-1; +∞).  8.  (-∞; -1].  9.  с<0.  10.  b>0.

 

Варіант 2.  1.  а<0.  2.  (-1;9).  3.  х=-1.  4.  -4; 2.  5.  (-4;2). 

6.  (-∞;-4); (2;+∞). 7.   (-∞; -1].  8.  [-1; +∞).  9.  с>0.   10.  b<0. 

 

2. Записати рівняння графіка функцій. (слайд 9)     

 

3.. Побудувати квадратичну функцію (робота в групах)

                           y=x²-4x-5; (слайд 10,11)     

Вказати вершину параболи, нулі функції, напрям віток параболи, вісь симетрії, проміжки зростання і спадання.                         

           4. Встановити відповідність між графіками функцій та формулами. (слайд 12)     

5. Робота в групах.

 

                                       Гімн Параболі(Відео)

 

               6. ЗАСТОСУВАННЯ ПАРАБОЛИ. (слайд 13)     

Квадратична функція або її графік, парабола, дуже часто зустрічається в різноманітних галузях науки і виробництва. Ви стоїте на порозі вибору свого життєвого шляху. Профілізація старшої школи передбачає три основні напрямки – технологічний, природничо-математичний і гуманітарний. Тому, можливо, декому з вас здасться, що з квадратичною функцією та її графіком ви не будете більше зустрічатись.

Хоча у геометрії квадратичною функцією виражається залежність площі квадрата від його сторони, площі круга від його радіуса тощо. У фізиці – це, наприклад, залежність пройденого шляху від часу при прямолінійному рівноприскореному русі.

В астрономії парабола також зустрічається. Відомо, наприклад, що якщо космічному кораблю чи штучному супутнику, який обертається навколо Землі, надати другу космічну швидкість, то його траєкторія руху перетвориться з еліптичної в параболічну, і він зможе покинути Землю.

Інженерні розрахунки показують, що різні споруди, мости, арки у формі параболи мають підвищену міцність.

Я хочу переконати вас втому, що параболи, розташовані навколо нас, для цього достатньо лише придивитись.

Учень 1.        Оптичні властивості параболічних дзеркал.

До наших днів дійшла легенда про те, як Архімед збудував увігнуті дзеркала і за їх допомогою спалив римські кораблі. Більшість вчених відкидають цю легенду, оскільки такі дзеркала повинні були би мати надто великі розміри, а при тодішньому розвитку техніки це було неможливо.

Але навіть, якщо історія про спалення кораблів є легендою, то все ж таки спалити римський флот з допомогою параболічних дзеркал можливо.

Результати, які отримав Архімед, ґрунтувалися на такому твердженні: будь-яка пряма, паралельна осі симетрії параболи, після відбиття від параболи проходить через її фокус. Для того, щоб збудувати дзеркало, що збирає сонячні промені в одній точці, потрібно відшліфувати його по параболоїду обертання. Параболоїд – це поверхня, яку можна одержати, якщо обертати параболу навколо своєї осі.

Якщо спрямувати таке параболічне дзеркало на Сонце, то всі відбиті промені пройдуть через фокус параболи, і температура в фокусі виявиться настільки великою, що з допомогою сонячних променів можна буде закип’ятити воду, розплавити свинець і інше. Звідси й походить назва ”фокус”, що на латині означає “вогнище”.

 

 

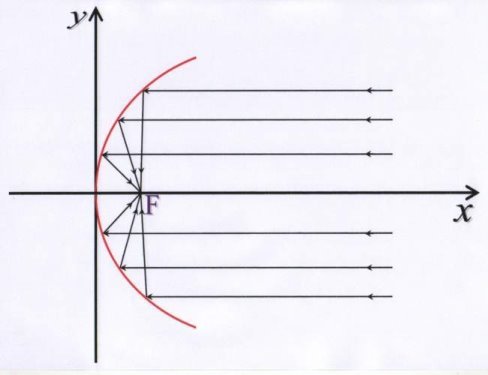
Учень 2.                    Парабола і військова справа. (слайд 14)     

 

Траєкторією руху снарядів цікавилися багато вчених, особливо з моменту винайдення пороху в ХІІІ столітті. Жодне укріплення не могло довго витримати артилерійську стрільбу. Пізніше здогадалися застосовувати навісну стрільбу, яка дозволяла стріляти із-за укриття.

Щоб забезпечити точне попадання, потрібно було вивчити рух тіла, кинутого під кутом до горизонту. Вчені довели, що таке тіло рухається по параболі.

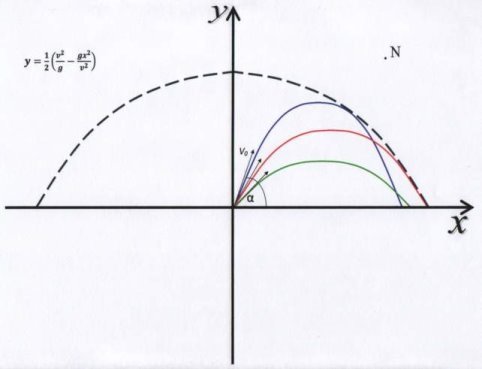
Якщо при заданій початковій швидкості снаряда змінювати кут α, то одержуємо нескінченну кількість парабол. Всі параболи, для яких            45˚ < α < 90˚, дотикаються до одної і тої ж лінії, рівняння якої 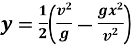                   . Її називають параболою безпеки.

Якщо точка N знаходиться поза областю, що обмежується цією параболою, то при початковій швидкості v снаряд не потрапить у точку N при жодному куті нахилу.

 

 

 

 

 

 

 

 

 

 

 

 

VІІ. ПІДВЕДЕННЯ ПІДСУМКІВ.

 

 

VІ. Підсумок уроку Ми з вами сьогодні дуже плідно попрацювали. Молодці! (слайд 15)     

Дякую за роботу сумлінну та відповідальну,

спасибі за працю і вміння, такт і спілкування.

 

 

V. ПОСТАНОВКА ДОМАШНЬОГО ЗАВДАННЯ.

-Д,С,Р, №2 ,с.109,1-6 3. (слайд 16)     

За бажанням, пропоную виконати творче завдання – написати реферат, час на написання рефератів – тиждень.

Творче завдання

• Тема № 1: “Функція. Квадратична функція, цікаві властивості  параболи.”
• Тема № 2: “Квадратична функція в задачах промислового та сільськогосподарського змісту.”
• Тема   №    3: “Ода параболі.”
• Тема   №    4: “Квадратична функція у фізиці”